磁浮管道物流系统智能测速算法研究

程浪 ，杨杰 ，丰富 ，高涛，齐洪峰，邵福波

(1.江西省磁悬浮技术重点实验室，江西 赣州 341000；2.中国科学院 赣江创新研究院，江西 赣州 341000；3.中车工业研究院有限公司，北京 100076)

永磁悬浮管道物流系统[1]采用永磁悬浮技术，可实现“零功率”悬浮，依托综合管廊进行物流运输，安全高效，不占用地面空间，发展潜力巨大。永磁悬浮管道物流系统模型如图1所示。测速定位技术[2]是管道物流运输系统的关键技术，对于物流运输系统的安全预警、运行控制、运输效率具有重要意义。目前常采用多普勒雷达实现永磁悬浮管道车辆速度测量，并对速度数据进行积分得到列车的位移。但雷达信号设备易受强磁场干扰[3]、气流冲击、车辆振动以及信号覆盖角移位等问题的影响，导致量测噪声的统计特性发生变化，且易产生远大于或小于列车真实运行速度的失常数据[4]。随着发车间隔[5]的不断压缩，以及列车编队技术的需要，对列车测速定位技术的测量精度以及安全性方面提出了更高的要求。基于最优估计理论的数据滤波、融合处理，降低了因传感器缺陷所导致的误差，从而提升测速定位的性能[6]。卡尔曼滤波是一种基于最优估计理论的优化算法，它可以通过分析带有噪声和扰动的输入数据对系统的状态进行最优估计[7]。在实际应用中，量测数据的噪声统计特性易受复杂工况影响发生变化，使得常规卡尔曼滤波算法受到极大限制。Saga-Husa 自适应滤波算法可以对噪声的统计特性进行实时估计和调整[8]，在量测噪声统计特性发生变化时依然能够实现最优估计，但存在计算量较大和容易发散等缺点[9-10]。针对此类问题，文海平等[11]提出一种基于新息检测的自适应抗差卡尔曼滤波算法，该算法通过引进抗差因子和自适应因子对量测噪声协方差矩阵和状态预测协方差矩阵进行调整，提高了组合导航的精度。王广玉等[12]利用残差协方差对量测噪声统计特性进行实时修正，进而调整卡尔曼滤波增益，获得更好跟踪效果。孙旭等[13]采用一种极大后验噪声估计器对量测噪声进行在线修正，避免系统发生滤波发散的问题，并减小了量测噪声的估计误差。石青[14]利用自适应卡尔曼滤波器的残差信息结合模糊推理系统得出位置和姿态调节因子，对滤波器的噪声统计特性进行在线修正，解决量测噪声变化不规律的问题。针对复杂工况下测速数据的量测噪声统计特性发生变化的问题，本文以永磁悬浮管道物流系统的测速定位技术为研究背景，提出一种新型Sage-Husa自适应滤波算法，在Sage-Husa自适应滤波算法的基础上进行简化，并引入模糊推理系统，对量测噪声协方差进行在线修正，同时设置了失常数据判定阈值，对失常数据进行补偿，进一步提高滤波器的速度估计精度，通过仿真及实测车载数据对传统卡尔曼滤波、Sage-Husa 自适应滤波以及新型Sage-Husa 自适应滤波算法进行对比，验证了新型Sage-Husa 自适应滤波算法具有更高的速度估计精度及对失常数据的补偿能力。

图1 永磁悬浮管道物流系统Fig.1 Permanent magnet suspension pipeline logistics system

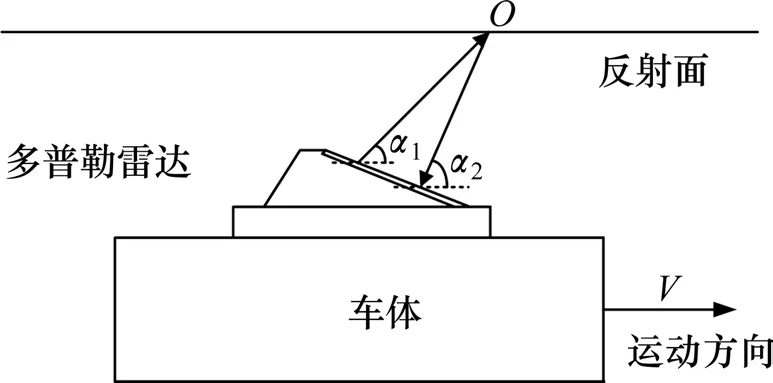
图2 多普勒雷达测速原理示意图Fig.2 Schematic diagram of Doppler radar velocity measurement

1 多普勒雷达测速原理

多普勒雷达以多普勒效应为基础，通过检测发射波与回波之间的频率信号差来计算列车相对于地面的速度值[15]，可实现无接触式速度测量[16]，为永磁悬浮管道物流系统的测速定位问题提供了技术参考。

设车体行驶速度为V，雷达发射波频率为fT，发射波与水平方向夹角为α1，反射波与水平方向夹角为α2，电磁波速度为c，则根据多普勒效应，测速反射面O接收到的电磁波频率为：

雷达接收到的回波频率为：

将式(1)代入式(2)可得：

回波与发射波之间的频率信号差为：

从而在知道多普勒雷达发射波频率fT并检测到发射波与回波之间的频率信号差fe的条件下即可求出当前车体速度V：

以图1为实验样车，多普勒雷达安装在永磁悬浮管道物流系统运输车体的顶部，采集小车速度数据。永磁悬浮管道物流运输系统测速示意图如图3所示。

图3 管道物流运输系统测速示意图Fig.3 Schematic diagram of speed measurement of pipeline logistics transportation system

选取管轨小车速度v与位移s作为系统的状态变量，X=[v,s]T，设管道内小车以初速度为v0=0 m/s，加速度为a，采样时间间隔为Δt，k时刻系统的运动学方程如下：

系统的状态方程与量测方程如下：

2 Sage-Husa 自适应滤波算法及其改进

2.1 Sage-Husa自适应滤波算法及改进方案

Sage-Husa 自适应滤波算法是一种基于极大后验噪声统计估值器的自适应滤波算法[17]。其在卡尔曼滤波算法的基础上，通过传感器获取的数据和系统的先验估计值对系统噪声和量测噪声统计特性在线修正，以解决噪声变化不规律的问题。

Sage-Husa自适应滤波算法如下。

先验估计：

先验误差协方差：

残差计算：

卡尔曼增益：

后验估计：

后验误差协方差：

系统噪声均值：

系统噪声协方差：

量测噪声均值：

量测噪声协方差：

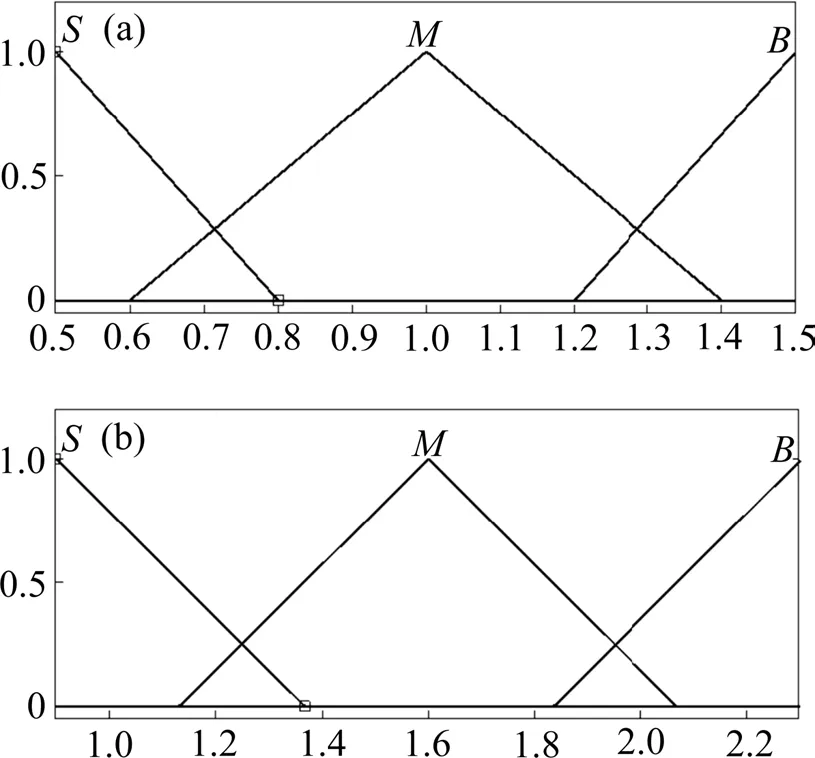
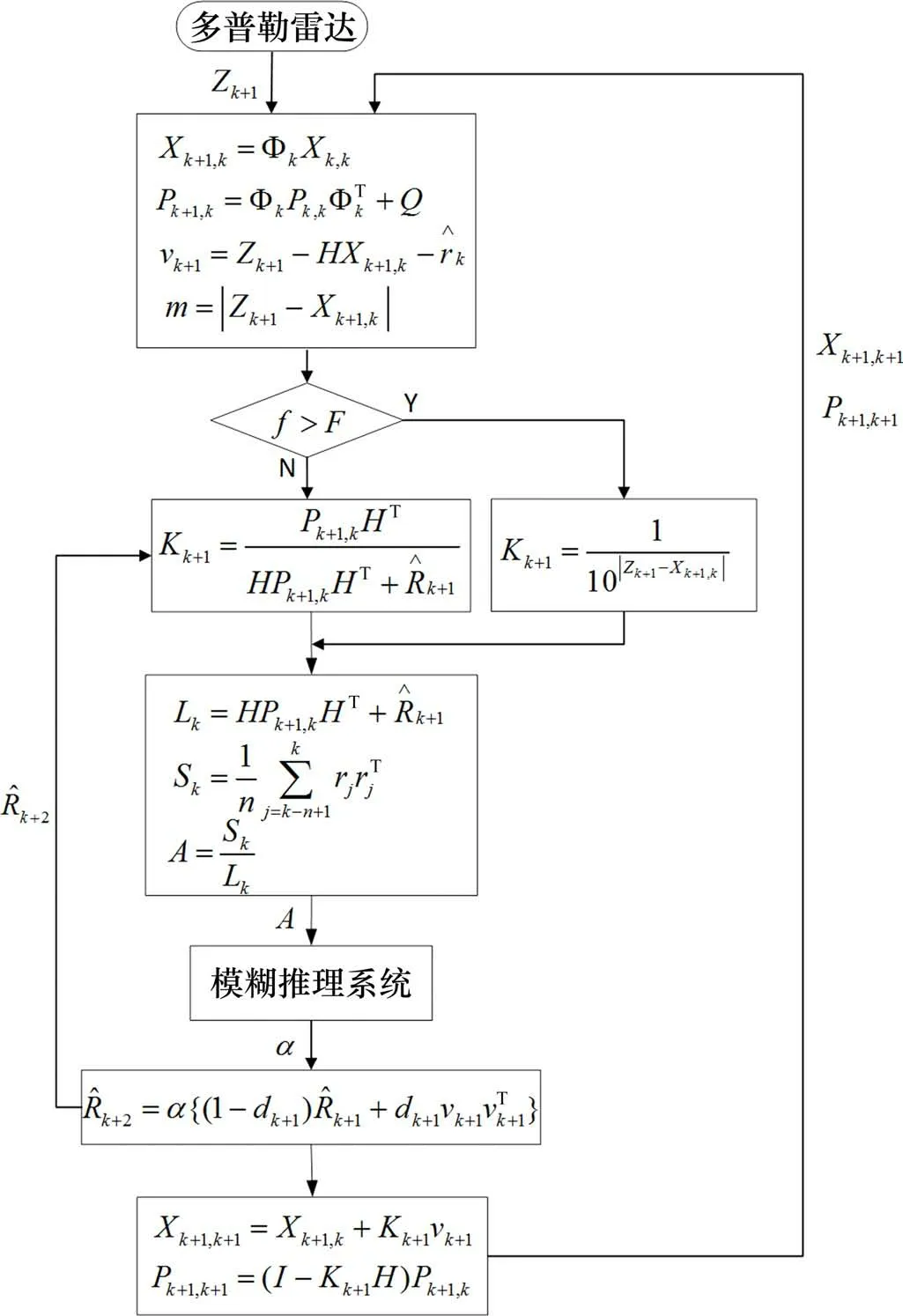
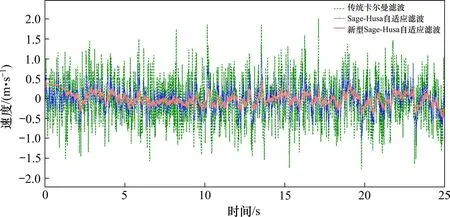
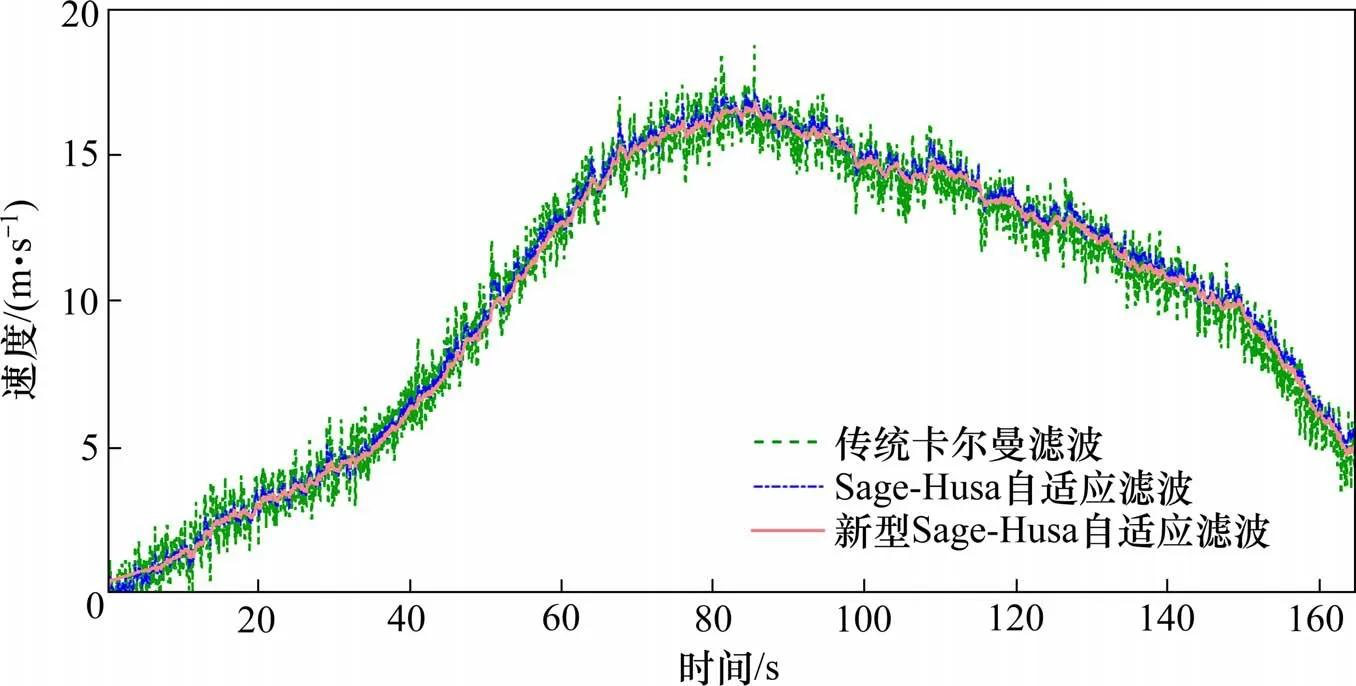
式(8)～式(17)中，Φk为状态转移矩阵，为系统噪声协方差矩阵，Zk+1为k+1 时刻的量测值，+1为量测噪声协方差矩阵，H为量测矩阵，dk(0

Sage-Husa 自适应滤波算法虽然可以对噪声统计特性进行实时修正，但其算法运算量也相应增加，同时在滤波过程中易发生发散的问题[18]。因而，对Sage-Husa 自适应滤波算法做如下改进：

1) Sage-Husa 自适应滤波算法不能同时对系统噪声协方差阵和量测噪声协方差阵进行估计[19]。故采用先验信息给出的初始设定值Q作为系统噪声协方差阵，不进行自适应修正，对算法进行简化，以减小运算量。即去掉式(14)与式(15)，并对式(8)与式(9)分别修改为：

2) 采用量测噪声协方差阵的渐进无偏估计对其进行简化，并引入模糊调节因子α对量测噪声进行调节，实现对量测噪声协方差阵的实时修正。此时式(17)成为

模糊推理系统以残差协方差的实际值和理论值之比A作为输入量，调节因子α为输出量作用于量测噪声协方差，对进行实时修正。

3) 针对多普勒雷达测速过程中可能产生的失常数据，设置失常数据判定阈值F，当量测值与系统状态预测值差值的绝对值f小于阈值F，则认为量测数据是正常数据，卡尔曼增益K仍按式(11)计算；当f超过阈值F，则认为量测数据大概率是失常数据，此时应自适应调节卡尔曼增益K，式(11)改为：

式(21)中，当量测值与系统状态预测值之间差值越大，卡尔曼增益K将呈指数级减小，此时对量测数据的干预程度也就越强，分配给量测值的权值也就越小，相应的分配给状态预测值的权值越大，系统估计值就越不相信量测值，越偏向于状态预测值，从而实现对量测失常数据的补偿。

2.2 引入模糊推理系统

当多普勒雷达在理想工作状态下进行测速时，设定好噪声参数的卡尔曼滤波器能够滤除测量噪声的干扰，实现对速度的最优估计。但当多普勒雷达在复杂的工况下运行，导致系统的量测噪声统计特性发生变化与设定的噪声参数不匹配时，传统卡尔曼滤波器难以预测出小车的真实速度。因此，在量测噪声统计特性发生变化时，需要对卡尔曼滤波器的量测噪声参数进行自适应调节以匹配真实的量测噪声状况。选取n个时刻的实际残差rk，求出其均值rˉ和方差Sk，如下所示：

残差协方差理论值Lk：

模糊系统的输入A：

式(22)～(25)中，Hk为量测矩阵，Pk+1,k为先验误差协方差矩阵，量测噪声协方差矩阵。

模糊控制以残差实际方差和理论方差的比值A为输入量，量测噪声调节因子α为输出量，当A偏离1 时，通过调节因子α调整可以改变Lr的大小，从而使A回到1附近。定义模糊子集M表示在1 附近，B表示大于1，S表示小于1。A的论域为[0.5,1.5]，α的论域为[0.9,2.3]，根据经验与仿真调试构建模糊规则表[20]，模糊控制规则可表示为：

A和α的隶属度函数如图4所示。

图4 模糊推理系统输入输出的隶属度函数Fig.4 Membership function of input and output of fuzzy reasoning system

新型Sage-Husa 自适应滤波算法流程可描述为通过多普勒雷达获取量测数据Zk+1，同时根据系统上一次后验估计Xk,k，Pk,k计算系统的先验估计Xk+1,k和Pk+1,k，并计算残差vk+1和量测值与系统状态预测值差值的绝对值f；通过失常数据阈值判定计算出对应的卡尔曼增益Kk+1，然后计算残差协方差的实际值与理论值之比A，将其作为模糊控制系统的输入，得到模糊控制系统的输出α，对量测噪声协方差进行在线调节，最后得出系统的后验估计Xk+1,k+1和Pk+1,k+1，并更新为下一次先验估计的输入。

新型Sage-Husa 自适应滤波算法流程框图如图5所示。

图5 新型Sage-Husa自适应滤波算法流程框图Fig.5 Flow block diagram of the new Sage-Husa adaptive filtering algorithm

3 实验分析

3.1 联合仿真模型

本文在Matlab/simulink 仿真软件中，采用SFuction 函数模块实现新型Sage-Husa自适应滤波程序开发，采用Fuzzy 模块构造模糊控制算法，并搭建基于新型Sage-Husa 自适应滤波器、传统卡尔曼滤波器和Sage-Husa 滤波器的仿真模型。通过仿真获取测速数据，对数据施加设定的量测噪声，将其作为3种卡尔曼滤波器的量测信号输入，分别通过3种滤波器得到各自的系统预测值输出，同时当前得到的系统预测值也将作为下一次滤波更新各自系统的先验估计值输入。

仿真模型框图如图6所示。

图6 仿真实验模型框图Fig.6 Block diagram of simulation experiment model

3.2 结果对比与分析

设定系统噪声Q=0.2 初始量测噪声R=0.2，仿真实验初始条件：加速度a=0.5tm/s2，初速度v0=0 m/s，施加=5R的高斯白噪声，3 种卡尔曼滤波器的仿真速度数据如图7所示。

图7 仿真速度对比Fig.7 Comparison diagram of simulation speed

仿真速度误差对比如图8所示。

图8 仿真速度误差对比Fig.8 Comparison of simulation speed errors

仿真速度最大误差对比如图9所示。

图9 仿真速度最大误差对比Fig.9 Comparison of maximum error of simulation speed

从图7 和图8 中可以看出，当实际量测噪声大于系统设置量测噪声时，传统卡尔曼滤波不能较好地跟踪真实数据，精度及平稳性都较差，新型Sage-Husa自适应滤波效果最好，Sage-Husa自适应滤波器次之。从图9 可知，3 种卡尔曼滤波器的估计速度与实际速度最大偏差依次为2.25，1.17 和0.64 m，最大误差率依次为12.3%，6.39%，1.42%，相比于传统卡尔曼滤波器、Sage-Husa 自适应滤波器，新型Sage-Husa 自适应滤波器精度分别提高10.88%和4.97%。

针对测速数据失常情况，对仿真数据施加随机的突变干扰，并设置实际量测噪声协方差=5R，使用3 种卡尔曼滤波仿真失常速度数据如图10所示。

图10 仿真失常速度对比Fig.10 Comparison of simulation aberration velocity

仿真失常速度误差对比如图11所示。

图11 仿真失常速度误差对比Fig.11 Comparison of simulation aberration velocity errors

仿真失常速度最大误差对比如图12所示。

图12 仿真失常速度最大误差对比Fig.12 Comparison of maximum error of simulation abnormal velocity

从图10 和图11 中可以看出，传统的卡尔曼滤波器无法剔除失常数据的影响，Sage-Husa 自适应滤波器虽然对失常的量测数据有一定的补偿作用，但是估计值无法快速收敛到真实值附近，且失常数据与真实值之间差值过大时，会导致Sage-Husa自适应滤波的发散。而新型Sage-Husa 自适应滤波器能够很好地剔除失常数据的影响，且能够较快地收敛到真实值附近。

由于磁浮管道物流系统仍处于研发阶段，尚不具备实验条件，本文选在悬浮原理及驱动方式与磁浮管道物流系统类似且技术成熟的“红轨”上进行测速实验。“红轨”属于中低速永磁磁浮轨道交通试验线，线路全长800 m，载客能力88 人，最高设计运行速度80 km/h[21]。设定程序系统噪声Q=0.2，初始量测噪声R=0.2，对速度数据施加=5R的高斯白噪声，输入3种卡尔曼滤波器中进行仿真，得到的实测车载速度对比如图13所示。

图13 实测车载速度对比Fig.13 Comparison of actual vehicle speed

实测车载速度误差对比如图14所示。

图14 实测车载速度误差对比Fig.14 Comparison of actual vehicle speed errors

实测车载速度最大误差对比如图15所示。

图15 实测车载速度最大误差对比Fig.15 Comparison of the maximum error of actual vehicle speed

从图13 和图14 中可以看出，在实际车载数据实验中，相较于前2 种滤波算法，新型Sage-Husa自适应滤波器依然保持了很好的估计精度与平稳性，从图15可知，3种卡尔曼滤波器的估计速度与实际速度最大偏差依次为2.4，1.2 和0.68 m，最大误差率依次为14.6%，7.9%，4.3%，相比于传统的卡尔曼滤波器和Sage-Husa 自适应滤波器，新型Sage-Husa 自适应滤波器精度分别提高10.3%和3.6%。通过实测车载测速数据滤波实验进一步验证了新型Sage-Husa 自适应滤波算法的优越性。

4 结论

1) 针对管道物流运输系统多普勒雷达测速定位模块在复杂工况中量测噪声统计特性变化及数据失常的问题，提出一种新型Sage-Husa 自适应滤波算法。该算法对Sage-Husa 自适应滤波算法进一步优化，通过引入模糊推理系统对量测噪声的增益系数进行调节，实现对量测噪声的实时修正；通过失常数据判定阈值调节卡尔曼增益，实现对失常数据的补偿。

2) 搭建仿真模型对新型Sage-Husa 自适应滤波器进行验证，在给定实际量测噪声=5R，数据正常的情况下，传统卡尔曼滤波器、Sage-Husa 自适应滤波器，新型Sage-Husa 自适应滤波器的最大误差率依次为12.3%，6.39%，1.42%，与前2 种卡尔曼滤波器相比，新型Sage-Husa 自适应滤波器精度分别提高10.88%和4.97%；在数据失常的情况下，相较于前2 种卡尔曼滤波器，新型Sage-Husa自适应滤波器能够很好地剔除失常数据的影响，且能较快收敛到真实值附近。

3) 采用实测车载数据对新型Sage-Husa 自适应滤波算法进一步验证，传统卡尔曼滤波器、Sage-Husa自适应滤波器和新型Sage-Husa自适应滤波器的最大误差率依次为14.6%，7.9%和4.3%，与前2种卡尔曼滤波器相比，新型Sage-Husa 自适应滤波器精度分别提高10.3%和3.6 %，进一步验证了新型Sage-Husa 自适应滤波算法具有更高的精度和对失常数据的补偿能力，对于提高磁浮管道物流运输系统测速定位技术的精度和可靠性具有重要的学术意义，同时，本方法对其他轨道交通制式的测速定位也具有重要的参考价值。