基于Gabor 滤波的并行网络无参考图像质量评价

李国涛，杨忠，张驰，朱傥，许昌亮

南京航空航天大学 自动化学院，江苏 南京 211106

在过去的几年里，随着计算机和互联网技术的发展速度大大加快，多媒体技术的发展也有较大的进步。然而，在多媒体系统中，数字图像在采集、处理、压缩、存储和传输等过程中存在的失真会导致图像质量的下降[1]。因此，在图像处理领域中，对一张图像的质量进行评分已然成为一个关键的课题研究。

图像质量评价（ image quality assessment，IQA)可用于如图像去噪、图像重建、图像合成和视频编码等许多图像处理应用当中。根据利用参考图信息的情况，IQA 分为全参考（full-reference）、半参考（reduced-reference）和无参考（no-reference）3 种类型[2]。其中，第3 种无参考的图像质量评价(no-reference image quality assessment， NR-IQA)算法是最具有广泛适用性的，原因是实际应用中往往没有无失真的图像可供全参考或半参考的算法作为参考。

早期的NR-IQA 方法利用从图像中提取的一些基于经验观察的特征[3-6]来评价图像质量，但这种方法效果一般，这就表明了这些手工特征存在着一定的局限性。而深度学习方法可以使用卷积层来提取图像的特征，然后利用全连接层将特征映射到质量分数[7-9]。Kang 等[10]提出的IQA_CNN利用卷积神经网络获取图像特征，并将图像分割成若干图像块来训练模型从而实现图像质量评价。Liu 等[11]提出RankIQA 对网络进行训练之前，首先对失真图像集的质量进行了排序，才用于网络的训练，然后为了训练更深的网络，利用了迁移学习技术。通过生成图像这一方式，RankIQA模型可以实现训练数据的增加。由于NR-IQA 没有参考图作对比，Ren 等[12]提出的RAN4IQA 首先生成未失真的原图，然后用类似全参考的评价方式获得质量分数，即利用了生成式对抗网络(generative adversarial networks，GAN)的思想，也取得了不错的效果。Su 等[13]提出了一个自适应网络架构的hyperIQA，该方法为了提取图像的深层语义特征，用到了ResNet50 网络，然后利用超网络建立起感知规则，该感知规则又被应用于质量预测网络。Yan 等[14]虽然也提出用2 个分流网络来增强对图像特征的提取，取得了一定的效果，但是由于其将图像分割成32×32 的小图像块而过多忽略了整体图像本身所含有的信息，且为了反映图像结构而使用的梯度图在失真程度较弱时变化不明显，因此存在一定的局限性。

基于以上分析，考虑到图像质量评价数据集的数据量不充足以及图片失真非均匀性的问题，本文针对无参考图像质量评价的问题提出了一种基于Gabor 滤波的并行网络深度学习算法，并在LIVE 和TID2013 数据集上进行实验，以证明该算法的有效性。

1 图像预处理

考虑图像的失真可能存在着非均匀性，即在输入图像的不同部分中，失真类型和失真程度通常会有所不同。针对该问题，本文利用可提取空间局部频域特征的Gabor 滤波器[15]来获取边缘图片。同时，针对图像数据量的不足，采取图片切块的方式增大数据量以便深度神经网络的训练学习。因此，在网络训练之前，要对图片进行边缘图像的获取以及切块的预处理。

1.1 基于二维Gabor 滤波器的边缘图像获取

Gabor 滤波器实质上是一种小波。早在1946 年，一维Gabor 函数便由英国物理学家Gabor 率先提出。直到1980 年，将Gabor 的一维形式扩展到二维[16]才被DAUGMAN 提出。通过设置不同的参数，Gabor 滤波器可以在不同尺度、不同方向上的进行滤波，能有效地提取图像的边缘特征，感知纹理信息。文献[17]中的生物研究表明，哺乳动物大脑皮层存在着用于实现视觉机制的感受细胞，而Gabor 小波也具有这样的性质，这和NR-IQA 领域追求质量评分与人类视觉系统一致的目的有了共同的特性。由复正弦波调制的椭圆高斯包络线组成的二维Gabor 滤波器，不仅对输入图像局部区域的频率有着一定的敏感程度，对空间频率也有着一定的敏感性。Gabor 函数表达式如下：

式中：

实数部分表达式为

虚数部分表达式为

不同的Gabor 参数生成的滤波器不同。本文各参数取值如下： λ为滤波器波长，取值为3； θ为滤波器方向，取值范围是0～π； ψ为正余弦因子参数的相位偏移，取值为0； σ为Gabor 函数的高斯因子标准差，取值为1.5； γ为空间纵横比，取值为1.2。

从图1 和图2 可以看出，未失真图片在经过Gabor 滤波器之后，获得的边缘特征更为细致，而失真图像的边缘特征相对来说就缺失了许多，这就说明了Gabor 滤波对图像失真引起的边缘损失比较敏感。

图1 失真图及其边缘图

图2 未失真图及其边缘图

1.2 图像切块

获取灰度图和边缘图片后，考虑深度神经网络的训练需要充足的数据量，对图像进行切块处理，且一张图上切块形成的多张新图像块的对应质量分数也取原图像的分数，以此达到增强数据集的目的。同时为了保证原图像的每一部分都能够作为切块后的数据集使用，并且切块后的图像相互之间没有重叠的部分。那么，切块图像的尺寸大小应该是原图像长宽的公约数，所以切块后的尺寸设为128×128。图像切块方式如图3 所示，若一个数据集的图像大小为384×384，经切块处理得到128×128 大小的图像块，可使得整体数据量扩为原来的9 倍，便于深度网络的训练学习。

训练完成的模型对一张图片进行分数预测时，整张图像的质量分数是取其所有图像块分数的平均值，公式如下：

式中：q为预测图片的分数，Np为该图像切割的图像块数，xi、gi分别为输入图像块的灰度图与边缘图，f为由图像块xi、gi到质量分数q的映射关系。

2 并行网络结构

本文旨在通过一个并行网络来学习视觉外观与图像质量间的复杂关系。目前，大多数的NRIQA 方法只是使用图片的灰度图像或者RGB 图像作为输入。相比之下，本文考虑了大多数失真可能导致图片边缘结构信息损失的问题，在以灰度图片为输入的分支网络主要学习图像各像素的强度等特征的同时，也利用另一个分支网络去重点学习边缘图像的结构特征。由于边缘图像更能反映图片中高频分量由于失真导致的损失情况，如此一来，利用并行网络学习到的多重融合的特征则更能反映图像质量的情况，再回归预测后得到的分数也就更贴合人类的视觉感知。

2.1 特征提取网络

本文的特征提取网络是选取改进后的VGG16。为了在提高网络拟合能力的同时，进一步减少参数，经典的VGG16 网络[18]采用了多个较小卷积核（3×3）的卷积层来增加非线性映射的数量，但是其要求输入图片大小224×224，而本文图像块大小为128×128。因此，本文只采用VGG16网络前面的图像特征提取部分。

本文的特征提取网络结构如图4 所示。该网络共包含了13 个卷积层和5 个最大池化层，针对输入128×128 大小的图像块，充分提取其图像特征，最终得到图4 中4×4×512 的图像特征。

2.2 回归预测网络

针对并行的特征提取网络获得的多重融合的特征，需要将其映射到与人的视觉感观相一致的质量分数。NR-IQA 并行网络结构如图5 所示，针对特征提取网络从灰度图像块和边缘图像块获得的2 个4×4×512 的特征量，将其扩展成2 个1×1×8 192的特征向量后，分别各自通过1 个8 192×512 的全连接层获得2 个1×1×512 的特征向量，将2 者连接起来形成1 个1×1×1 024 的特征向量；然后经过1 个1 024×256 的全连接层，得到1×1×256 的特征向量；最后经过256×1 的全连接层，获得最终的图像质量预测分数。

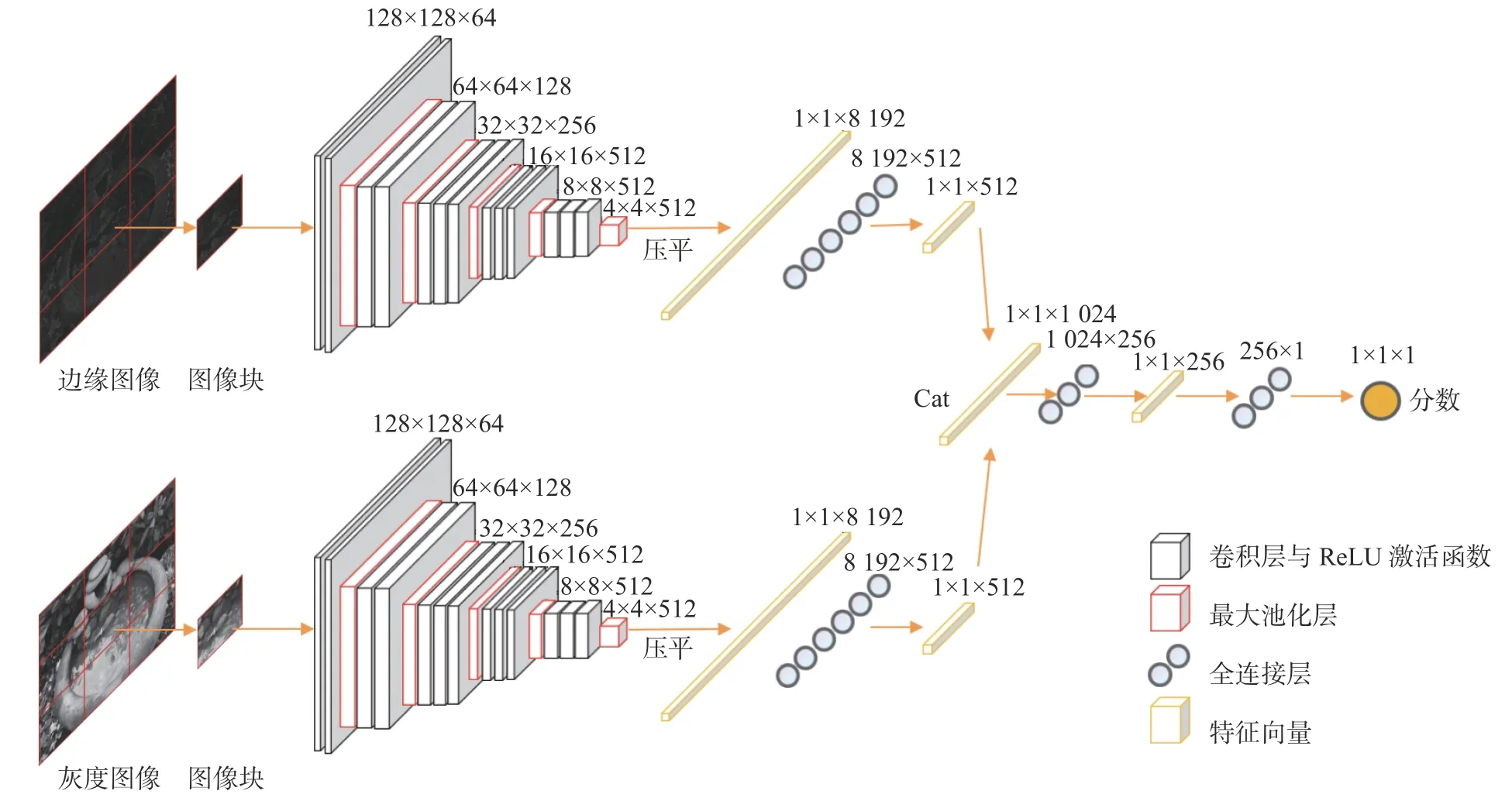
图5 NR-IQA 并行网络

3 实验结果与数据分析

本节将所提出的NR-IQA 并行网络算法在公开数据集LIVE[19]和TID2013[20]上进行实验来验证其有效性。

3.1 数据集与评估指标

数据集LIVE 共包含779 张失真图像，大多数图像大小为768×512，这些失真图像是由25 张未失真图像经过5 种不同类型失真在不同失真级别上所生成的，所有图像质量的平均意见得分（direrential mean opin-ion score，DMOS）都在一个[0,100]范围，如图6 所示。其中DMOS 越高，表示失真程度越高，也就说明图像质量越低。数据集TID2013 共有3 000 张失真图像，大多数图像大小为512×384，这些失真图像是由25 张原始图像通过非偏心图像噪声、压缩失真（如JPEG）等24 类不同失真所形成的，如图7 所示。每张图像的平均意见得分（mean opin-ion score，MOS）值都在[0,9]内，其中较低的MOS 表示失真程度较高，也就说明图像质量越低。

图6 LIVE 数据集图像

图7 TID2013 数据集图像

评价指标采用了用于评价模型预测准确性的斯皮尔曼秩相关系数（Spearman rank order coefficient，SROCC）、评价单调性的皮尔森线性相关系数（Pearson linear correlation coefficient，PLCC）、评价相关一致性的肯德尔秩次相关系数（Kendall rankorder correlation coefficient，KROCC）和评价偏差程度的均方根误差（root mean squared error，RMSE）。其中，SROCC 和PLCC 这2 点指标最为重要，两者取值范围均为[0,1]，值越接近1，表明模型效果与人眼主观视觉的一致性越好。

3.2 实验配置

本文实验平台的配置如表1 所示。

表1 实验平台相关配置

根据平台硬件设备性能，本实验将训练集与测试集比例设为8∶2，网络输入图像大小设为128×128，将网络训练的批尺寸(batch size)、迭代次数(epoch)和初始学习率（learning rate）分别设为32、150 和0.000 1，更新一次学习率的步长（step size）为30，更新学习率的乘法因子（gamma）为0.9。

3.3 消融实验

利用所提出的基于Gabor 滤波的并行网络NR-IQA 算法在LIVE 数据集上进行消融实验，以证明使用128×128 的图像块作为输入、采用边缘图像的并行网络以及利用Gabor 滤波获取边缘图像这3 点对图像质量预测是积极有效的。

实验数据如表2 所示。消融实验一共分为4 组，分别为：1）G_Net_128：表示采用128×128 大小的灰度图像块作输入的单分支网络模型；2）GS_PNet_128：表示采用128×128 大小的灰度图像块和经Sobel 算子所获得的边缘图像块作为输入的并行网络模型；3）GG_PNet_32：表示采用32×32 大小的灰度图像块和经Gabor 滤波所得的边缘图像块作为输入的并行网络模型；4）作为本文提出的GG_PNet_128：表示采用128×128 大小的灰度图像块和经Gabor 滤波所得的边缘图像块作为输入的并行网络模型。

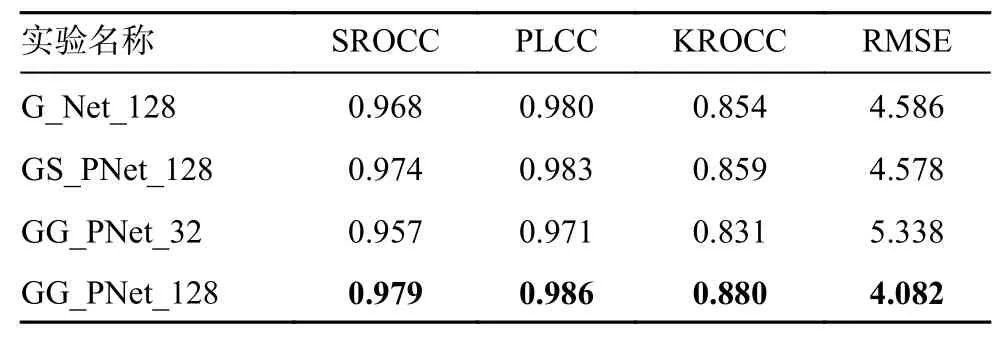
表2 在LIVE 数据集上的消融实验

从表2 实验结果可知，采用本文所提算法的第4 组实验GG_PNet_128 在4 个指标上均获得了消融实验中最好的数值，这也证明了在本文所提算法中这3 点改进均使得模型效果与人眼主观视觉的一致性得到了提升。

实验GG_PNet_128 的训练曲线如图8 所示。由图8 中的Loss 曲线可以看出，网络训练过程中较快地达到了收敛，并且较为平稳。

3.4 对比实验

这一节选择了基于深度学习的代表性算法在LIVE 数据集和TID2013 数据集上的性能表现来做对比实验，如DIQaM-NR[9]、DIIVINE[5]、CORNIA[21]、BIQI[4]、RankIQA[11]、hyperIQA[13]等算法，实验结果如表3 所示。

由表3 实验结果可知，在LIVE 数据集和TID2013 数据集上，本文所提算法都基本取得最好的效果，虽然在LIVE 数据集上的SROCC 指标比RankIQA 小了0.002，但是在TID2013 数据集上的SROCC 指标却高出其0.88。

要评估一个算法的好坏，算法的泛化能力也是一个很重要指标，为了评估模型性能，本文以SROCC 作为主要指标，并与以下多种经典算法进行比较：如BRISQUE[22]、BLIINDS-II[23]、DIIVINE[5]、CORNIA[21]和DIQaM-NR[9]。将在LIVE 数据集上训练的模型放在TID2013 数据集上进行测试，以及将TID2013 数据集上训练得到的模型放在LIVE 数据集上进行测试，实验结果如表4 所示。

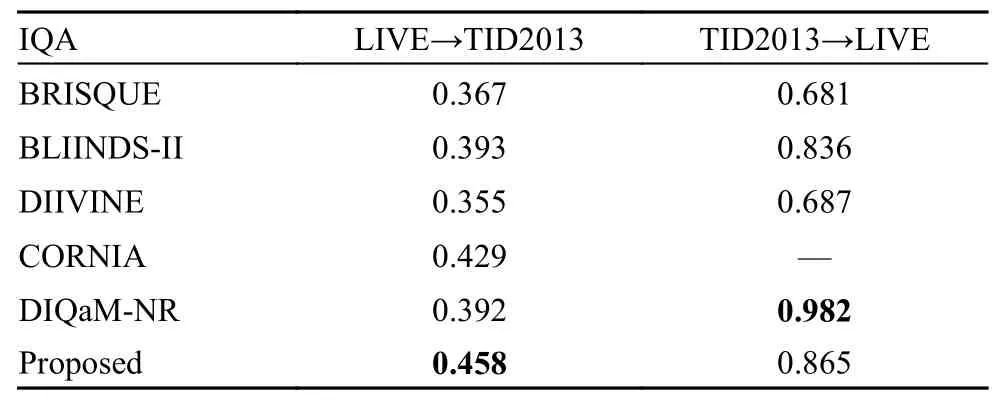
表4 跨数据集性能评估的SROCC 指标

由表4 实验结果可知，LIVE 上训练的模型在TID2013 数据集上的测试效果明显不佳，而TID2013 上训练的模型在LIVE 数据集上的测试效果明显较好。这是因为LIVE 数据集只有5 种失真类型，而TID2013 数据集却有24 种失真类型。那么在数据更丰富且失真类型更多的TID2013数据集上进行训练，所得模型自然泛化能力也要更优秀。

在LIVE 数据集上，以SROCC 为评价指标，针对数据集单一失真类型进行本文算法与主流算法的性能对比实验，如DIIVINE[5]、BRISQUE[22]、NIQE[6]、HOSA[24]、MCNN[25]、BIECON[26]。实验结果如表5 所示。

由表5 实验结果可知，在LIVE 数据集中的5 种失真类型里，在JP2K、WN、BLUR 和FF 这4 个失真类型图像上的质量预测均取得最优异的效果，而JPEG 这一失真类型图像上的质量预测也仅次于BIECON。

4 结束语

本文提出了一种基于Gabor 滤波的并行网络无参考图像质量评价算法，该算法通过增加一个输入大小为128×128 边缘图像的分支网络提取图像质量特征，一定程度上弥补了以灰度图像输入的单支网络提取图像质量特征不足的缺陷；同时，可提取空间局部频域特征的Gabor 滤波器也在一定程度上解决了图像失真非均匀性导致的质量评价不准确的缺陷。实验结果也表明所提算法的图像质量评分与人类主观视觉有较高的一致性。由于不同的失真有着不同的特性，图像的失真类型也是多样且复杂，因此，提高NR-IQA 算法的通用性是今后的研究重点。