基于独立分量相异性分析的动态过程监控研究
张成,李明业,潘立志,李元
1. 沈阳化工大学 理学院,辽宁 沈阳 110142
2. 沈阳化工大学 信息工程学院,辽宁 沈阳 110142
随着现代化工和生物企业生产技术的发展,企业对生产过程的安全性和可靠性提出了越来越多要求。近年来,多元统计过程监控(multivariate statistical process monitoring, MSPM)方法被广泛应用于生产过程的安全状态监控,并取得了令人满意的结果[1-2]。在一些工业生产过程中,首先,MSPM根据正常的历史数据建立过程监控模型,然后生产操作人员可以根据上述训练阶段计算出的控制限,对当前的生产过程进行正常或故障的决策。
众所周知,主成分分析(principal component analysis, PCA)是一种重要的多元统计分析过程监控方法,并已被用于监控某些生产过程中的状态[3]。需要注意的是,当主成分分析用于监控工业过程时,监控数据必须遵循多元高斯分布[4]。然而,大多数研究表明,不同生产过程中的数据是非高斯分布[5],非高斯分布降低了PCA 的过程监控性能。为了解决非高斯分布的数据,提出了独立分量分析(independent component analysis, ICA)方法[6]。与PCA 相比,ICA 不仅降低了高阶统计相关性,而且可以提取监控过程中的非高斯信息[7]。Lee 等[8]提出了基于ICA 的统计过程监控方法,并使用2 个统计量来监控非高斯过程的状态:I2和SPE (squared prediction error)。本质上,ICA 是一种静态统计策略,这意味着ICA 只考虑不同变量之间的相关性,而忽略了不同样本之间的自相关和滞后相关对过程检测的影响。然而,一些研究表明,在大多数化工过程中,动态特性是显著的。为了克服动态过程中的非高斯问题,Lee等[9]提出了动态独立分量分析(dynamic independent component analysis, DICA)。当DICA用于监控过程状态时,分别提取样本和变量的自相关和互相关[10-11]。在进行故障检测时,DICA 同样采用 I2和SPE 进行过程监控。 I2和SPE 统计量主要评估样本在子空间中的分布变化,而通常忽略样本在时间上的变化。有研究表明,在DICA 中计算出的统计量仍然具有显著的自相关,这意味着一些故障样本无法根据控制限进行识别[9]。为了考虑样本在时间上的变化信息,Kano 等[12]定义了一个相异指数,利用相应特征值之间的差异定量评估正常和故障条件之间的分布差异。之后,Wang 等[13]提出一种相异指数分析的多变量渐进式诊断方法,并将其应用于连续过程。Zhao 等[14]提出了基于相异指数分析的移动窗口间歇过程监控并将相异指数应用于非线性过程。研究表明,相异指数方法能够快速、有效地提取数据在时间上的变化信息即自相关性并能作为一个新的统计量进行故障检测。
针对DICA 在动态过程中捕获的独立分量存在自相关性和统计量存在漏报的问题,本文提出一种基于独立分量相异性分析(DICA dissimilarity analysis, DICA-DISSIM) 的动态过程状态监控研究。为了实现对动态过程的监控,在DICA 的基础上引入了相异指数。本文方法能有效地处理独立分量子空间中样本之间的自相关性,减少动态特性对故障检测的影响。
1 动态独立分量分析
假设观测数据X=[x1,x2,···,xm]T∈Rm×j(m为样本个数,j为变量个数),ICA 可以从原始数据X中估计出混合矩阵A和 独立分量S[8]。
在DICA 中,首先建立增广矩阵,其公式为
式中l为滞后参数。接下来在矩阵X中实现ICA。其目的是求出解混矩阵W,然后计算重构后的独立分量S,计算公式为
详细的过程主要包括白化和计算独立分量。
在动态独立分量分析中,主要通过白化来消除监控变量的互相关。
式中:Q为白化矩阵, Λ和U为特征分解所得。
求解独立分量S和解混矩阵W的计算公式为
为了估计矩阵B,使用了FastICA 算法[6]。
最后,DICA 监控指标的计算公式为
式中:sd=WdxT,Wd可以由W的行范数进行排序并根据行范数贡献率选取[10],且Bd表示 B中对应的前 d列。
2 基于独立分量相异性分析的的动态过程状态监控研究
2.1 相异指数
混合数据集X=[X1;X2]∈Rm×j(m=m1+m2)的协方差矩阵为R,通过特征分解得到特征值的对角矩阵 Ω和特征向量V,最后建立1 个新的变换矩阵P。
将数据集Xi转换为Yi,计算其协方差矩阵Ci,最后计算出特征值和特征向量。
最后,监控指标D作为统计量,其计算公式为
相异指数D在0~1 变化。一些研究表明,当数据集彼此十分相似时,D接近0;反之,当数据集彼此具有差异时,D接近1[12]。
2.2 基于独立分量相异性分析的动态过程状态研究
DICA 方法可以提取独立信号,但需要注意的是,在复杂的动态过程中,提取的独立分量含有显著的自相关性,这将导致一些显著的故障无法被检测。此外,在DICA 中,监控指标 I2统计量的控制限为圆形度量,故 I2统计量存在漏报的问题。
接下来将通过一个简单的动态数值例子进行验证DICA 的统计量存在的问题。例子模型为
式中w1(k)=2sin(0.02kπ),w2(k)∼U(-2,2),对z进行监控。
首先由例子模型分别生成1 组训练数据和1 组故障数据。其中,训练数据中的2 000 个样本为正常,测试数据的前1 000 个样本为正常,后1 000个样本在w的第1 个变量上添加幅值为4 的阶跃故障。图1 给出独立分量的散点图,其中,训练数据外部的圆代表 I2控制限。在该数值例子中,阶跃故障设置较大,而由图1 可以看出,控制限内的故障数据无法被检测出,这意味着使用圆形控制限监控独立分量时,故障检测率较低。除此之外,DICA 捕获的独立元还具有较强的自相关性,如图2。
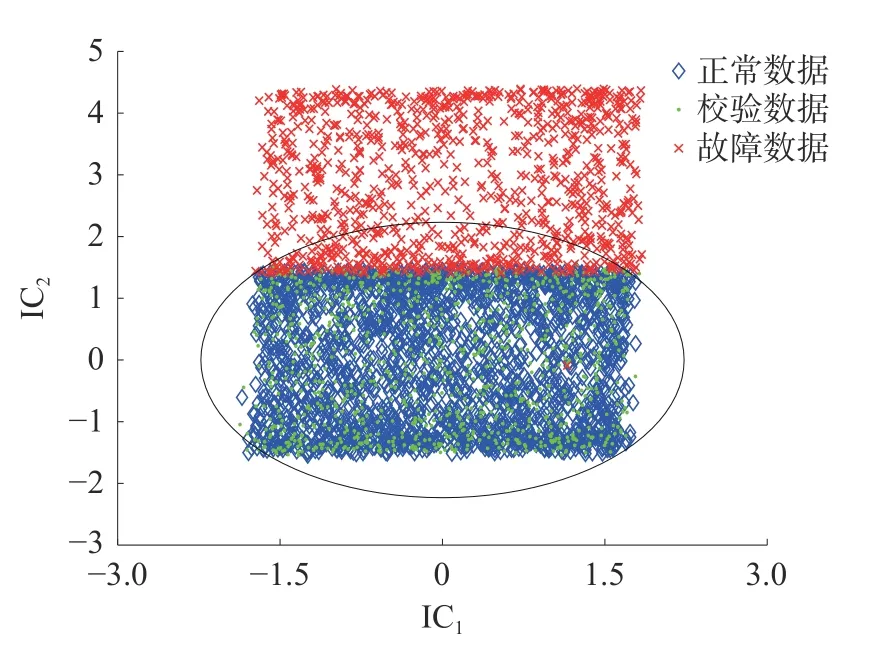
图1 IC 子空间中样本的散点图
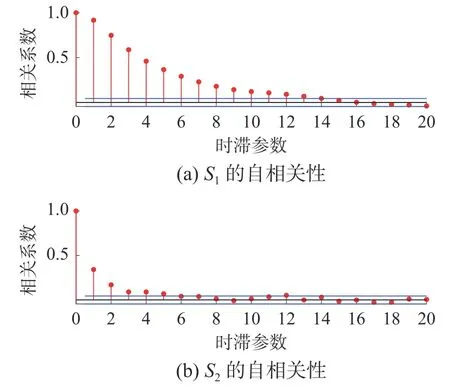
图2 独立分量的自相关性图
基于上述分析,本文提出了一种基于独立分量相异性分析的研究,用于监控动态过程的状态。
首先采集2 组正常数据集X1,X2∈Rm×j,构造2 组正常数据的增广矩阵L1,L2∈R(m-l)×j(l+1),通过动态独立分量分析算法得到独立分量S(1),S(2)。
式中:l为 时滞参数,m-l为样本个数,d为独立分量个数。
为了实现过程监控,在独立分量子空间引入滑动窗口。设窗宽为w,步长为h,第i个窗口公式为
式中i=1,2,···,(m-l-w)/h+1。
混合数据集可以表示为
将混合数据进行相异性分析,并计算其协方差矩阵,最后进行特征分解得到特征值 λ(1)。
为了监控过程状态,由式(1)分别求出训练数据和测试数据的监控指标D和Df。最后,使用核密度估计法(kernel density estimation, KDE)[15]按照99%的置信度确定控制限DUCL,通过比较Df和DUCL确定故障检测结果。
独立分量相异性分析的动态过程监控方法故障诊断过程主要包括离线建模、在线检测和故障诊断3 个步骤。
1)离线建模
①构造2 组训练数据X1,X2的增广矩阵L1,L2;
②利用L1的均值和方差对L1,L2标准化处理,记为,;
③根据ICA 得到L¯1的解混矩阵Wd和独立分量S(1),同理得到的独立分量S(2);
④根据滑动窗口技术 ,依次在S(1)和S(2)上选取窗口数据和,然后计算相异指数D,最后使用核密度估计法确定控制限DUCL。
2)在线检测
①采集第k窗口数据集,并构造增广矩阵F(k);
②利用L1的均值和方差对F(k)进行标准化,记为;
⑤若>DUCL,则F(k)为故障样本,否则,F(k)为正常样本。
3)故障诊断
由于协方差矩阵的特征值代表主分量的方差,设主分量为Gd,则有
式中:Id为单位矩阵I的第d个列向量,P为转换矩阵。若记则可表示成
式中为F(k)的第i列。
则每个独立分量的贡献为
最后,各监控变量的贡献的计算公式为
需要注意的是:本文方法并不是简单的将DICA 与相异指数结合。DICA 方法可以通过白化降维和获取数据的动态信息,但是无法彻底解决数据中样本之间存在的自相关性,并且 I2统计量的控制限存在一定的局限性,对检测结果造成很大影响。相异指数方法考虑了样本在时间上的变化信息,但是无法快速提取有用的信息。因此,本文在DICA 的基础上引入相异指数,能够有效地处理DICA 捕获的独立分量的自相关性,该方法还解决了DICA 统计量存在漏报的问题。最后,本文提出了一种基于贡献图的故障诊断方案,该方案解决了相异指数方法无法通过控制图找出故障的问题。
3 仿真实验
3.1 数值例子
将DICA-DISSIM 的故障检测与诊断方法用于文献[16]中的动态数值例子。具体数值例子模型为
式中w(k)为-2~2 均匀分布的二维随机向量,对u和y进行监控。
首先由数值例子模型生成1 组训练数据和1 组故障数据。训练数据中的1 000 个样本为正常,测试数据的前300 个样本为正常,后700 个样本在w的第1 个变量上添加幅值为2 的阶跃故障。
使用ICA、DICA、Diss(dissimilarity)和本文方法对此动态过程进行模拟。在本文方法中,通过交叉验证选择窗宽和步长,最后将窗宽设为75,步长选取为1。其中,DICA 和本文方法中的时滞参数l=2,根据核密度估计方法将检测方法的置信度定为99%。
当在动态数值例子中使用ICA 时,检测结果如图3 所示。ICA 去除了变量之间的线性相关性,但在动态过程中,ICA 捕获的独立分量具有较强的动态性,导致故障检测率较低。
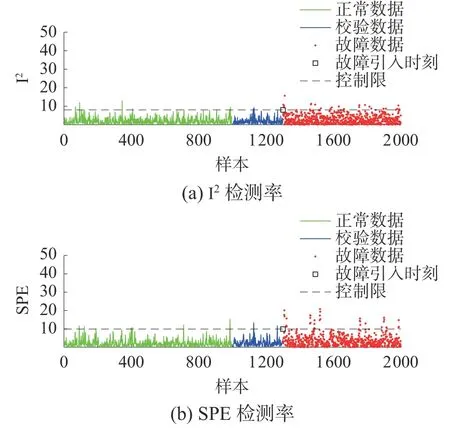
图3 ICA 故障检测结果
当在动态数值例子中使用DICA 时,如图4、5 所示,DICA 在白化中去除了变量之间的线性关系和样本之间的动态性,但捕获的独立分量还存在一定的自相关性,并且由本文2.2 节分析可知DICA 统计量的控制限无法检测出部分故障,所以DICA 的故障检测率较低。DICA 的故障检测结果如图6 所示。使用相异指数分析动态数值例子时,故障检测结果如图7 所示。

图4 DICA 的2 个独立分量
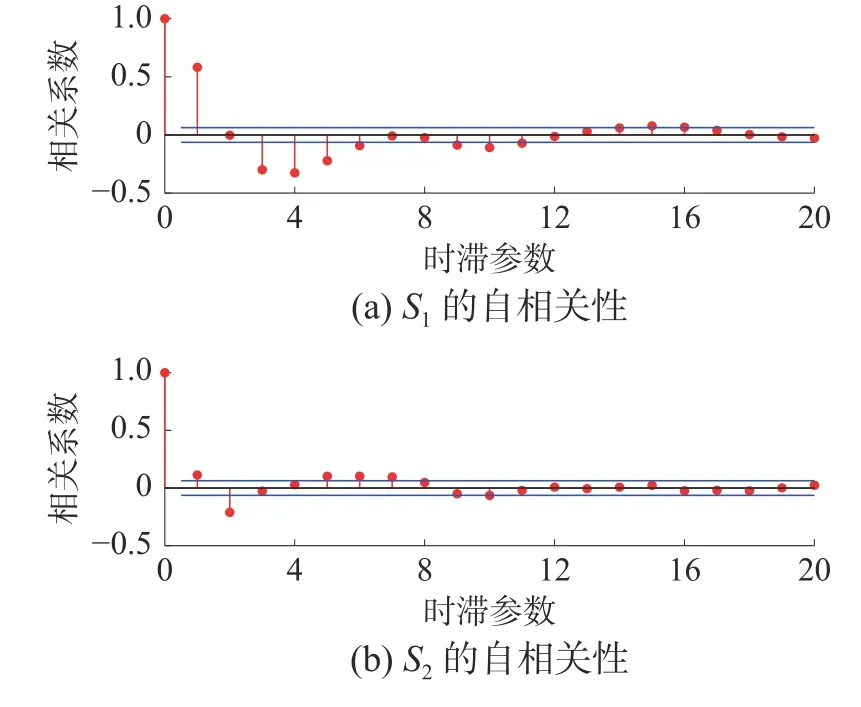
图5 独立分量的自相关性图
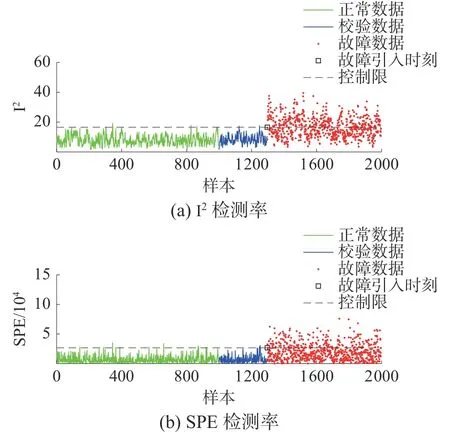
图6 DICA 故障检测结果
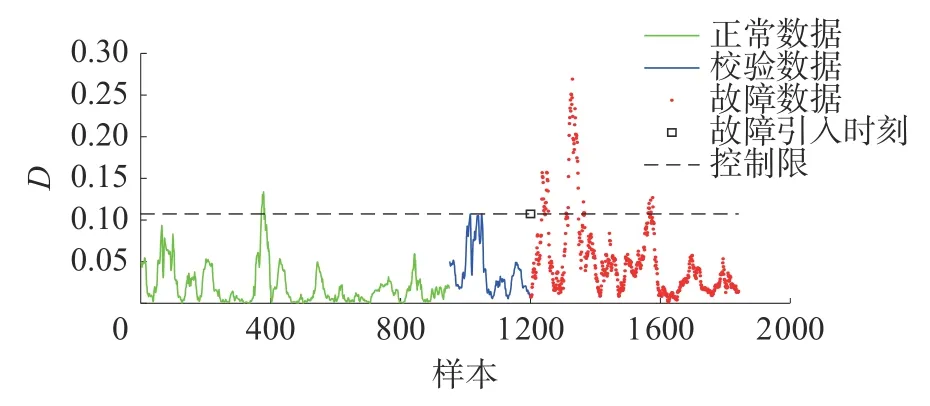
图7 Diss 故障检测结果
当在动态数值例子中使用本文方法时,通过DICA 得到独立分量,在独立分量中引入相异指数D,既能捕获数据的动态特征又能消除独立分量的自相关性,并为新统计量来量化数据之间的差异。因此,本文方法比传统的ICA、DICA 监控指标I2、SPE更适用于动态过程的监控,检测结果如图8 所示。可以看出本文方法的故障检测率明显高于传统的ICA、DICA 和相异指数方法。
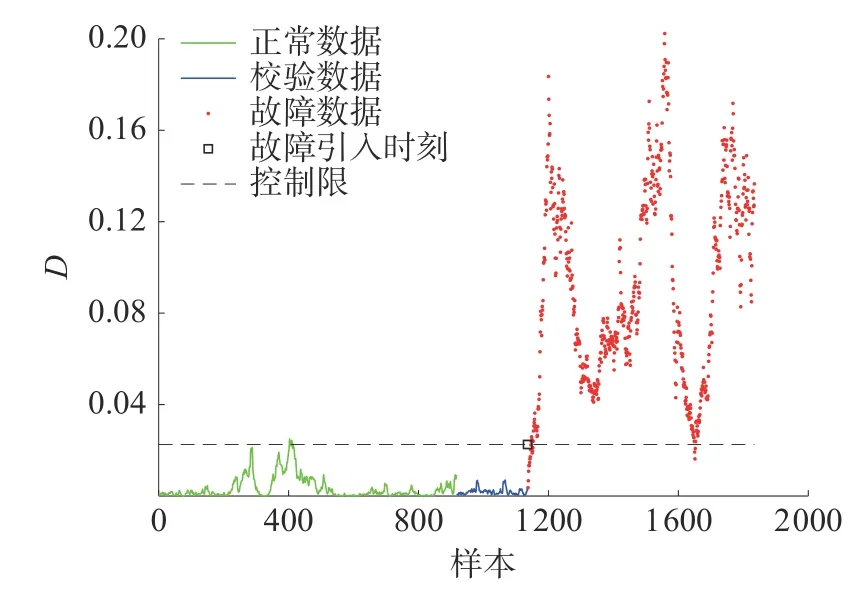
图8 本文方法故障检测结果
最后,对动态数值例子进行故障诊断。测试数据每一个变量对统计量D的贡献度如图9 所示。由图9 可知,变量4 的贡献度最大,其次是变量1,即故障主要由第1、4 个变量引起。
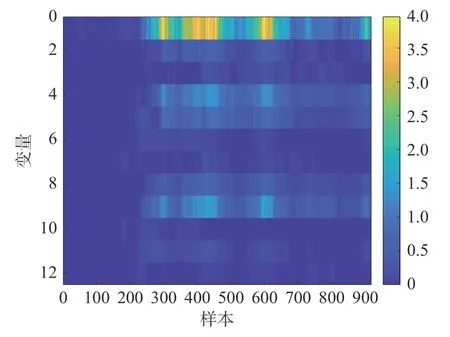
图9 监控变量贡献
在该数值例子中,监控了u1、u2、y1、y2共4 个变量。由于在w的第1 个变量上添加了故障,通过本文所提出的故障诊断方法可知,故障在变量y2上体现最明显,其次是变量u1。在图10 中,绿色部分代表训练数据,蓝色部分代表校验数据,红色部分代表故障数据,可以看出第1 个变量u1和第4 个变量y2中的故障数据向上偏移,这与本文方法的诊断结果一致。

图10 监控变量
3.2 田纳西-伊斯曼仿真过程
田纳西-伊斯曼(tennessee-esatman,TE)过程是一个被广泛应用于过程监控领域的仿真平台,该过程主要是模拟实际工业过程[17-18]。TE 过程如图11 所示,包括5 个主要操作单元,该过程将4 种反应物送入反应器,产生2 种产物和1 种副产物。
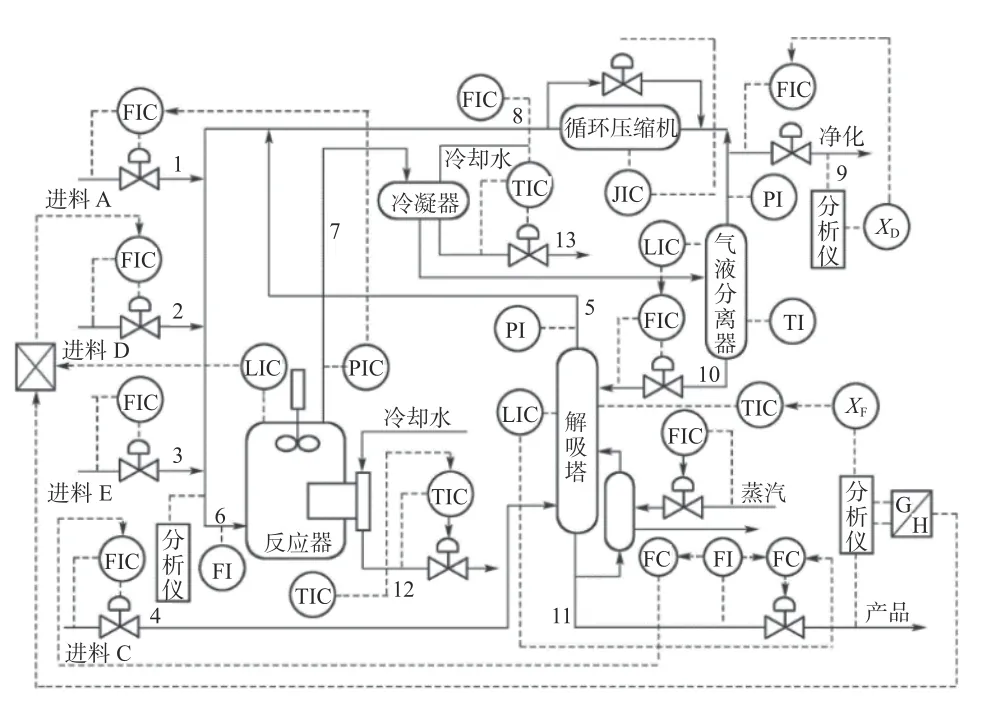
图11 TE 过程
本节中仿真数据由TE 仿真器使用模态1 生成。将TE 仿真器中时间参数设置为10 h,采样周期为0.01 h。在该过程中,采集了1 000 个正常样本作为训练数据。对于测试数据,收集28 个故障数据集,每个数据集1 000 个样本,所有故障都是在第300 个样本后引入。
对于在线故障检测,本节中ICA 和DICA 按照文献[8]负熵规则选取2 个独立分量。在本文方法中,通过交叉验证确定窗宽选取为75,步长选取为1。其中,DICA 和DICA-DISSIM 中的时滞参数l选取1,对第12 组测试数据集分别使用ICA、DICA 和DICA-DISSIM 方法进行测试,检测结果分别如图12~14 所示。通过比较4 种方法的检测结果,可以得到本文方法能检测出故障12 的发生,并且本文方法的故障检测率最高。表1 给出了每组测试数据使用ICA、DICA、动态主成分分析(dynamic principal component analysis, DPCA)和DICA-DISSIM 方法进行故障检测的结果。

表1 TE 过程中各方法的故障检测率
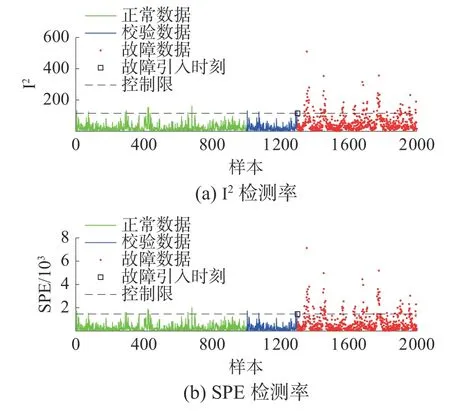
图12 ICA 故障检测结果

图13 DICA 故障检测结果
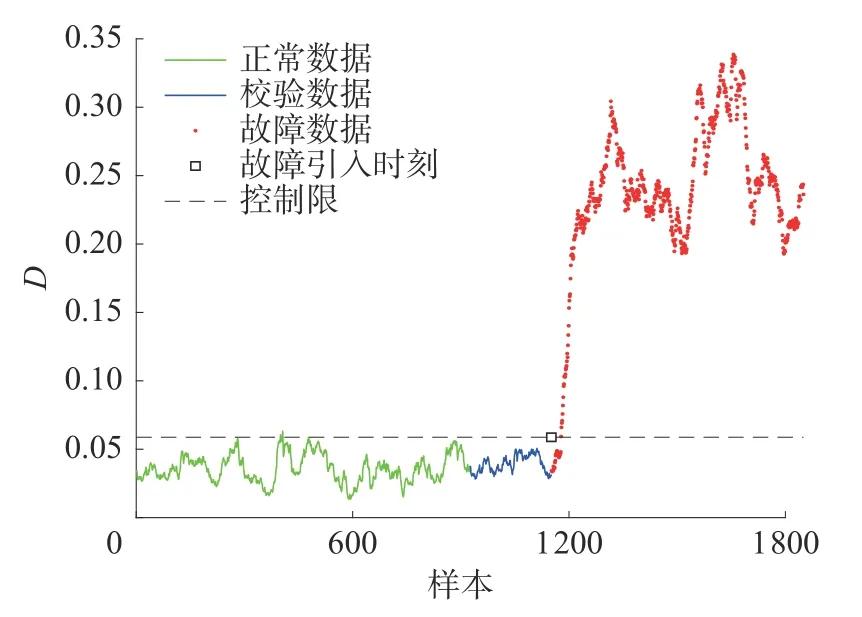
图14 本文方法故障检测结果
使用本文方法对故障5 进行诊断。如图15所示,前50 个变量是样本当前时刻的变量,后50 个变量是样本前一时刻的变量。从图15 可以看出,变量50 的贡献最大。如图16 所示,变量50 在第300 个样本之后出现震荡。对故障15 进行诊断,如图17 所示,变量9、22 和49 贡献较高。另外,从图18 可以看出变量9、22 和49 在第300 个样本之后出现了较大的偏移。综上所述,故障5 和故障15 的诊断结果与实际相符,验证了所提诊断策略的正确性。
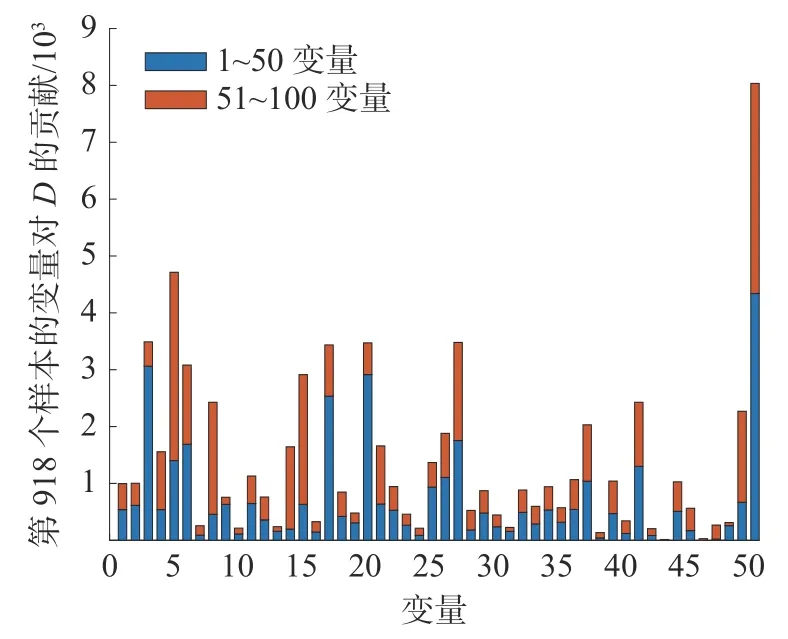
图15 故障5 的贡献图
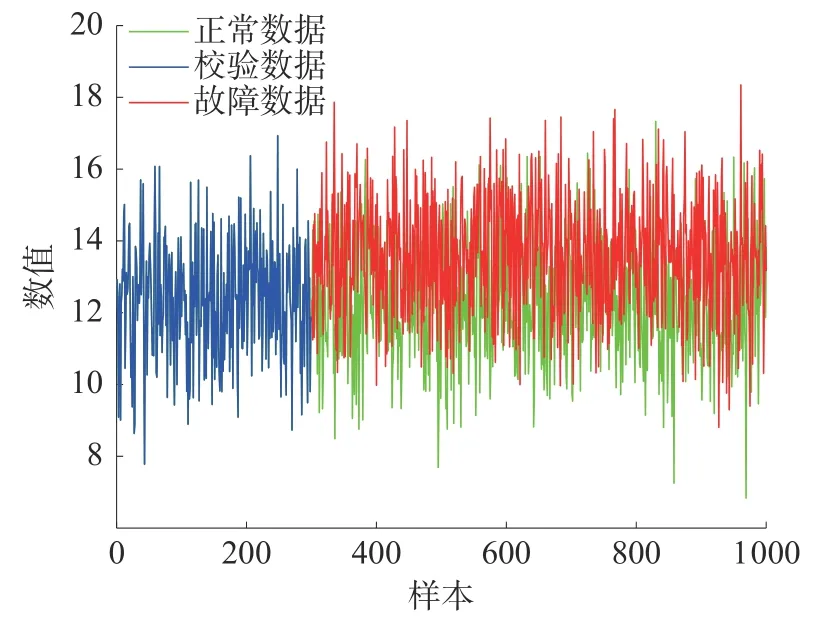
图16 故障5 的变量50

图17 故障15 的贡献图
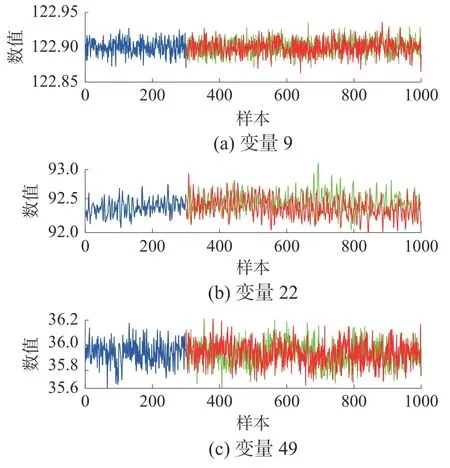
图18 故障15 的变量9,22,49
经上述分析,本文提出方法在动态过程监控中具有更好的检测性能。
4 结束语
针对动态独立元分析在动态过程中捕获的独立分量存在自相关性和统计量漏报的问题,提出一种基于DICA 相异性分析的故障检测与诊断方法。该方法通过DICA 与相异指数结合,能够有效处理上述问题。本文通过动态数值例子和田纳西-伊斯曼过程进行仿真测试,仿真结果表明所提方法相对于ICA 和DICA 有效提高了故障检测率。
本文方法在动态过程的故障检测中效果较好,接下来可以研究的方向是在非线性动态过程中,独立元空间引入相异指数是否有效,能否处理非线性动态数据。

