基于Workbench的活塞式空压机护盖网可靠性分析

林思桥，叶小龙，朱汉城，陈 虹

(厦门东亚机械工业股份有限公司，福建 厦门 361100)

1 引言

活塞式空压机VA-80运用于轨道交通场合，安装与列车底部。空压机工作时，护盖网不仅受到来自空压机本身的激振，还会受到列车运行过程随机振动所产生的激振[1-2]。可见，相比于工作于普通厂房的空压机，运用于轨道交通的活塞式空压机VA-80的工作条件更为严峻复杂，需要具有更为优秀的抗振性能[3]。活塞式空压机VA-80的护盖网链条网采用点焊连接，角件与底部横梁没有满焊，需要对护盖网的强度及振动烈度进行评估。

活塞式空压机VA-80的护盖网网面为链条网，边缘与网罩边框及底部横梁点焊连接。护盖网底部由2个角件点焊到网罩框架上，角件与底部横梁采用角焊固定，护盖网与活塞式空压机本体通过2个角件的腰孔采用螺栓固定。为了验证活塞式空压机VA-80的护盖网可靠性，本文将利用有限元分析方法，对护盖网进行稳态结构分析、模态分析和随机振动分析。

2 护盖网可靠性分析原理

2.1 应力场的计算理论

基于弹性力学和有限元的理论[4-8]，空间单元的基本方程为

[k]e{q}e={F}e

(1)

单元内部的位移为

(2)

单元内部的应变为

{ε}e=[B]e{q}e

(3)

单元内部的应力为

{σ}e=[D]{ε}e

(4)

式中 [k]e——单元刚度矩阵

[N]——形函数矩阵

[B]e——单元应变矩阵

[D]——弹性矩阵

2.2 模态分析的计算理论

多自由度系统的自由振动运动方程和其自由振动解[9-11]可以表示为

(5)

x=Asin(ωt+φ)

(6)

式中M——系统的质量矩阵

K——刚度矩阵

A——振幅矢量

ω——无阻尼固有频率

φ——相位角

将式(6)代入式(5)中可以得到齐次代数方程组

(K-ω2M)A=0

(7)

定义振型系数φi为第i阶阵型矢量Ai中各个元素与最大值的比值，则由式(1)可以得到n个固有频率ωi和固有振型φi。

2.3 随机振动分析的计算理论

由模态分析的结果，可以得到系统一般振型的坐标方程[12-14]

(8)

x=φX

(9)

式中X——振型坐标

φ——振型矢量矩阵

fi(t)——广义力

对式(8)两边做傅里叶变换，可以得到振型坐标的频响函数

(10)

将Hi(ω)组成的对角矩阵表示为Hdiag(ω)，则传递矩阵函数可以表示为

H(ω)=φHdiag(ω)φT

(11)

振型坐标X和物理坐标x的谱密度函数矩阵可表示为

(12)

(13)

由此可以得到系统输出响应的相关函数矩阵

(14)

3 护盖网模型介绍

本文所分析的活塞式空压机VA-80护盖网的三维模型如图1所示，整体分为5个部分，分别为链条网、角件、底部横梁、网罩边框以及焊缝。焊缝长度和位置根据工艺及设计图纸确立，模型中焊缝长度为25 mm，位于2个角件和底部横梁的连接处。网罩边框材质为Q235A，其余材质均为Q235B。两种材质的力学性质如表1所示。

表1 护盖网材料力学性能

图1 护盖网三维模型

活塞式空压机VA-80护盖网的网格模型如图2所示，网格的节点总数为340759，单元总数为162707。针对所关注的焊缝区域，加密该处网格，焊缝区域的网格模型如图3所示。

图2 护盖网网格模型

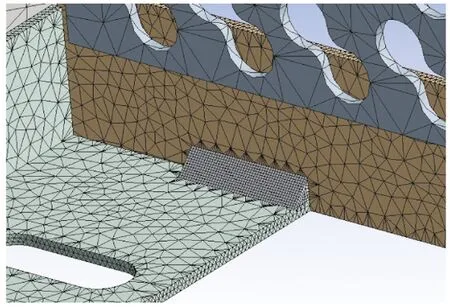
图3 焊缝网格模型

4 稳态结构分析

4.1 边界条件设置

根据护盖网的设计图纸、制造工艺以及护盖网实际的安装固定方式，本文对护盖网的边界条件进行了合理的简化，具体边界条件设置如下：

(1)链条网点焊连接：链条网边缘与网罩框架、底部横梁的连接处均施加点焊连接，位置分布如图4所示；

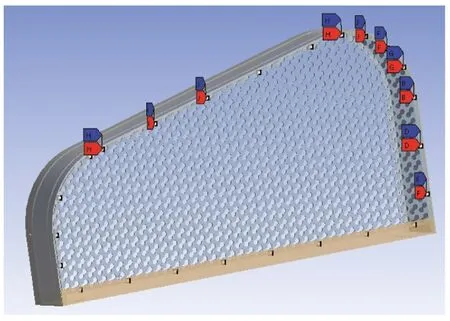
图4 链条网点焊位置分布

(2)角件点焊连接：2个角件与网罩框架施加点焊连接，位置分布如图5所示；

图5 角件点焊位置分布

(3)固定约束：2个角件底面施加固定约束；

(4)重力载荷：整体施加一个竖直方向的重力载荷。

4.2 稳态结构分析结果

施加上述边界条件后，稳态结构分析计算得到护盖网的位移和应力结果，如图6和图7所示。由图可见，护盖网的最大位移位于网罩边框顶部，其值为5.98×10-5mm；最大等效应力位于网罩边框右侧的内边缘，其值为3.87 kPa。护盖网在稳态情况下，仅受重力及固定约束，位移和应力均处于一个较小值，结构稳定可靠。

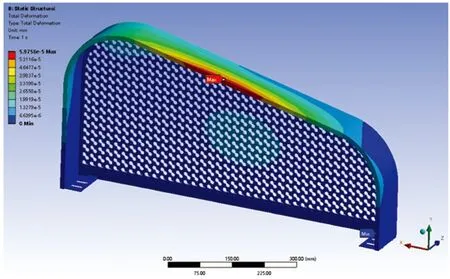
图6 护盖网总位移云图/mm

图7 护盖网等效应力云图/MPa

5 模态分析

将稳态分析的结果作为模态分析的输入条件，进行含预应力的模态分析，计算得到护盖网的前3阶振型，图8～10仅给出护盖网的前3阶振型。由图可见，护盖网的最大振幅均在刚性强度较小的链条网面，角件处焊缝对于振型的影响可以忽略不计。

图8 护盖网第1阶振型/mm

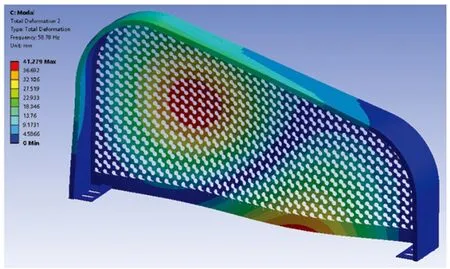
图9 护盖网第2阶振型/mm

图10 护盖网第3阶振型/mm

护盖网模态分析的各阶振型频率如表2所示。活塞式空压机VA-80的额定转速为1100 r/min，缸数为2，则活塞式空压机激振振源的基频1100/60=18.3 Hz，最大激振频率为1100×2/60=36.7 Hz。表3是护盖网前2阶振型频率与激振频率差值对比表，表中数值为护盖网振型频率和活塞式空压机激振频率差值绝对值与活塞式空压机激振频率之比。由表可得，护盖网的前2阶振型频率与激振振源的频率差值范围均大于10%，满足护盖网不发生共振的判定条件，护盖网在活塞式空压机工作时安全稳定。

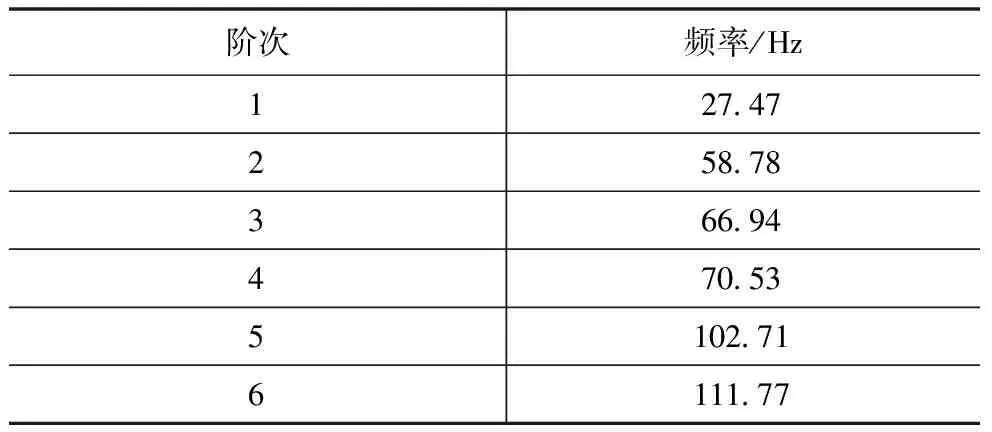
表2 护盖网各阶型频率

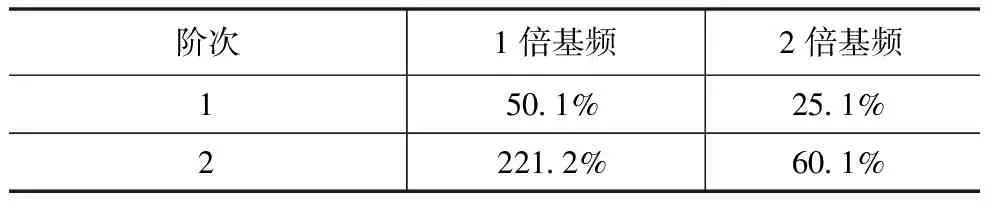
表3 护盖网振型频率与激振频率差值对比表

6 随机振动分析

根据GB/T 21563-2018《轨道交通机车车辆设备冲击和振动试验》，A类车体的安装ASD频谱如图11所示，参数见表4。其中f1和f2的取值如下：

表4 A类车体安装ASD频谱参数表

图11 A类车体安装ASD频谱图

(1)当质量<500 kg时，f1=5 Hz，f2=150 Hz；

(2)当500 kg<质量<1250 kg时，f1=(1250/质量)×2 Hz，f2=(1250/质量)×60 Hz；

(3)当质量>1250 kg时，f1=2 Hz，f2=60 Hz。

由图11、表4可得，活塞式空压机护盖网应在表5的ASD频谱随机振动试验下安全稳定。将下表的各方向的ASD频谱作为输入条件，进行护盖网的随机振动分析。

表5 护盖网ASD频谱

随机振动分析得到护盖网各方向的位移如图12～14所示，各方向的位移云图均是在高斯分布1σ内的位移结果。由图可知，护盖网的在X、Y和Z方向的最大位移分别为0.0065 mm、0.0184 mm和0.1229 mm，最大位移的位置分别位于网罩边框左侧内边缘、网罩边框顶部和链条网底部。其中，护盖网模型的X方向为底部横梁的长度方向，Y方向为竖直方向，Z方向为链条网网面的法向。护盖网在X方向和Y方向的位移都比较小，在Z方向的位移较大，即链条网面的法向振幅较大。

图12 X方向位移云图/mm

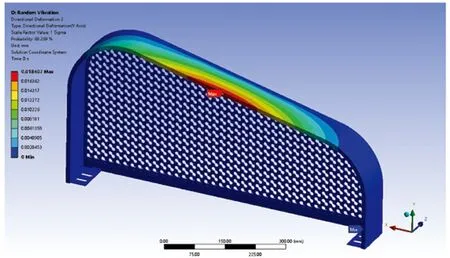
图13 Y方向位移云图/mm

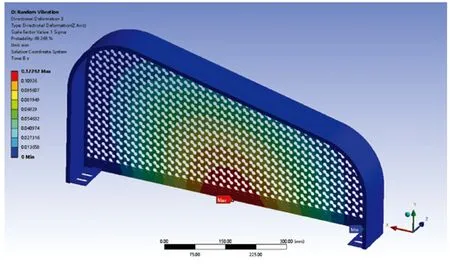
图14 Z方向位移云图/mm

随机振动分析得到护盖网的等效应力如图15。所示，等效应力云图是在高斯分布1σ内的应力结果。由图可知，护盖网的最大等效应力分别为15.14 MPa，最大等效应力的位置在左侧角件的焊缝区域。在随机振动下，相比其它区域，角件和底部横梁焊接区域的截面相对较小，因此最大等效应力会出现在该区域。但是，各方向的最大应力数值都远小于屈服强度，护盖网在随机振动下强度可靠。

图15 等效应力云图/MPa

随机振动分析得到护盖网各方向的速度如图16～18所示，各方向的烈度云图均是在高斯分布1σ内的烈度结果。由图可知，护盖网的在X、Y和Z方向的最大烈度分别为6.17 mm/s、10.78 mm/s和21.99 mm/s，最大烈度的位置分别位于网罩边框左侧内边缘、网罩边框顶部和链条网底部，与最大位移的位置分布大致相同。护盖网在Z方向的烈度较大，即链条网面的法向烈度较大。

图16 X方向振动烈度云图/mm·s-1

图17 Y方向振动烈度云图/mm·s-1

图18 Z方向振动烈度云图/mm·s-1

根据GB/T 7777-2003《容积式压缩机机械振动测量与评价》，往复压缩机振动烈度应满足表6所示标准。活塞式空压机VA-80为非固定式的微型往复式压缩机，最大振动烈度应小于45 mm/s。由随机振动分析得到，护盖网各方向的最大振动烈度分别为6.17 mm/s、10.78 mm/s和21.99 mm/s，均小于标准的45 mm/s，护盖网振动烈度在安全范围内。

表6 往复压缩机振动烈度标准

6 结论

本文针对活塞式空压机VA-80护盖网，利用Workbench建立三维有限元模型，根据实际工艺和安装方式施加边界条件，进行稳态结构分析，计算得到了护盖网的稳态位移和应力。以稳态结构分析结果作为预应力，进行模态分析，得到了护盖网的各阶振型和频率。在模态分析的基础上，按照GB/T 21563-2018《轨道交通机车车辆设备冲击和振动试验》进行随机振动分析，得到随机振动下护盖网各个方向的位移、应力和烈度。由稳态结构分析、模态分析和随机振动分析，本文得到以下结论：

(1)护盖网在稳态情况下，仅受重力及固定约束，位移和应力均处于一个较小值，结构稳定可靠。

(2)前3阶振型护盖网的最大振幅均在刚性强度较小的链条网面，角件处焊缝对于振型的影响可以忽略不计。

(3)护盖网的前2阶振型频率与激振振源的频率差值范围均大于10%，满足护盖网不发生共振的判定条件，护盖网在活塞式空压机工作时安全稳定。

(4)护盖网各方向的最大应力数值都远小于屈服强度，护盖网在随机振动下强度可靠。

(5)护盖网各方向的最大振动烈度分别为6.17 mm/s、10.78 mm/s以及21.99 mm/s，均小于标准的45 mm/s，护盖网振动烈度在安全范围内。

综上所述，活塞式空压机VA-80护盖网稳态工况结构稳定，与激振振源不发生共振，在随机振动下振动烈度在安全范围内，活塞式空压机VA-80护盖网结构安全可靠。