带有混合时滞的中立型随机神经网络的状态估计
彭 杰,张玉武
(1.六安职业技术学院 基础部,安徽 六安 237158;2.武汉大学 数学与统计学院,湖北 武汉 430072)
1982年,Hopfield 教授提出了Hopfield网络模型,阐明了神经网络与动力学之间的关系,开创了神经网络用于联想记忆和优化计算的新途径,引发了人工神经网络的研究热潮。多年来,神经网络被广泛应用于众多领域,如序列识别、联想记忆、信号过程等[1-3]。在具体工程应用中,神经网络通过电子电路构造来完成,一方面,神经元之间的信息传递存在延迟,另一方面,在网络的硬件实现过程中也有开关延迟和通信延迟的存在,这两方面的原因导致了在神经网络中产生了时滞现象。需要注意的是,时滞不只是出现在系统状态(或输出)中,也可以出现在系统状态的导数中,这种时滞被称为中立型时滞,并可在实际应用中找到各种应用案例,如化学反应器、传输线、在超大规模集成电路(VLSI)系统中的部分元等效电路,以及 Lotka-Volterra 系统等。此外,在许多应用中,神经元的状态并不是经常能够在网络输出中完全获取的。因此,神经网络的状态估计在许多应用中变得非常重要。状态估计的主要目标是通过可得的输出测量估计神经元状态,这样的状态估计误差系统的动力学是全局稳定的。关于时滞神经网络的状态估计问题有很多研究结果。例如,杜雨薇等人研究了事件触发机制下混合时滞神经网络的状态估计问题[4];LIANG J等人讨论了一类具有分布时滞的递归神经网络的全局输出收敛性,其中连接权矩阵的对称性和激励函数的有界性是不需要的[5];WANG Z等人通过使用一种有效的LMI方法处理了一类具有离散和分布时滞的神经网络的全局渐近稳定性问题[6];崔颖通过构造具有三重求和项的Lyapunov泛函方法得到了一类离散时间切换神经网络的随机稳定性判据[7];Rakkiyappan R等人设计了基于触发的反馈牵制控制算法[8]。然而,对于既含有离散时滞又含有无穷分布时滞的中立型神经网络的状态估计问题,特别是这些时滞依赖于马尔可夫链变化的研究相对较少。基于此,本文研究了一类具有Markov跳变参数的中立型神经网络的状态估计问题,所考虑的神经网络含有Markov模态依赖的离散时滞和无穷分布时滞。
1 预备知识
1.1 模型描述
设{r(t),t≥0}是概率空间上右连续的Markovian过程,取值于有限空间={1,2,…,n0},其转移率矩阵∏=(πij)(i,j∈S)满足
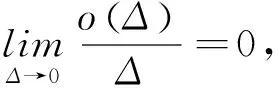
本文考虑由n0个神经元构成的具有Markovian跳参数的中立型神经网络:
(1)
其中x(t)=[x1(t),x2(t),…,xn(t)]T∈Rn是神经网络的状态向量;A(r(t))=diag{a1r(t),a2r(t),…,anr(t)}是air(t)>0的对角矩阵;B(r(t))=(bij(r(t)))n×n,C(r(t))=(cij(r(t)))n×n,D(r(t))=(dij(r(t)))n×n及E(r(t))=(eij(r(t)))n×n表示神经元的连接权矩阵;U(r(t))=[u1(r(t)),u2(r(t)),…,un(r(t))]T是输入向量值函数;F(·)=(f1(·),f2(·),…,fn(·))T,G(·)=(g1(·),g2(·),…,gn(·))T及H(·)=(h1(·),h2(·),…,hn(·))T表示激励函数向量;τ1,r(t),τ2,r(t)表示模式依赖离散时滞,τ3,r(t)表示分布时滞的模式依赖上界。
传统上,我们假设激励函数是连续可微、单调增加且有界的,如sigmoid型函数。然而,在许多电路中,放大器的输入—输出函数既不是单调增加的也不是连续可微的,因此当设计与应用人工神经网络时,非单调函数更适合于描述神经元的激励函数。对于神经元的激励函数,给出下面的假设条件,其中激励函数不再是可微、单调增加及有界的。
假设1 对于i∈{1,2,…,n},在(1)中的神经元激励函数满足
其中,li-,li+,σi-,σi+,υi-,υi+为常数。
注1 假设1中的常数li-,li+,σi-,σi+,υi-,υi+,可以是正数,负数或零,因此,激励函数可以是非单调的,并且比常用的sigmoid函数更一般。注意,为了本文的状态估计,像通常一样,未假设(1)中的激励函数是有界的。
假设2 时滞核φ(·):[0,+∞]→[0,+∞]是连续可积的且满足
(2)
值得注意,无论生物神经网络还是人工神经网络,我们都不能完全获得神经网络的状态,获取的所有信息仅是神经网络的输出。因此,在一些实际应用中,为了实现某些特殊的设计目标,必须由已知的神经网络输出估计神经元的状态,这就需要我们构造估计器,使得状态估计以渐近的方式来逼近神经网络的状态。
设神经网络(1)的输出形式为
y(t)=W(r(t))x(t)+Q(t,x(t))
(3)
其中y(t)=(y1(t),y2(t),…,ym(t))T∈Rm是神经网络的测量输出,W(r(t))∈Rm×n是已知常数矩阵,Q(t,x(t))=(q1(t,x(t)),q2(t,x(t)),…,qm(t,x(t)))T∈Rm是依赖于神经元状态的非线性扰动,并且满足Lipschitz条件:
|Q(t,x)-Q(t,y)|≤|L(x-y)|,
(4)
其中L∈Rn×n是已知常数矩阵。
为了估计(1)的神经元状态,我们构造下面的全阶状态估计器:
(5)
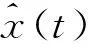
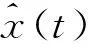
(6)
其中Ak(r(t))∶=-A(r(t))-K(r(t))W(r(t)),为了记号的简单,记
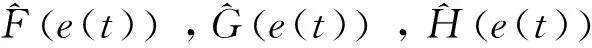
由假设1及(4)得
(7)
设e(t,φ)简记为e(t),表示状态估计误差系统(6)的解,其初始条件为e(s)=φ(s),s∈(-∞,0),其中φ(·)∈C((-∞,0);Rn)。由假设1及条件(4)易知,对于t≥0,系统(1)的解是存在且唯一的。此外状态估计误差系统(6)存在唯一的零平衡点。
1.2 基本定义和引理
为了设计所需要的状态估计器,需要下面的定义。
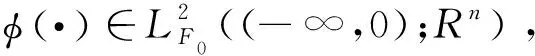
定义2 若状态估计误差系统(6)是全局均方渐近稳定的,则称系统(5)是神经网络(1)的状态估计器。
我们将设计带有Markovian跳参数的中立型神经网络的状态估计器,使得对于每一种模态,系统(6)的动力学是全局均方渐近稳定的。
引理1[9]设X,Y是任意n维实向量且P是n×n阶正定矩阵,则2XTPY≤XTPX+YTPY.
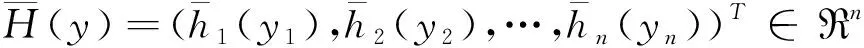
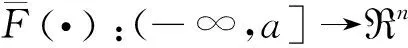
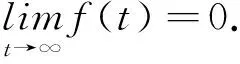
2 主要结果
2.1 状态估计误差系统的全局均方渐近稳定性
为了表达方便,记
现在,我们探讨误差系统的稳定性问题,即得出状态估计误差系统(6)的全局均方渐近稳定的充分条件,进而可根据定义2得到系统(5)是中立型神经网络(1)的状态估计器的充分条件。
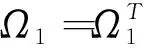
定理1 设已知估计器增益矩阵K(i)(i∈S),在假设1-2条件下,若存在常数ρi>0(i∈S),n×n阶矩阵Pi>0(i∈S),Q>0,R>0,S>0(i∈S)及正定对角矩阵Λi,Θi,Ωi(i∈S),使得下面矩阵不等式对于i=1,2,…n0成立,
(8)
其中
则系统(6)是全局均方渐近稳定的。
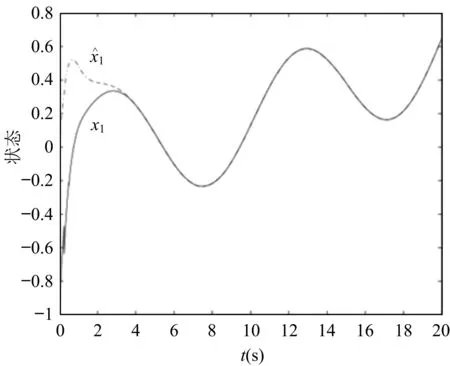
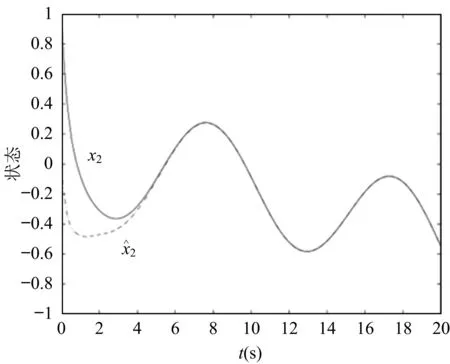
证明定义et(·)为et(s)=e(t+s)(-∞ (9) 其中 设L是沿着系统(6)的随机过程{(et,r(t)):t≥0}的弱无穷小算子,其定义为 于是我们有 (10) 关于LVk(et,t,i)(k=1,2,…,6)的计算如下: (11) (12) 类似于(12)式得 (13) 易见 (14) 此外,我们可推出 (15) 最后,我们有 (16) 将(11)—(16)代入(10)式中,可以得到 (17) 由假设1及引理2,可推出 (18) (19) (20) 此外,由引理3,易知 (21) 因此,由(18)—(21)式,可以得到 其中 设λ0=max{λ1|i∈Smax,显然,λ0<0,于是LV(et,t,i)≤λ0|e(t)|2.因此, 现在需要研究状态估计器的设计问题,即计算出估计器的增益矩阵K(i)(i∈S),使得定理1的一组矩阵不等式(8)成立。显然,由于它们是非线性的并且其中含有许多参数,很难解矩阵不等式(8)。解决这种问题的一种有意义的方法是将非线性耦合矩阵不等式转化为线性矩阵不等式(LMIs),与此同时,可以计算出估计器的增益矩阵。 下面的定理说明,若一组LMIs是可行的,则可以设计出所需要的估计器的增益矩阵。 定理2 在假设1-2条件下,若存在常数ρi>0(1≤i≤n0),n×n阶矩阵Pi>0(1≤i≤n0),Q>0,R>0,S>0,n×n阶对角矩阵Λi>0,Σi>0,Ωi>0(1≤i≤n0)和n×m阶矩阵Mi,Ni(1≤i≤n0)使得下面LMIs是可行的 其中 证明设Mi=PiK(i),Ni=QK(i),1≤i≤n0,则由引理4可知Ψ2(i)<0等价于Ψ1(i)<0,从而由定理1可以得到当K(i)=Pi-1Mi时误差状态系统(6)是全局均方渐近稳定的。 下面针对所讨论的中立型神经网络,给出二维中立型神经网络实例来说明提出的状态估计器设计方法的有效性。 例 考虑具有Markov跳参数的二维中立型神经网络,其中系统的参数取值如下: 取激励函数为 以及时滞核函数为φ(s)=e-3s.易验证 根据上面的参数,并应用Matlab线性矩阵不等式工具箱求解LMIs可得下面的可行解: 根据定理1、2可知,此系统是渐进稳定的。状态估计器增益矩阵为 图1 真实状态x1与估计状态 图2 真实状态x2与估计状态 对于含有Markov模态依赖的离散时滞和无穷分布时滞的中立型神经网络,通过构造新的Lyapunov-Krasovskii泛函以及应用一些新的随机分析技巧,可以推导出状态估计误差系统全局渐近稳定的充分条件,从而保证了所考虑神经网络的全阶状态估计器的存在。在这些充分条件的基础上,通过将非线性耦合的矩阵不等式转化为线性矩阵不等式,借助线性矩阵不等式(LIMs)的可行性解决神经元的状态估计问题,并运用Matlab LMI Toolbox进行求解,从数值例子可以看出所设计的状态估计器的有效性和可行性。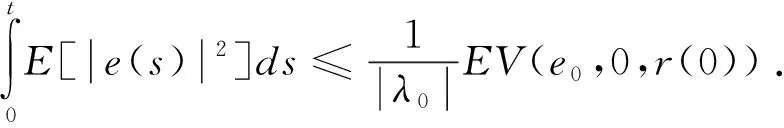
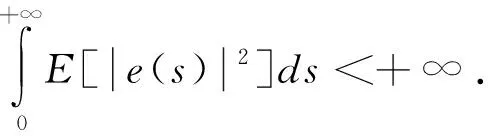
2.2 状态估计器的设计
3 数值举例
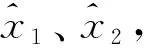
4 结语

