研究关联方法,“圆”来如此美妙
第二章 对称图形——圆
领衔人:浦叙德(正高级教师、江苏省特级教师)
组稿团队:江苏省无锡市初中数学浦叙德名师工作室
本章是初中平面几何中非常特殊的一章,在此之前和之后学习的平面图形都是直线型,唯独这章研究的是曲线型。因为圆是现实世界中常见的基本图形,应用非常广泛,所以我们非常有必要详细深入地研究它。如果我们梳理本章知识,研究这些知识之间的关联,你就会觉得,“圆”来如此美妙。
一、知识之间的关联结构
从数学研究的基本套路出发,我们要研究一个对象的定义、性质、判定,或两个对象之间的关系,包括位置关系和数量关系,然后利用研究结果解决数学问题或实际问题。
1.知识要点
本章内容一共有8个小节,可以分成两大板块。一块是研究一个对象,即圆的定义,利用圆的轴对称性证明了垂径定理,利用圆的旋转不变性说明了圆心角、弧、弦之间的关系,利用同弧作为中介,对圆周角、圆心角进行分类讨论,通过一般到特殊的转化,证明了圆周角定理,最后利用小学里所学的圆的周长、圆的面积知识分别推导出弧长公式、扇形的面积公式;另一块是研究两个对象之间的关系,即点与圆的位置关系,直线与圆的位置关系,三角形、四边形、正多边形与圆的位置关系,特别研究了直线与圆相切的特殊情形,得出了切线长定理。点与圆、直线与圆的位置关系,反映了形与数之间的内在联系,即由图形的位置关系决定数量关系,由数量关系判定图形的位置关系。
2.关联结构
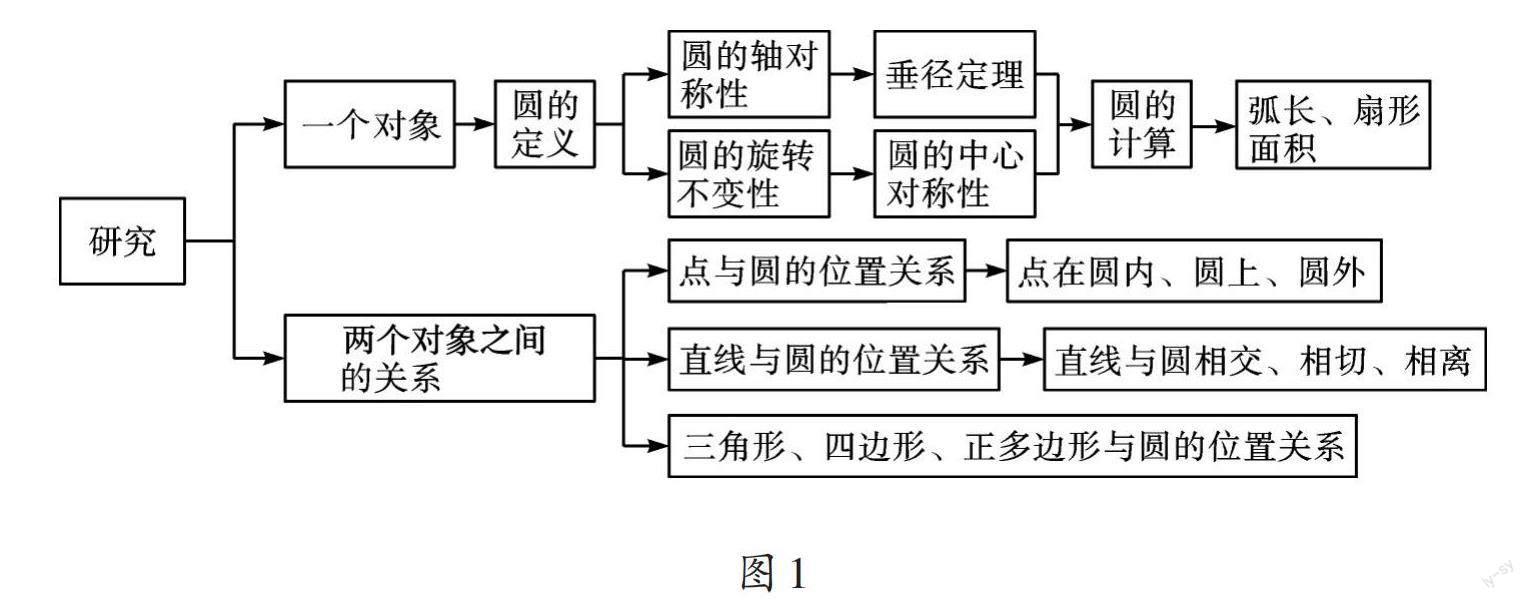
数学知识之间存在着一定的逻辑关系,这种关系体现知识从哪里来、怎样形成、到哪里去,只有明确了知识的来龙去脉,方能从整体上真正理解数学知识。通过对本章知识之间的逻辑关系进行归纳,我们可以得到如下的知识结构图(如图1)。
二、研究知识的主要方法
本章内容的研究主要用到三种重要的思想方法:特殊与一般,形数转换,分类讨论。其中,分类讨论主要是由形的位置不确定而引起,如教材中证明圆周角定理等。因此,同学们在学习知识的同时,一定要深刻领会这些数学思想方法在其中的重要作用。下面,就本章中涉及的“特殊与一般”与“形数转换”进行具体说明。
1.特殊与一般
如果把曲线型圆与前面的直线型图形联系起来看,本章的研究内容始终围绕着“直线型与圆之间的关系”展开,处处存在特殊与一般的研究方法。研究位置关系的具体知识有:(1)点与圆的位置关系,分为“点在圆内、点在圆上、点在圆外”三种,其中重点研究“点在圆上”;(2)直线与圆的位置关系,分为“直线与圆相交、直线与圆相切、直线与圆相离”三种,其中重点研究“直线与圆相切”;(3)角与圆的位置关系,按角的顶点位置分为“圆内角、圆上角、圆外角”三种,其中重点研究“圆心角、圆周角”两种;(4)三角形与圆的位置关系,重点研究“圆的内接三角形、三角形的内切圆”;(5)四边形与圆的位置关系,重点研究“圆的内接四边形、四边形的内切圆”;(6)正多边形与圆的位置关系,重点研究“圆的内接正多边形、正多边形的内切圆”。研究数量关系的具体知识有:(1)圆周长与弧长;(2)圆面积与扇形面积。当然,在研究具体某个知识时,也多次用到特殊与一般的关系,如“弦与直徑”“弧与半圆”“垂径定理”等。可见,特殊与一般,既是我们认识事物的一般规律,也是研究数学非常重要的思想方法。
2.形数转换
平面几何主要研究一个图形的定义、性质、判定和两个图形的位置关系、数量关系,圆的研究也不例外。因此,本章的研究始终围绕着“数与形”的转换展开。
例如,要研究点与圆的关系,我们可以直接从形的角度“点在圆内、点在圆上、点在圆外”入手直观判断。而“形缺数时难入微”,我们可以通过点心距d与半径r之间的数量关系加以判断,即“当d<r时,点在圆内;当d=r时,点在圆上;当d>r时,点在圆外”。同样,我们要研究直线与圆的关系,可以直接从形的角度“2个交点、1个交点、0个交点”直观判断,也可以通过圆心距d与半径r之间的数量关系加以判断,即“当d<r时,直线与圆相交;当d=r时,直线与圆相切;当d>r时,直线与圆相离”。如果要对教材知识进一步推广,如研究圆与圆的关系,同样可以通过“形数转换”的思路,从位置关系的形与数量关系的数两个视角来展开。
通过上面的介绍,我们不但明确了圆这一章知识的逻辑关系及其关联结构,而且知道了研究本章内容时用到的重要思想方法,这样就形成了对圆的整体性的本质认识。对数学知识的学习,我们不仅要明白研究内容,更要明白研究这些内容的主要方法,这将有助于我们对数学学科的进一步学习和迁移创新。
(作者单位:江苏省无锡市新吴区教师发展中心)

