三角函数中求解ω 常见问题及解题策略
2023-11-11 06:10彭科
高中数理化 2023年19期
彭 科
(广东省东莞市东莞中学松山湖学校)
作为高考中的必考问题,每年试卷中都会出现一些与三角函数相关的题目.在三角函数y=Asin(ωx+φ)(A>0,ω>0)中,ω的变化会引起函数图像、单调性、周期等一系列性质的变化,因此求ω的取值成为考试中常见的问题.为帮助学生全面认识相关问题,本文总结常见的题型及解题策略.
1 单调性问题
三角函数y=Asin(ωx+φ)(A>0,ω>0)可以视为由函数y=Asinu与u=ωx+φ复合而成.因为函数u=ωx+φ(ω>0)单 调 递 增,所 以 欲 求y=Asin(ωx+φ)(A>0,ω>0)的单调递增区间,只需求y=Asinu(A>0)的单调递增区间.由


2 零点问题
零点问题往往需要学生结合函数的图像进行解答.在实际解题中,学生应将零点问题与函数同x轴的交点坐标进行联系,然后进行计算求解.需要注意的是,学生应注意图像平衡位置的变化,当函数图像的对称点不在x轴上时,相邻两零点的距离便不为.

3 最值问题
三角函数的最大值或最小值往往出现在其对称轴上.因此,当题目中出现某一值恒大于(或小于)其他值时,则可确定此点在对称轴上.

综上,选C.
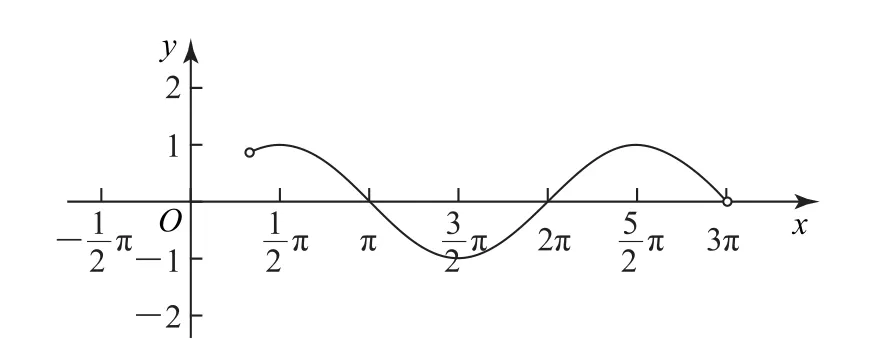
图1
4 对称性问题


5 周期性问题

综上,因为三角函数中ω的取值会直接影响函数的诸多性质,所以将诸多性质与ω进行综合考查的问题频繁出现在高考试卷中.本文详细地总结了5种已知三角函数性质求ω取值问题的解题策略,以期提升学生的解题效率.函数y=Asin(ωx+φ)的图像源于y=sinx,y=Acos(ωx+φ)的图像源于y=cosx,因此,无论函数怎样变化,只要学生能够熟练掌握相关性质,就能顺利解答与ω有关的取值问题.
(完)
猜你喜欢
数理化解题研究(2020年25期)2020-10-11
数理化解题研究(2020年13期)2020-05-07
郑州大学学报(理学版)(2020年1期)2020-02-08
数学物理学报(2019年5期)2019-11-29
中学生数理化(高中版.高考数学)(2019年9期)2019-11-27
中学生数理化·七年级数学人教版(2017年10期)2017-04-23
福建中学数学(2016年2期)2016-10-19
数学大王·低年级(2016年10期)2016-09-10
物理与工程(2010年5期)2010-03-25

