从通性通法的角度谈均值不等式的应用

朴今子 付 禹

(吉林省长春市第十一高中)

在运用均值不等式解决有关问题时,经常会强调“一正、二定、三相等”.可从通性通法的角度去理解这句话的含义:在运用均值不等式解决有关问题时,在注意变量为正数的前提下,可以考虑“构造法”,但“如何构造”是关键,下面从两个方面进行说明.

1 侧重定值构造

1.1 侧重乘积为定值构造

例1 已知x＞1,则函数的最小值为_________.

分析 因为函数表达式中的分式中有分母(x－1),所以在函数表达式中只需构造(x－1),进而可以按以下方式求最小值.

解 因为x＞1,所以x－1＞0,则

答案－1.

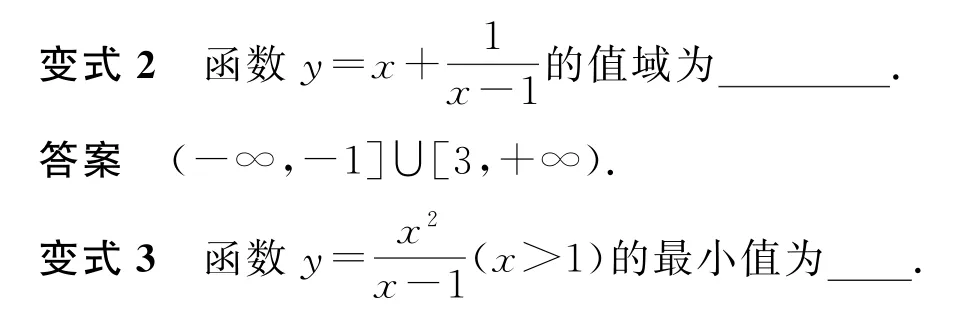
答案 4.

例1及三个变式的表达式比较明显地提供了相同的信息,即构造乘积为定值,变式3构造的难度大一点.若函数表达式的结构中不易发现这种特殊结构(条件隐蔽),那么如何构造呢? 下面一起来看看下面的例题.

分析 观察现有函数表达式的结构,很难构造乘积为定值的结构,而根据分式的性质将函数表达式化为后就会发现两个分式的分母之和是常数,进而通过变形可以构造互为倒数的两个分式

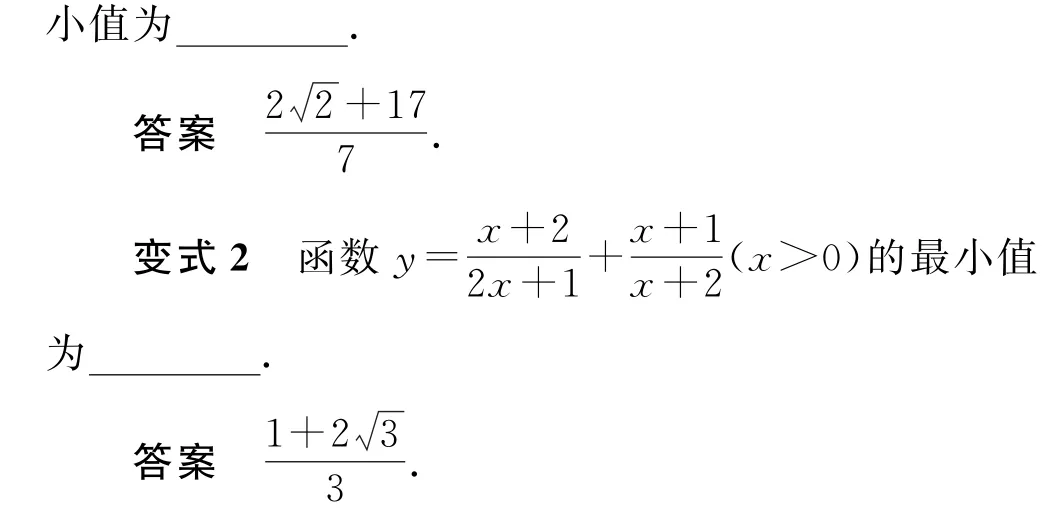
本例及其变式都是利用均值不等式求解的有关问题中比较难的问题,难点在于如何构造,而突破这个难点的关键在于注意观察表达式的结构中隐含的条件.

例3 已知a＞0,b＞0,c＞0,求证:

分析 观察不等式左边结构,不难发现每项分式的分子、分母之和都是a＋b＋c,而三项分式的分母之和是a＋b＋c的2倍,由此可以考虑先用均值不等式构造两个不等式.

解 由均值不等式得

此题有多种证法,从通性通法的角度来看,通过构造乘积为定值的方法去寻找思路显得比较自然.此例还可以进行如下推广.

变式 已知xi＞0(i＝1,2,…,n,n∈N),且n≥2,求证

提示 由均值不等式得

1.2 侧重和为定值构造

例4 函数y＝x4(1－x2)(0＜x＜1)的最大值为_________.

“构造和为定值”相对于“构造积为定值”要容易很多,主要原因是需要“构造和为定值”的表达式比较单一(乘积结构).本题的变式难度略大,原因是构造时要想到隐含条件“sin2x＋cos2x＝1”.

2 侧重取等号角度构造

例5 已知a＞0,b＞0,且满足a＋b＝1,求证:

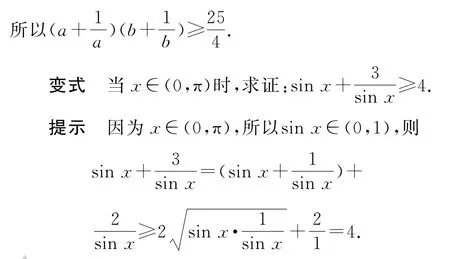
在运用均值不等式的过程中,若已知条件和结论中的代数结构是“对称轮换式”(根据加法和乘法的交换律及结合律,将式子f(x1,x2,…,xn)(n∈N∗)中任意元xi与xj(i≠j)交换位置,表达式保持不变),则取等号的条件就是各元相等.

本文从通性通法的角度介绍了均值不等式应用中的两种构造法,在不等式的证明中通常需要通过放缩转化后再运用上述方法求解.

(完)