利用不等式求解最值问题的解法探究

田素伟

(上海市泥城中学)

求代数式的最值问题是高中数学中一类非常重要的问题,这类问题通常以不等式、三角函数、数列、向量为载体,考查不等式性质的应用,很多问题还涉及均值不等式.如果选择恰当的方法,把比较复杂的问题转化为我们熟悉的较为简单的问题,会起到事半功倍的效果,下面通过具体例题说明利用不等式求解最值问题的解法探究.

1 均值不等式的说明及举例

均值不等式(基本不等式):两个正数的算术平均数大于或等于它们的几何平均数,即对于任意的正数a,b,有,当且仅当a＝b时,等号成立.

应用均值不等式求解最值的条件有三个.

1)a,b是正数;

2)a＋b或ab是定值;

3)存在满足条件的a,b使a＝b成立.

这三个条件同时满足才能使用均值不等式,三个条件缺一不可,即“一正、二定、三相等”.

例1 已知a＞0,b＞0满足a＋b＝1,则的最小值是_________.

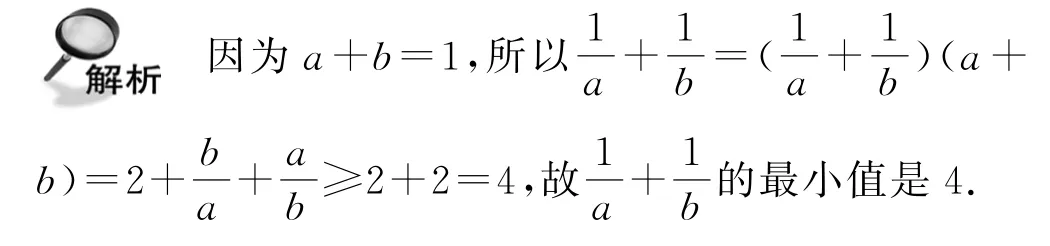
这是一道非常熟悉的题目,利用乘1法即可求解,但是对于比较复杂的题目,如何以例1为模型,通过变换使之转化为形如例1这样熟悉的题目呢? 这是我们需要探究的问题.

2 已知条件是含整式的等式,求分式二元变量的最值问题

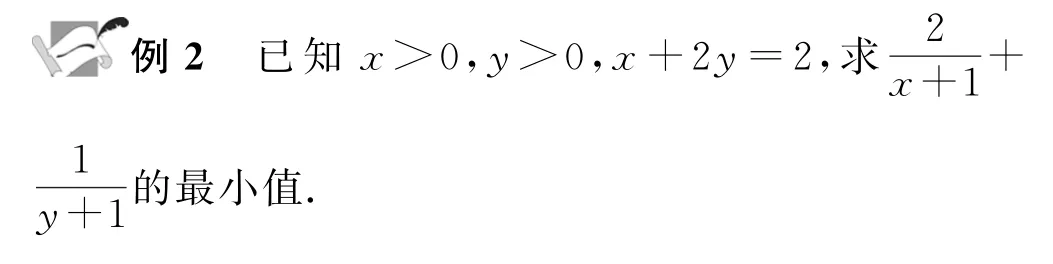
方法1 已知x＞0,y＞0,设m＝x＋1,n＝2y＋2,则

即m＋n＝5,所以

故原题可化为:已知m＞1,n＞2满足m＋n＝5,求的最小值.又

经过换元把原题转化为:已知正数m＞1,n＞2,m＋n＝5,求的最小值这样比较熟悉的题目了,使题目简化,使解题过程简单明了.需要注意观察已知条件等式和所求的代数式中变量的系数再进行换元.

方法2 由x＋2y＝2,可知

方法2 是利用权方和不等式求解,简单明了,填空题或选择题可以直接应用权方和不等式求解,权方和不等式作为柯西不等式的分式形式,在求二元变量的最值时有非常广泛的应用.权方和不等式:设a＞0,b＞0,x＞0,y＞0,则,当且仅当时,等号成立.利用权方和不等式求解最值的一般步骤如下.

第一步:先看分式的分母之和是不是定值,分子之和是不是定值,若不是定值,能否通过变形后使之变成定值;

第二步:使用权方和不等式变形,使分子的指数比分母大1即可;

第三步:检验等号成立的条件.

3 已知条件是含分式的等式,求整式二元变量的最值问题

方法2利用权方和不等式求解,简单明了,能起到事半功倍的效果.下面的各个题目均可利用权方和不等式求解.

4 均值不等式在求函数最小值时的应用

本题变形后用换元法把比较复杂的不等式转化为熟悉的形式,再利用均值不等式求解,简洁明了.

5 与三角函数有关的问题求最值

6 直接利用均值不等式求最值

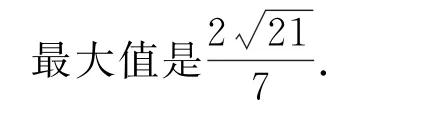
通过观察已知条件,发现9x2＋y2＋xy＝1中含有9x2＋y2,且结论中含有代数式3x＋y,因此也可以利用完全平方公式求解,即9x2＋y2＋6xy＝(3x＋y)2,再利用均值不等式求解.

7 构造向量求最值

链接练习

链接练习参考答案

(完)