混合悬浮电磁铁结构优化设计

卢相宇，马卫华，张 敏，罗世辉，曹 毅

（西南交通大学 牵引动力国家重点实验室，成都 610031）

目前磁浮列车悬浮系统根据悬浮方式主要可以分为：电动悬浮、电磁悬浮以及混合悬浮［1］。不同的悬浮模式具有不同的优缺点，其中电动悬浮不消耗能量但是稳定性较差。而电磁悬浮方面，大量试验和工程实践已经证明结构简单的电磁悬浮是可行的，但这种只依靠电磁感应产生悬浮力的悬浮模式在稳定悬浮时由于电磁铁流过的电流较大，功耗相对增大使得电磁铁线圈发热较为严重［2-4］。

混合悬浮电磁铁工作在额定悬浮点的时候，大部分悬浮力由混合悬浮电磁铁中的永磁体提供，因此电磁铁线圈部分只需要提供一小部分的电磁力起调节作用［5］，用来克服外界的干扰，这使得整体的功耗和发热降低，同时也保障了足够的悬浮力。因此国内外许多学者对混合悬浮模式进行了相关研究。张颖、李云钢等人根据力学模型提出了增大混合磁铁磁轭高度以提高承载力的方法，并且通过理论分析及仿真得到结论：适当增大永磁截面积能提高磁铁可控性［6］。金森、刘国清等人研究了一种基于不等宽结构的混合悬浮装置，通过仿真和试验验证，证明在改进的不等宽混合悬浮装置中，无论气隙间距大小如何，可实现列车悬浮的“零功率”控制［7］。陈慧星设计了一种混合磁铁，并导出了在最优间隙反馈系数下混合磁铁结构的最优悬浮刚度，适当增加永磁体的截面积能提高混合磁铁的承载能力、可控性及悬浮刚度［8］。陈贵荣提出一种新型的电磁铁结构并建立数学模型，证明永磁体提供的悬浮力可满足列车额定载荷的零功率控制要求，控制系统最大反向电流不会引起永磁体失磁［9］。

文中针对传统的混合悬浮电磁铁结构，在原有的基础上深入分析混合悬浮模式下的电磁场，研究其漏磁的原因并针对性地提出减小漏磁的改进措施。基于实例给出永磁体参数的设计方法，提高永磁体的利用率，并通过试验对仿真结果进行验证。

1 混合悬浮电磁铁结构及数学模型

混合悬浮电磁铁结构本质上是通过在纯电磁铁中引入永磁体，由永磁体来提供部分悬浮力。对比不同的永磁体引入方式，文中着重分析混合悬浮电磁铁的结构如图1 所示，永磁体位于铁芯的一侧，其优点是永磁体的厚度及高度易于调整，且受温升影响较低。

图1 混合悬浮电磁铁结构

运用等效磁路法对图1 的混合电磁铁结构进行分析，首先做出如下假设：

（1）忽略铁磁材料的磁饱和效应。

（2）忽略铁芯、极板及轨道的磁阻。

（3）不考虑线圈和永磁体漏磁所带来的影响。

为建立悬浮力的数学模型，首先定义基本参数，气隙长度为δ、气隙磁路面积为S、永磁体的矫顽力为Hc、相对磁导率为μm、永磁体厚度为d、永磁体高度为h、永磁体长度为l、永磁体在磁路方向上的面积为A、线圈匝数为N、线圈电流为I、真空的磁导率为μ0。根据等效磁路法建立电磁铁回路的等效磁路模型如图2 所示，其中永磁体与电磁线圈为串联关系。

图2 电磁铁等效磁路模型

在图2 中，电磁铁的磁动势可表示为式（1）：

式中：Ui为电磁线图的磁动势；Up为永磁体的磁动势。

永磁体在磁路方向上的面积为式（2）：

永磁体的磁阻表示为式（3）：

气隙磁阻表示为式（4）：

电磁铁回路的气隙磁通表示为式（5）：

混合电磁铁的悬浮力可表示为式（6）：

综合式（1）~式（5）可以得到悬浮力的表达式为式（7）：

2 混合悬浮电磁铁结构优化

在ANSYS 中进行仿真分析，其基本参数见表1。

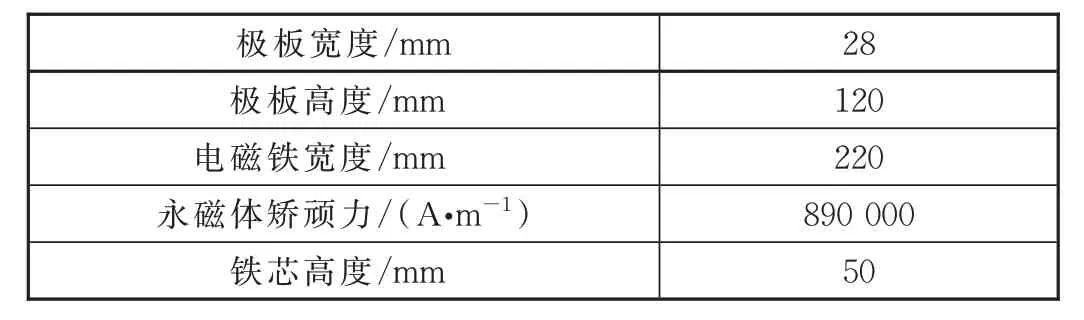
表1 电磁铁基本参数

通过二维仿真，得到其磁力线分布如图3 所示。从图中可以看出永磁体存在漏磁，且主要集中在永磁体高出铁芯的部分。在额定间隙8 mm时，假定永磁体厚度为25 mm，电流为0，悬浮力与永磁体高度的关系如图4 所示。在考虑漏磁的二维仿真中悬浮力与永磁体高度近似成正比关系，而在不考虑漏磁的式（7）中悬浮力与永磁体高度的平方近似成正比关系，也印证出永磁体存在较大漏磁。同时可以看出永磁体高度越高其提供的悬浮力越大，达到相同悬浮力所需电流越小，越节能。所以在不超过极板高度情况下，永磁体高度越高越有利。出于对永磁体的保护，永磁体高度略小于极板高度，可取为115 mm。

图3 磁力线分布图

图4 悬浮力与永磁体高度的关系

为减小漏磁，提高永磁体的磁能利用率，文中提出一种混合悬浮电磁铁改进结构，在永磁体的一侧增加1 块钢板，部分漏磁的磁力线经过钢板进入铁芯，从而减小永磁体的漏磁，具体结构如图5所示。

图5 混合悬浮电磁铁改进结构

为得到合理的钢板厚度，采用二维有限元仿真分析不同永磁体厚度在零电流条件下，悬浮力与钢板厚度的关系，如图6 所示。

图6 钢板厚度与悬浮力关系

从图6 中可以看出，在一定范围内，悬浮力随钢板厚度的增加而增加，钢板厚度超过一个定值后，悬浮力增加趋势变缓，由此确定钢板厚度的合理值，此时，电磁铁悬浮力提高约15%。钢板厚度的选取与永磁厚度有关，永磁体厚度越大，钢板厚度选取值越大，具体值见表2。

表2 不同永磁体厚度对应钢板厚度值

3 混合悬浮方案设计

混合悬浮电磁铁主要由内外极板、永磁体、铁芯及电磁线圈组成，1 块电磁铁包含4 块永磁体和4 个线包，结构如图7 所示。以新型磁浮列车电磁铁为设计目标，空载时电磁铁需提供悬浮力为27 kN，满载时提供悬浮力为39 kN［10］。额定悬浮间隙为8 mm，起浮间隙为16 mm，防吸死间隙为3 mm。为更好的模拟实际情况，采用三维有限元软件进行仿真分析，建立的有限元模型如图8所示。

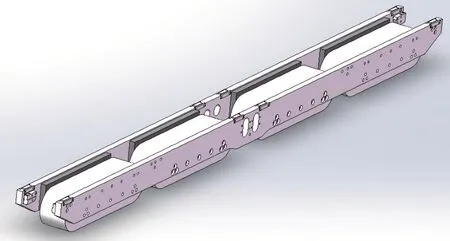
图7 混合悬浮电磁铁三维结构

图8 ANSYS 有限元模型

混合悬浮电磁铁设计关键在于永磁体参数的选取：悬浮力大小与永磁体长度成正比，所以在不发生干涉的情况下，永磁体长度取最大长度，一块永磁体长460 mm。永磁体厚度影响系统可控性、各工况电流大小及钢板厚度的选取，还会影响线圈的宽度。

线圈宽度的考虑：线圈为320 匝，为2 个子线圈串联在一起，材料为铝，一匝线圈的厚度为0.3 mm。为运行安全，线圈需能承受80 A 电流，对应线圈所需宽度为50 mm。线圈与铁芯两端需有1 mm 间隙防止挤压线圈，2 组串联线圈之间的间隙为4 mm，环氧树脂厚5 mm，线圈与环氧树脂之间间距2 mm。永磁体与钢板的厚度值之和不应超过220-50×2-28×2-5×2-2×4-4-2=40（mm）。

可控性考虑：纯电磁铁系统和混合电磁铁系统都是可控的，为对可控性进行定量分析，分别定义纯电磁铁系统和混合电磁铁系统的可控性能函数为式（8）~式（9）［11］：

式中：δ0为额定悬浮间隙；(NI)0为纯电磁铁额定线圈安匝数。可控性能函数值越小，可控性越好，从式中可以看出混合电磁铁系统可控性低于纯电磁铁系统。定义额定间隙下混合电磁铁系统的可控性为纯电磁铁系统的λ倍，其表达式为式（10）：

从式（10）可看出永磁体越厚，λ值越小，控制难度越高，λ取值应在0.7 以上，所以将0.7 代入式（10）可得到永磁体厚度的取值应在28 mm 以下。

各工况电流考虑：在额定间隙悬浮、起浮及吸死3 个悬浮工况下，不同永磁体厚度所对应的钢板厚度为合理厚度，悬浮力与电流关系如图9~图11所示。

图10 间隙16 mm 时悬浮力与电流关系

图11 间隙3 mm 时悬浮力与反向电流关系

电磁铁在额定悬浮间隙及起浮间隙下均需能承受满载时的质量，电磁铁在空载时最容易发生吸死，需通反向电流使悬浮力小于车重，不同永磁体厚度对应不同工况所需电流见表3。额定间隙所需电流为I1，起浮间隙所需最小电流为I2，吸死间隙所需最小反向电流为I3。

表3 不同永磁体厚度对应不同工况所需电流

根据各工况所需电流的大小，并考虑可控性和线圈宽度的要求，永磁体厚度选取25 mm，钢板厚度为13 mm。此时在额定悬浮间隙满载时由永磁体提供的悬浮力占比为62%，空载时占比86%。

4 试验验证

测试悬浮力试验台如图12 所示，测试悬浮力时，F 轨通过防吸死滑块与电磁铁吸合在一起，通过不同高度的滑块来模拟不同的悬浮间隙。F 轨固定在提升平台上，电机驱动平台向上移动，此时的拉脱力即悬浮力由拉力传感器测量。

图12 电磁力试验台

试验时采用1 个线包，1 块电磁铁由4 个线包组成。将试验所得到的悬浮力乘4 视为1 块电磁铁的悬浮力。为验证第3 节所设计混合悬浮电磁铁的悬浮力仿真结果，将间隙3、8、16 mm 时的悬浮力试验结果与仿真结果进行对比，如图13所示。

图13 不同间隙下仿真与试验结果对比

因为仿真是理想化的条件，未考虑温度、摩擦等因素的影响，所以与试验结果有一定误差。从图13 可以看出仿真与试验结果误差并不大，在可以接受的范围之内，证明仿真结果是可信的。

5 结 论

文中提出了一种混合悬浮电磁铁改进方案，利用等效磁路法推导电磁关系，通过ANSYS 对电磁铁优化方案进行仿真分析，并利用试验和仿真结果进行对比，得到如下结论：

（1）和传统方案相比，改进后的方案能降低电磁铁漏磁现象，提高悬浮能力。

（2）钢板厚度的选取随永磁体厚度变化而变化，永磁体厚度越大，对应钢板的厚度越大。

（3）根据实际车型对电磁铁悬浮能力的要求，对混合悬浮电磁铁相关参数进行设计，得到了满足各工况悬浮力要求的电磁铁方案。

（4）通过台架试验证明仿真结果存在一定误差，但整体与试验结果较为接近。