基于拓扑优化设计的动力集中动车组车体变压器梁优化与减重

王肇凯，刘云鹏，王艺飞，李加瑞，张 昭

（1 中车大连机车车辆有限公司，辽宁大连 116022；2 大连理工大学 工业装备结构分析优化与CAE 软件全国重点实验室，辽宁大连 116024）

机车梁是承载的主要结构，其中中梁、侧梁、牵引梁、变压器梁等梁结构尤为重要。在动力集中动车组车体结构设计中，变压器梁承受关键载荷，其设计对整车运行安全性极为重要。

针对车体结构的优化设计可以实现对车身质量控制和各型车体部件质量分配，对实现轴重的精确控制有明显的实用价值。结构优化通常分为3 种，分别针对几何形状、拓扑形貌和尺寸进行优化，其中形状优化和拓扑优化可以帮助设计人员确定几何结构拓扑形貌，尺寸优化可以帮助确定最终的设计尺寸。文献［1］采用拓扑优化确定了司机室加强肋的布局，并进一步设计了车体司机室的加强肋结构。文献［2］针对端墙结构的动态碰撞，进行了拓扑优化设计和进一步的板厚尺寸优化设计，通过优化设计，在满足碰撞安全性的前提下，实现了车体结构在降低正面碰撞力的同时吸能最大化。文献［3］针对动车机箱结构进行了拓扑优化设计，得出蒙皮加强肋的最佳布局型式，其一阶模态频率提高了56.18%。文献［4］针对动车组转向架转臂进行了拓扑优化设计，在最大应力降低的同时，结构质量下降了8.43%。文献［5］基于拓扑优化的设计思想，以动车组行李架支座刚度最大化为设计目标，考虑材料体积约束，对结构材料布局进行优化设计。文献［6］针对机车牵引装置三角架进行了拓扑优化设计，最大应力和最大位移较优化前都明显降低的同时，重量降低了6.8%。文献［7］基于渐进结构优化法（ESO），通过APDL 语言编制拓扑优化程序，对某高速动力车辆转向架构架内部筋板位置进行了拓扑优化设计，尽管应力水平有所上升，但是应力分布更为均匀，结构减重了约10%。以上工作表明，针对车体的拓扑优化设计逐渐成为车体设计的重要辅助手段，对车体结构和车体零部件结构的质量控制具有重要意义。

Bendsøe 和Kikuchi［8］基 于 均 匀 化 的 拓 扑 优 化 方法为拓扑优化的发展奠定了基础，之后发展出多种方法，包括密度法、水平集方法、渐进方法、相场法等［9］。通过拓扑优化方法，可以实现材料在承载下的最优材料布局，但是如何实现材料布局和具体结构尺寸的结合始终是产品拓扑优化设计所需要面临的主要问题。因此，基于传统的拓扑优化设计方法，发展出了多种新方法，以实现拓扑优化和结构设计的直接关联，形成了一系列拓扑优化方法：移动可变形组元方法［10-11］、面向确定工业领域的拓扑设计［12-14］、特征驱动方法［15］、面向具有不确定性特征参数的拓扑计算方法［16-17］等。其中，移动可变形组元方法使用可移动可变形的组件表示拓扑优化区域，具有计算变量少、拓扑优化效率高、边界清晰、易于执行、得到的最优结果能够直接用于几何建模等优点，其执行程序已经开源，见文献［10］。

从上述进展可以看到，如何实现拓扑优化方法和直接结构设计的结合是拓扑优化设计工程化应用的关键。因此，文中提出了一种拓扑优化+尺寸优化的一体化方法，对某型动力集中动车组车体牵引梁结构进行参数化设计，确定结构的最后尺寸和结构布局，在满足TB/T 3548—2019《机车车辆强度设计及试验鉴定规范 总则》和BS EN 12663-1：2010《铁路应用—铁路车辆车体的结构要求》等相关标准的前提下，实现最大程度的结构减重。

1 结构优化模型

以某型动力集中动车组车体为例，如图1 所示，车体大部分组件采用Shell 单元进行网格划分，并对其赋予不同厚度进行模拟，直角支撑位置、驾车点位置实体采用三维实体单元进行网格划分和数值模拟。综合车体结构尺寸，Shell 单元的参考尺寸确定为0.03 m，最小Jacobian 为0.3，共包含403 027 个节点和417 976 个单元，属于大规模计算问题。通过附加质量的方法保证有限元车体质量与实际车体质量保持一致。

图1 动力集中车车体有限元模型

变压器梁在牵引工况下承载最大，选择牵引工况进行拓扑优化设计。先进行拓扑优化的有限元计算，再根据解读后的优化结果重构变压器梁模型，代替原模型的变压器梁结构。将变压器梁设计域确定为3 069×344×419 mm 的设计空间，在此空间内进行优化设计，优化列式为式（1）［18］：

式 中：Cω为 总 的 加 权 应 变 能；fi为 第i个 工 况 的 载荷；Ci为第i个工况的柔度目标函数；ωi为各个工况的柔度函数的权重，其取值在0~1 之间；为位移矩阵的转置矩阵；mi为第i个单元的质量；M为优化区域质量；d为单元密度。变压器梁结构优化如图2 所示。

图2 变压器梁结构优化示意图

根据拓扑优化后得到的变压器梁构型在有限元模型中进行重构，采用最优尺寸设计的变压器梁代入整车计算模型中进行静态强度校核，以满足TB/T 3548—2019、TB/T 2541—2010、EN 12663-1-2010 相关标准的要求［19］。几何尺寸优化的优化列式为式（2）：

式中：M为目标质量，目标函数为目标质量最小；σs为目标材料的屈服强度；t1、t2、t3、t4、t5等设计参数为厚度，在优化设计中，其具体数值以不超过原始设计为准。变压器梁各板厚设计如图3 所示。

图3 变压器梁几何尺寸优化的各设计参数

2 结果与讨论

优化结果如图4 所示，可以看出优化后的变压器梁大体形状与原有设计基本相似，但是侧板形状与原结构形状有所不同。基于拓扑优化的计算结果，对变压器梁结构进行几何重构，并划分有限元网格，如图5 所示。

图4 变压器梁的拓扑形貌

图5 重构的变压器梁有限元模型

将重构后的变压器梁有限元模型导入车体结构中，进行尺寸优化，选择2 种材料方案：一种材料为Q345；另一种材料为Q460。当变压器梁材料采用Q345 时，尺寸优化后得到的变压器梁尺寸见表1。

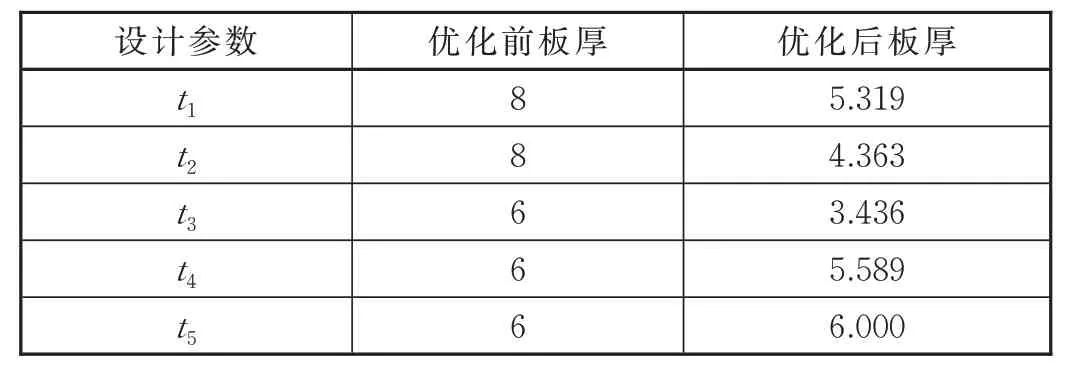
表1 局部优化前后板厚对比单位：mm

优化设计后得到的板厚数值需要调整为整数，对优化设计参数的具体数值通过向上取整进行归整，得到的设计参数见表2。

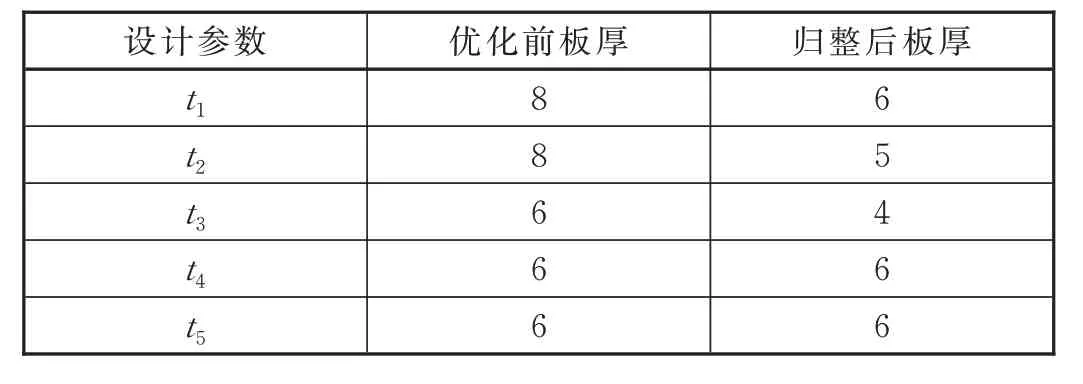
表2 局部优化后板厚归整单位：mm

将重构后的变压器梁结构各板厚度改为归整后的厚度，进行牵引工况计算，得到的Mises 应力云图如图6 所示。经过拓扑优化和尺寸优化后，变压器梁最大应力为320.3 MPa，小于Q345 的许用应力，如图6（b）所示。在满足强度要求的前提条件下，与原始结构相比，减重了137.7 kg。

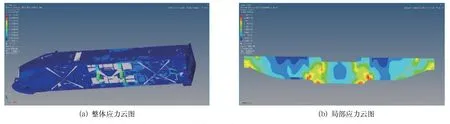
图6 牵引工况下整车和局部变压器梁的Mises 云图

当材料选择为Q460 时，尺寸优化后得到的变压器梁结构尺寸见表3，可以看到，相对于原始设计参数，优化后的变压器梁t1~t4明显减小，但是t5保持不变，这意味着t5实际上不可优化，是主承力的板件。

表3 局部优化前后板厚对比单位：mm

尺寸优化后的板厚涉及小数，因此也需对优化后的尺寸进行归整，见表4。

表4 局部优化后板厚归整单位：mm

将重构后的变压器梁结构各板厚度改为归整后的厚度，代入整车计算模型中进行牵引工况计算来校核尺寸优化后整车模型的强度，得到的Mises应力云图如图7 所示。采用优化设计后的重构变压器梁最大应力为445 MPa，小于Q460 的许用应力，如图7（b）所示。在满足强度要求的前提下，与原始结构相比，减重了234.9 kg。

图7 牵引工况下整车和局部变压器梁的Mises 云图

从尺寸优化后的减重效果可以看出，变压器梁结构的拓扑形貌对变压器梁的轻量化设计有关键影响，采用不同变压器梁得到的结构尺寸优化减重效果不同。文中得到的变压器梁拓扑优化后的形貌与原始结构的对比如图8 所示，结构几何形貌有明显改进，减重效果明显。

图8 不同拓扑形貌对比图

3 结 论

文中提出了一种拓扑优化+尺寸优化的一体化设计方法，对动力集中动车组变压器梁进行减重设计。采用拓扑优化方法对动力集中动车组变压器梁进行拓扑优化设计，对拓扑优化后的形貌进行几何重构，划分有限元网格，进行尺寸优化设计。当变压器梁材料采用Q345 时，满足强度要求的同时，结构质量由原始设计的634.68 kg 降低137.7 kg，减重21.7%。当变压器梁材料使用Q460时，满足强度要求的同时，结构质量由原始设计的634.68 kg 降低234.9 kg，减重37.0%。相关计算表明，提出的拓扑优化+尺寸优化的一体化设计方法，能有效实现动力集中动车组变压器梁的减重设计。