基于不同放牧策略对锡林郭勒草原土壤化学性质影响研究

赵琳琳,张 楠,张瀚青,胡双霞,王 岩,李金红

齐鲁工业大学(山东省科学院) 数学与人工智能学部,山东 济南 250353

放牧优化是防止草原沙漠化的关键。过度放牧因牲畜密度过大,可能导致土壤裸露面积增大,土体内水分相对运动受到不利影响,使土壤盐碱化程度加重,最终造成草原沙漠化,而适当的放牧可增强草原土壤的化学性质,促进草原生态系统的可持续发展。

针对不同放牧强度下土壤化学性质的影响,有学者们做了如下的研究。奚小艳等[1]指出,用模型模拟结合观测实验数据进行放牧对草地生态系统影响的深入机理研究是未来的研究方向。赵美曼[2]以苏尼特右旗荒漠草原为例,测定不同放牧强度下的土壤理化特性,阐明土壤可蚀性值对放牧强度的响应机制,证实土壤理化特性空间分布呈较弱与中等程度空间自相关,在不同放牧强度与区组间表现各异。许婷婷等[3]以希拉穆仁草原为研究对象,分析不同放牧强度下植物群落特征及不同深度土壤有机碳含量和密度变化,定量评估放牧对土壤有机碳的影响,发现地上生物量的减少对土壤有机碳密度的影响相对较小,土壤物理性质显著影响土壤有机碳密度的结论。于志慧等[4]以希拉穆仁荒漠草原为研究对象,分析3种放牧强度(无牧、轻度放牧、重度放牧)对0～50 cm土壤有机碳、全氮、的影响。刻画土壤有机碳含量随放牧强度增大的变化趋势。马昕昕等[5]以黄土高原水蚀风蚀交错区西部、中部、东部地区及水蚀区为研究对象,刻画3个放牧强度下退耕草地 0～20 cm 土层土壤有机碳储量的分布特征。对于若尔盖湿地不同放牧强度下的土壤化学性质,李霞[6]进行实地考察,证实轻度放牧区土壤有机质、土壤全氮含量高于强度放牧区,土壤全氮含量随放牧强度增加呈明显下降趋势。Andreza等[7]收集卡廷加生物群落不同放牧强度下的土壤数据,表明基于微生物的技术可以减轻卡廷加生物群落的土壤退化。范春梅[8]采用土壤各项指标对黄土高原丘陵沟壑区放牧林草地土壤抗蚀性能进行分析,证实土壤的有机质、全氮、水解氮和全磷含量均随着放牧强度的增加而减少。杨晶晶[9]以伊犁绢蒿荒漠为研究对象,将游牧区与定居区土壤全氮、全磷、全钾、速效氮含量进行对比,得出定居区土壤pH高于游牧区,土壤有机碳、速效磷、速效钾含量均为游牧区显著高于定居区的结论。方倩等[10]采用Meta分析和结构方程模型方法,研究不同放牧强度对于高寒草地土壤理化性质的影响强度及环境因素对平均效应值的影响过程,证实放牧增加草地土壤全碳含量,显著降低土壤全钾、全氮和全磷含量。

建立不同放牧强度下对草原土壤化学性质影响的数学模型是学者关注的重点。相较于机理分析模型,经验预测模型,包括神经网络模型等,由于具有参数较少的特点,在近十几年来已经被广泛应用在国内外的研究中[11]。马秀枝等[12]采用时间序列模型分析林火干扰对土壤化学性质的影响。黄子晨等[13]采集浙东滨海围垦农田不同土壤深度土壤样品测定有机碳含量,以未围垦的潮间带土壤作为对照,分析不同围垦时期土壤碳库组分的含量变化特征及其与其它化学性质的关系,得出随着围垦时间的增加,0～10 cm土层土壤中的可溶性有机碳均呈先减少后增加的趋势变化的结论。Turner-Meservy 等[14]使用基于前陆上暴露冰碛的时间序列,分析土壤化学性质受鸟类运动的影响,得知冰碛土壤的阳离子浓度随时间推移而增加,表明鸟类运动可以增强土壤化学性质。Cui Jun等[15]分析了水稻耕作系统和旱地种植耕作系统下的犁层土壤主要化学性质,研究土壤随开垦产生的时间序列,描绘了土壤有机碳含量随时间的变化规律。

采用整合移动平均自回归模型,给出土壤有机碳、土壤全氮、土壤碳氮比在放牧强度影响下,随时间变化的数学预测模型,具有一定的现实意义,丰富了温带草原环境下不同放牧强度对于土壤湿度影响的研究。

1 不同放牧强度对土壤化学性质的影响

1.1 土壤化学性质循环过程

土壤中各种物质和各项指标均是相互联系且相互作用。不同放牧强度下的牲畜数量不同,牲畜对牧草地采食和践踏影响草地植被覆盖率,进而影响土壤内有机碳含量。土壤有机氮作为土壤碳固机制的组成部分,受到土壤有机碳的影响。土壤微生物也参与土壤碳循环中的几个重要循环过程,如碳降解,碳固定和甲烷代谢[16]。落叶等凋零物降解产生的有机碳也会对土壤的化学性质产生影响。土壤碳元素循环机制如图1所示。

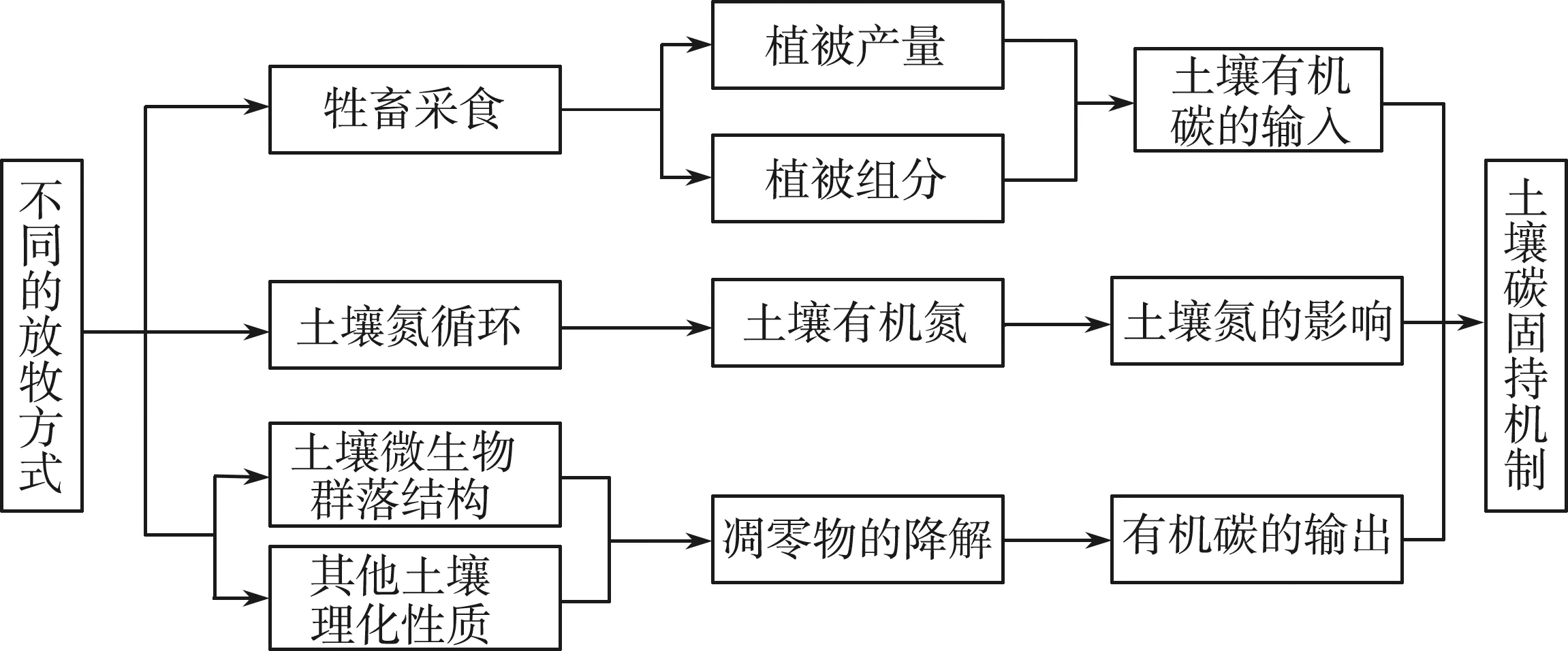
图1 土壤化学元素循环模式

1.2 主成分分析法判断因子权重

寻找主成分即寻找初始变量在各个主成分上的载荷。设代表放牧强度环境的12个放牧小区分别为ε1,ε2,…,ε12设土壤有机碳、土壤全氮、土壤碳氮比、无机碳含量和土壤全碳分别为μ1,μ2,…,μ5,设εi在μi上的载荷分别为a1,a2,…,a12。

载荷为12个放牧小区相关矩阵的5个较大的特征值对应的特征向量。Zi分别为原指标变量的第1,2,…,5个主成分,筛选土壤有机碳、土壤全氮、土壤碳氮比、无机碳含量和土壤全碳含量中受放牧强度影响前几个最大的主成分。对样本μ1,μ2,…,μ5进行标准化,记标准化后的变量为：

X=(x1,x2,x3,…,x5)′,

(1)

X满足如下的因子模型：

F1,F2,…,Fm表示标准化之后的公共因子,能作用于任何原始观测变量。

矩阵A叫做因子荷载阵,A中每一个元素aij叫因子荷载,由上式可知,因子荷载是Xi,Fj的协方差、相关系数,表示第i个变量在第j个公共因子上的负荷,因子载荷越大(aij的绝对值),说明Xi和Fj有着越强的依存关系。由表1可知,KMO统计量值大于0.5,变量间的相关程度无太大差异,数据适合做主成分分析。

4.物联网企业融资困难。作为战略新兴产业，物联网产业属于高风险、投资大的产业，需要巨额的资金投入，尤其在企业发展的初期，这往往令一般的中小企业投资者望而生畏。如果能有效解决物联网企业发展过程中企业的融资难问题，使资金能顺畅进入物联网企业，无疑，可加速物联网企业的发展。目前来看，以战略性新兴中小企业为例，其银行信贷的比例极低，仅占全部中小企业的10%左右，而在美国这一比例高达33%，资金不足成为物联网产业发展过程中无法回避的问题。

表1 KMO和Bartlett球形度检验

取内蒙古自治区锡林郭勒盟典型草原不同放牧强度土壤碳氮监测数据集[17],对放牧强度与五个指标进行主成分分析法。为消除各项指标在量纲和数量级上的差异,对指标数据做归一化处理,由SPSS软件求指标数据的相关系数矩阵,得到指标的归一化数据与相关系数。计算总方差的解释率,见表2。

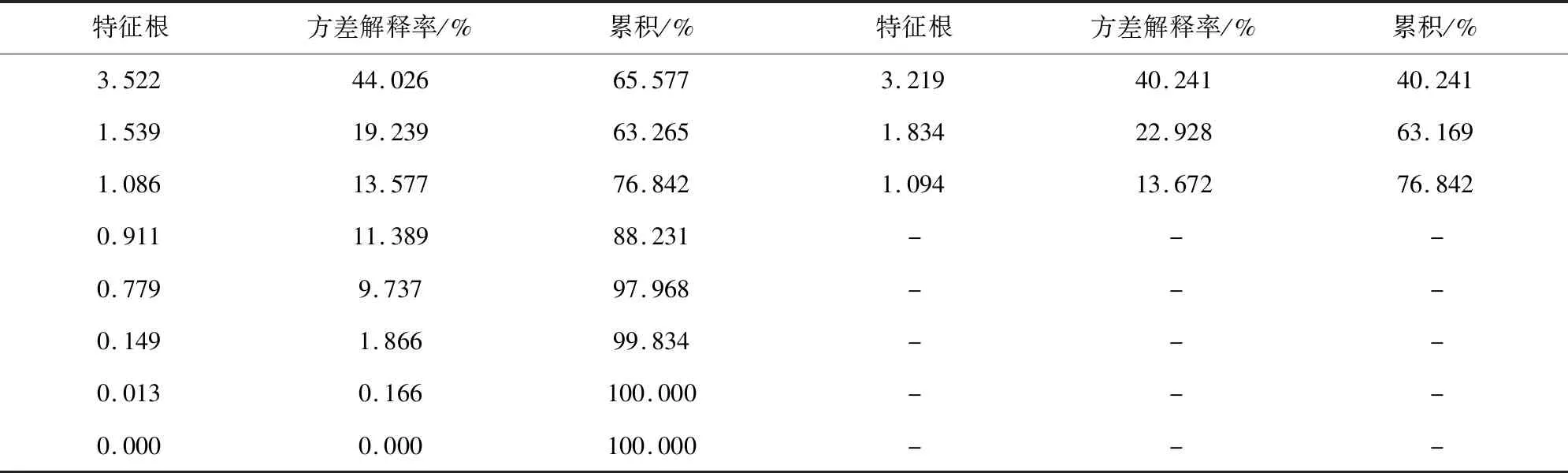
表2 总方差的解释率

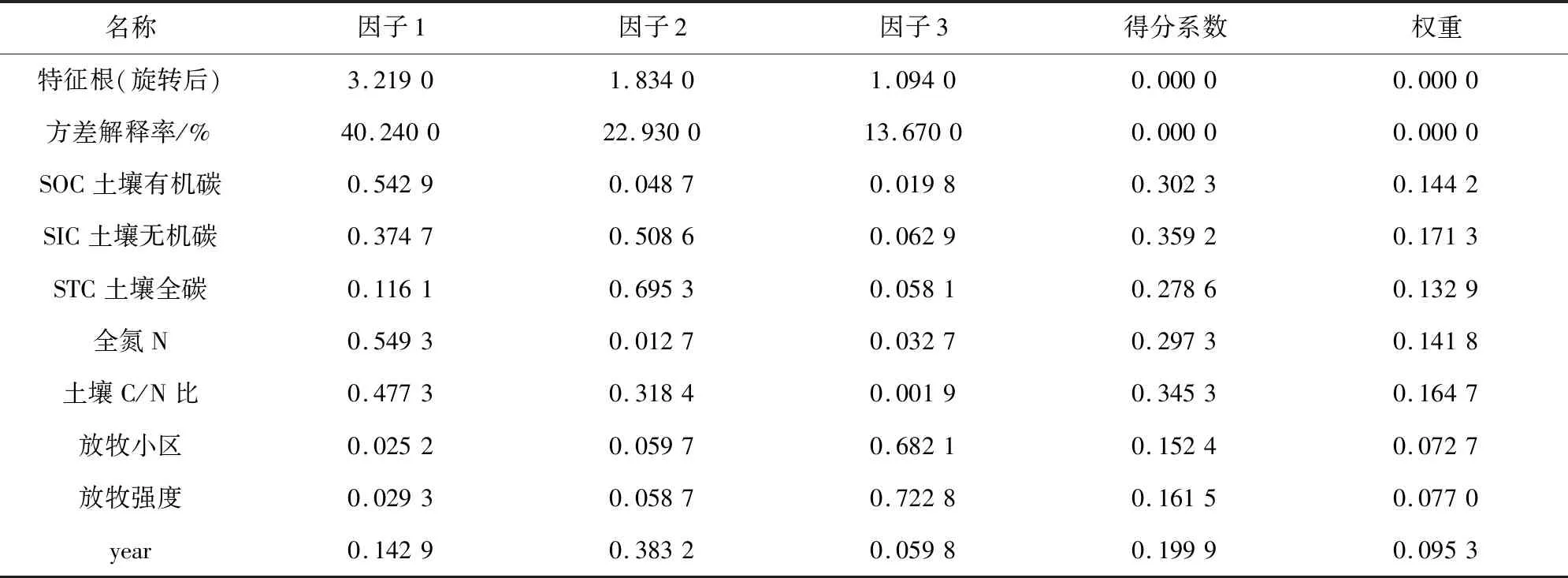
表3 线性组合系数及权重结果

表2格针对因子提取情况,以及因子提取信息量情况进行分析,从表2可知：因子分析一共提取出3个因子,特征根值均大于1,此3个因子旋转后的方差解释率分别是40.241%、22.928%、13.672%,旋转后累积方差解释率为76.842%。

综上所述,得知土壤有机碳、土壤有机碳和土壤碳氮比对环境评价影响最大,是主要因素。对土壤有机碳、土壤无机碳和土壤全氮含量进行分析验证,对数据做残差处理,增强数据的平稳性,得到脉冲函数图像,由图2可知残差处理后的数据逐渐平稳。

图2 土壤有机碳、无机碳、碳氮比对放牧强度的响应

2 ARIMA模型预测土壤化学性质

由因子分析得知,土壤有机碳、全氮含量和土壤碳氮比受放牧强度的影响最大。利用ARIMA模型描述土壤化学性质和放牧强度之间的关系。ARIMA(p,d,q)中,p为自回归项数,q为滑动平均项数,d为使其成为平稳序列所做的差分次数。针对土壤化学性质,用ARIMA模型预测的步骤如下：

(1)收集差分数据用于制作差分时序图表和检验差分平稳性。

(2)对差分非平稳性数据进行差分平稳化后的处理,确定d值。

(3)根据差分次数公式d,建立差分序列。模型进行识别和定阶,利用自相关差分函数和偏自相关方差函数确定p值和q值。

(4)模型参数的参数估计分析和适应性检验。

(5)利用ARIMA(p,d,q)模型对系统进行预测。

以土壤有机碳(SOC)含量为例,得出不同放牧强度下土壤有机碳含量随时间变化的序列图,ARIMA模型要求序列是平稳序列,因此要对数据进行平稳性分析,分析土壤有机碳含量随时间变化的自相关趋势和偏自相关趋势,见图3、图4和图5。

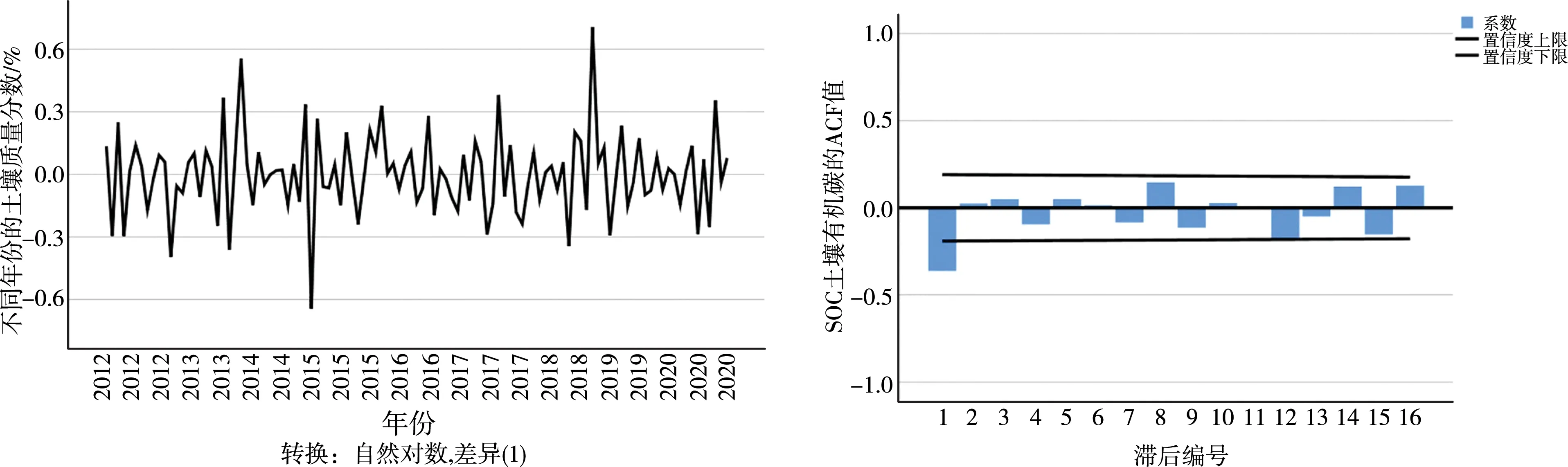
图3 SOC时序图 图4 SOC数据自相关图

图5 SOC数据偏自相关图 图6 ARIMA(2,0,0)模型拟合与预测图

从图3和图4可以看出,序列的自相关图和偏自相关图大部分编号位于置信区间内部,说明序列是基本平稳的。故可采用ARIMA模型预测2023年土壤有机碳含量。

经SPSS分析,确定p=2,q=0,d=0时的ARIMA模型最优,模型的参数统计量见表4。

表4 ARIMA(2,0,0)模型参数表

将不同时间下的土壤化学性质看作随机的序列,反映变量随时间积累受到的影响。时间序列模型不仅受影响因素的影响,也受到自身变化规律的影响。设土壤有机碳含量为y,时间为t,土壤有机碳受环境影响的最优ARIMA模型见式(3),土壤有机碳模型拟合和预测图见图6。

y(t)=3.593+0.513y(t-1)+0.250y(t-2)。

(3)

同理,土壤全氮含量的时间序列图、序列自相关图和序列偏自相关图见图7、图8和图9。由序列自相关图和偏自相关图可知,大部分编号位于置信区间内部,说明序列是基本平稳的,故可采用ARIMA模型预测2023年土壤无机碳含量。

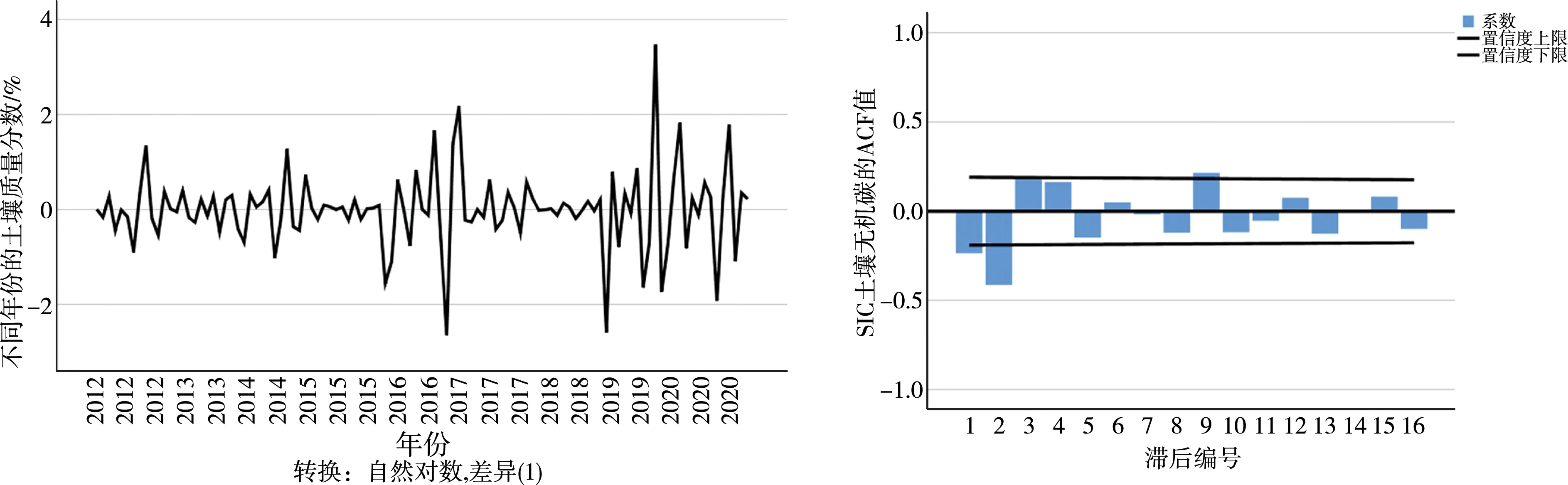
图7 SIC时序图 图8 SIC数据自相关图

图9 SIC数据自相关图 图10 ARIMA(2,1,1)模型拟合与预测图

经分析,确定p=2,q=1,d=1时的ARIMA模型最优,模型的参数统计量见表5。设土壤全氮含量为z,放牧强度为S,土壤有机碳对放牧强度的最优ARIMA模型见公式(4),土壤有机碳模型拟合和预测图见图10。

表5 ARIMA(2,1,1)模型参数表

z(t)=-0.089-0.160z(t-1)-0.353z(t-2)-0.284δ(t-1)。

(4)

土壤碳氮比的时间序列图、序列自相关图和序列偏自相关图见图11、图12和图13。由序列自相关图和偏自相关图可知,大部分编号位于置信区间内部,说明序列是基本平稳的,故可采用ARIMA模型预测2023年土壤碳氮比值。

图11 C/N时序图 图12 C/N数据自相关图

图13 C/N数据自相关图 图14 ARIMA(3,0,0)模型拟合与预测图

G(t)=2.937+0.517G(t-1)-0.023G(t-2)+0.283G(t-3)。

(5)

经分析,确定p=3,q=0,d=0时的ARIMA模型最优,模型的参数统计量见表6。设土壤全氮含量为G,放牧强度为S,土壤有机碳对放牧强度的最优ARIMA模型见式(5),土壤有机碳模型拟合和预测图见图14。

表6 ARIMA(3,0,0)模型参数

综上所给出的3个预测模型,对2023年1-12月同一放牧区内的土壤有机碳、土壤全氮、土壤碳氮比进行预测,得出2023年土壤有机碳含量、土壤全氮含量和土壤碳氮比的预测结果,见表7。

表7 土壤化学性质预测结果

3 结 论

基于ARIMA模型对锡林郭勒草原土壤化学性质进行分析,得出土壤有机碳、土壤无机碳和土壤碳氮比在不同放牧策略影响下的最优ARIMA模型分别为AR(2,0,0)、AR(2,1,1)、AR(3,0,0)。