基于神经网络辅助卡尔曼滤波算法的水质数据处理系统
李凯林,孟繁朴,任万龙,郝宗睿
齐鲁工业大学(山东省科学院) 海洋仪器仪表研究所,山东 青岛 266100
在我国农业经济中,水产养殖业一直是其中的重要组成部分,2020年我国水产品总产量达到6 549万吨,养殖产品占比达到79.8%。目前我国养殖水产品占世界水产品养殖总量的60%以上。打造智慧渔业、信息渔业成为当代渔业信息化发展的主流。
传统的水质监测需要定期采样、化验。人工进行数据分析和报告,需要大量的计算资源和时间,无法实时监测水质变化。水质数据的实时监测和优化处理一直是国内外研究的重点内容。Chowdury等[1]利用IoT技术监测河流水质数据并进行水质分析;曹守启等[2]在Chowdury基础上利用神经网络对水质模型进行了预测,但是并没有引入调节设备对水质进行调节;Geeth等[3]提出了一种基于物联网的管内水质监测方案;Haque等[4]和Patil等[5]使用ZigBee进行组网将水质数据发送到终端设备,周斌[6]也用此技术将数据上传到云端在web界面可以远程监测;Saravanan等[7]利用全球移动通信系统(GSM)对水质进行远程的监测,Ajith等[8]使用WiFi模块将水质数据上传到云端服务器实现远程监控。多数研究只是实现了对水质数据的远程监测,但对系统可能因环境干扰、系统异常等原因,造成的数据缺失和噪声增加,没有进行较好的优化处理。
对水质数据的处理,常用神经网络、聚合算法,卡尔曼滤波算法、粒子群算法等。其中神经网络结构复杂,受训时间较长,灵活性差,限制了监测的实时性。粒子群算法对于离散的优化问题处理不佳,容易陷入局部最优,降低了水质数据的精确度。卡尔曼滤波算法仅能对线性过程和测量模型进行精确的估计,在非线性场景中不能达到最优的估计效果。
针对以上问题,本文设计了基于神经网络辅助卡尔曼滤波的水质监测系统。首先对系统进行了总体设计,实现了水质数据的实时监测和调节。然后,对所获水质数据的缺失值使用格罗贝斯准则进行预处理。使用神经网络辅助的卡尔曼滤波改进型算法对所获水质数据进行降噪处理。最后,对1 d内所获的水质数据在不同算法处理下进行分析比对。
1 监测系统设计
本设计的水质监测系统主要是由感知层、网络层、应用层和调节层4层结构组成[9]。如图1所示,感知层主要进行水质数据的采集和预处理,将采集数据上传,由各监测终端完成。网络层主要是接收汇总感知层采集节点的数据信息,将数据传输至应用层和调节层的终端设备。应用层由设备终端构成,对数据进行存储、处理及分析,并且可以向云端发送控制指令。调节层主要有增氧机、抽水泵等设备,通过接收云端的控制指令来运行。本系统除采用活水测量,除定期对传感器探头进行清洗、校对等物理措施外,同时对所获水质数据进行算法优化,使水质数据更加接近真实值[10]。解决了因环境因素和系统不稳定,而导致所测水质数据出现误差和异常值的问题。
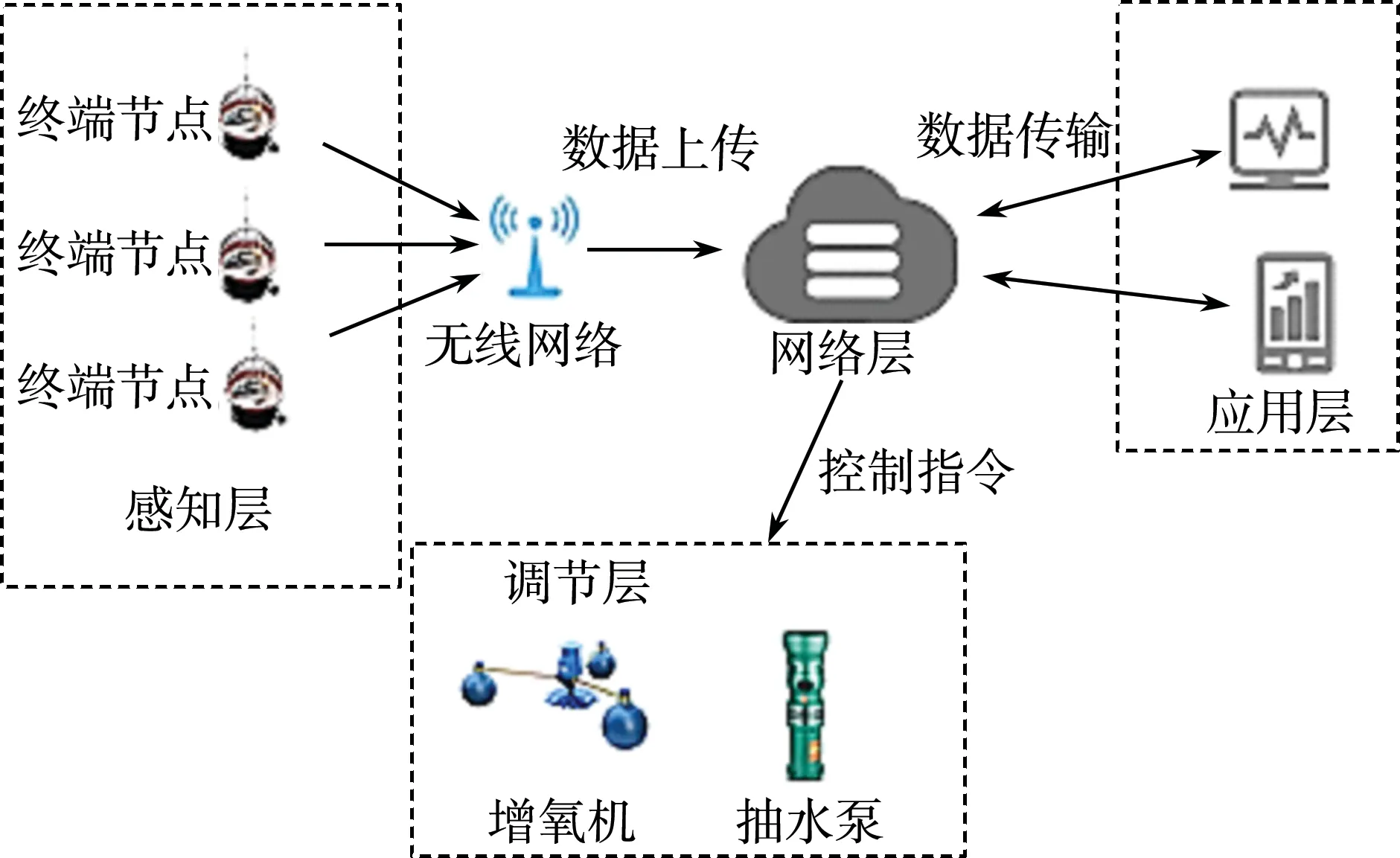
图1 水质监测系统总体框架
2 水质数据处理算法
2.1 神经网络辅助卡尔曼滤波算法
水质系统是一个时变系统,采样周期较小时,短时间内的水质数据近似线性系统。传统的卡尔曼滤波算法,虽然能够对系统状态进行最优估计,且能快速收敛,但在非线性、模型未知的场景中,达不到最优估计的效果[11]。而人工神经网络有着极强的非线性映射能力和柔性的网络结构,但其局限性是容易陷入局部最优解,收敛速度较慢[12]。为了弥补卡尔曼滤波在非线性系统中的局限性[13],国内外学者在传统算法基础上做了改进[14-15]。得到了神经网络辅助卡尔曼滤波算法。
现阶段神经网络辅助卡尔曼滤波算法主要应用于以下几个方面:在视觉跟踪领域,用于目标跟踪任务。通过使用神经网络对目标进行检测或特征提取,并将其与卡尔曼滤波进行状态估计,可以更准确地跟踪目标的位置和运动。在机器人导航和定位中,用于估计机器人的姿态和位置信息。通过结合神经网络的感知和环境信息,并将其与卡尔曼滤波的先验状态进行融合,可以提高机器人的导航精度和鲁棒性。在多传感器融合中,通过将不同传感器的数据与神经网络的输出进行融合,并利用卡尔曼滤波进行状态估计,可以提高传感器融合系统的准确性和鲁棒性。在信号处理领域,用于信号去噪、频谱估计和时频分析等任务。通过将神经网络的学习能力与卡尔曼滤波的状态估计能力相结合,可以提高信号处理的效果和性能。
现阶段该算法很少应用在水质监测领域。本文使用该算法,对水质数据进行滤波和状态估计。通过将神经网络的输出结果与卡尔曼滤波状态融合,可以提高水质数据的准确性和稳定性,实时监测水质变化。
2.2 水质数据缺失值处理
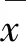
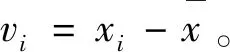
根据顺序统计原理,得到统计量g的确切分布,为:
在给定的显著水平a(通常取0.01或者0.05)后,用查表法获得格罗贝斯统计量的临界值g0(n,a),将测量顶端值与其比较[16]:
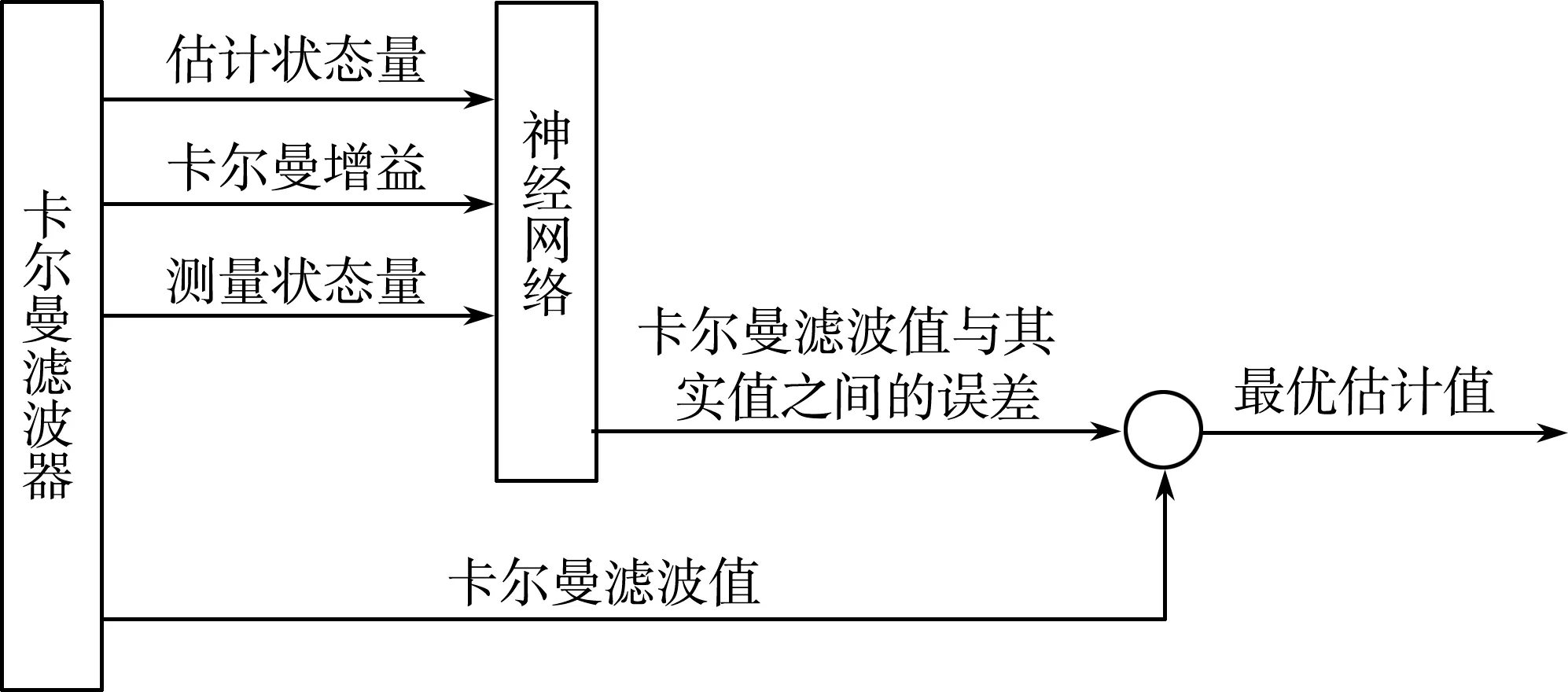
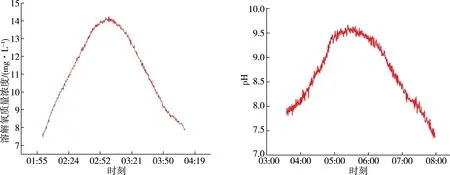
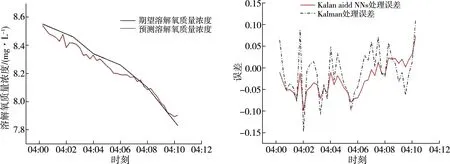
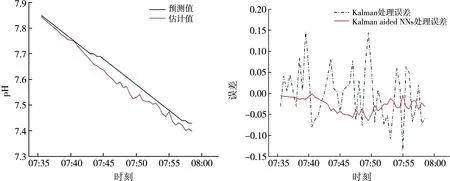
gi (4) 若式(4)不成立,则认为统计量gi带有显著差异,判定xi为误差值,将其剔除。格罗贝斯判据是一个递归算法,因此每次剔除一个可疑值之后,需要重新计算其标准差σ,重复进行判别,直至无可疑值为止。 采用自主研制的水质监测系统,搭载pH传感器,获取pH数据为基础,建立水质数据模型,分析如下。 选择状态量和观测量,可得: 式中:pt为t时刻的pH的观测值;vt为t时刻的pH变化速度;ut为t时刻pH变化速度的导数。 引入协方差矩阵表示确定估计值的不确定性: 建立卡尔曼滤波的观测模型: zt=Hxt+v, (8) 式中:zt为t时刻的观测值;H为观测矩阵;v为观测噪声。 对卡尔曼滤波进行状态更新: 式中:R为观测噪声协方差矩阵;Kt为卡尔曼增益。 噪声协方差矩阵进行更新: 建立神经网络结构,神经网络具有3层,分别为输入层、隐含层和输出层,将以下3个信号作为神经网络的输入: (2)卡尔曼滤波的增益矩阵[K]。 (3)观测方程观测值[zk]。 将卡尔曼滤波值与真实值之间的误差作为该神经网络的输出。由Hecht-Nielsn定理,只要有足够多的隐含层神经元数目,就可以无限的逼近非线性函数。本文选择一层隐含层,神经元数目为3。神经网络要通过足够多且满足工程应用精度的训练样本进行学习训练,神经网络学习过程为两部分,正向传播和误差反向传播,训练过程要遵循以下原则[17]: 神经网络辅助卡尔曼滤波器的具体结构如图2所示。经过神经网络,对卡尔曼估计值的误差进行校正之后,得到最优估计值。 图2 神经网络辅助的卡尔曼滤波算法结构图 利用pH传感器获取到的数据建立模型,采用卡尔曼滤波算法的估计状态量、卡尔曼增益和测量状态量作为神经网络的输入,卡尔曼滤波值与真实值之间的误差作为该神经网络的输出,卡尔曼滤波值消除神经网络估计的误差后,最终得出模型的最优估计值。 选取人工养殖水域,作为水质监测系统监测终端的投放点,如图3所示。对水质的溶解氧和pH数据进行获取,并设置适当的采样频率,既可降低功耗网络带宽,又可最大程度确保水质数据的准确性。 图3 水质监测系统实物图 从设计的监测系统中,选取了下午2点到4点10分共520条水体溶解氧数据(数据采样周期为1次15 s)和下午3点30分到8点的540条pH数据(数据采样周期为1次30 s)。以上数据未进行去噪处理,对所获数据进行分析。由图4和图5可知,养殖水域的溶解氧和pH数据是随时间不断变化的,即不同时段用户使用调节设备对养殖水域数据进行调节的时间也不相同。同时,由于环境等因素的影响,导致数据中的噪声较大,因此本文提出神经网络辅助的卡尔曼滤波算法进行数据的降噪处理。 图4 溶解氧监测数据变化曲线 图5 pH监测数据变化曲线 选择溶解氧数据其中的679条数据作为神经网络的训练样本,剩余41条数据进行数据的验证:如图6所示,预测溶解氧变化趋势与期望值变化趋势相同。图7所示,卡尔曼滤波算法处理后的误差值较大,神经网络辅助的卡尔曼滤波算法处理后的误差值在不同时段均比卡尔曼滤波算法处理后的误差值小。 图6 溶解氧估计值与期望值对比图 图7 Kalman aided NNs算法与Kalman算法处理结果溶解氧误差对比图 选择pH数据其中的673条数据作为神经网络的训练样本,剩余47条数据进行数据的验证,如图8所示,预测pH变化趋势与估计值变化趋势相同。图9所示,卡尔曼滤波算法处理后的误差值较大,神经网络辅助的卡尔曼滤波算法处理后的误差值在不同时段均比卡尔曼滤波算法处理后的误差值小且精度较高。 图8 pH估计值与期望值对比 图9 Kalman aided NNs算法与Kalman算法处理结果pH误差对比图 由表1可知,基于神经网络辅助的卡尔曼滤波算法对水体的测量精度有着明显的提升,相比于传统的卡尔曼滤波处理,该算法的平均绝对误差降低了20%以上,该算法的结果更加接近于真实值。 表1 Kalman aided NNs算法与Kalman算法对比 本文设计的水质在线监测系统,通过感知层终端设备采集水质数据,应用层终端设备远程监测,并可以调用调节层设备进行水质的调节。对水质数据处理,提出神经网络辅助卡尔曼滤波算法,提高了水质监测的精确度,该算法不仅对训练样本有着很高的拟合度,对测试样本也有着很高的拟合能力,更好的反应了水质数据的真实值。相比于传统的卡尔曼滤波算法,能够将溶解氧的平均绝对误差降低27%以上,均方误差降低39%以上,均方根误差降低22%以上,对pH的平均绝对误差也可降低20%以上。满足了养殖户的养殖需求,节省了人力成本和时间成本,为养殖户的科学养殖提供了数据支撑。2.3 水质数据降噪处理
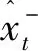
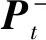
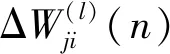

3 水质监测系统实验及分析
3.1 水质数据采集

3.2 算法验证与对比

4 结 论

