信号插值对归一化变步长FxLMS算法的影响研究

郭 畅,孙 凯,宋路昊,王希彦,王中林

齐鲁工业大学(山东省科学院) 能源与动力工程学部,山东 济南 250353

噪声污染是目前第二大环境污染,不仅影响工作生活环境,也会对人体健康造成不良影响。目前噪声控制方式主要包括被动控制与主动控制,其中被动控制方式主要通过优化结构,适用于高频段噪声控制,但该方式往往需要正交试验,实现成本较高,且通用性较差。相比之下,主动控制方式通过产生与噪声源信号等幅、反相的二次激励信号抵消源信号,适用于低频段噪声控制[1],极大地弥补了被动控制方式不足,已在社会生活、交通运输和工业生产等众多领域得到应用[2-4]。

自适应滤波算法是主动噪声控制领域的核心组成部分,其中滤波x-最小均方(FxLMS)算法,由于其结构简单、计算量小、易于实现等优点,在主动噪声控制领域得到广泛应用[5-6]。然而,传统FxLMS算法学习步长固定,难以兼顾控制效果及算法收敛速度,因此多年来国内外学者提出了多种不同变步长FxLMS(VSS-FxLMS)算法以改善该缺陷[7-9],Ma等[10]进一步提出了一种简化VSS-FxLMS算法,在不降低控制效果前提下优化了计算量。在众多VSS-FxLMS算法中,归一化变步长FxLMS(NVSS-FxLMS)算法根据滤波参考输入信号l2范数及误差信号功率调整学习步长,从而实现了在不改变算法参数前提下对不同脉动幅度信号的控制,具有广泛的适应性。Akhtar与Nishihara[11]对比了多个VSS-FxLMS算法对不同脉冲噪声信号控制效果,研究表明NVSS-FxLMS算法呈现出优异的收敛速度及控制效果。

综上所述,目前研究基于大量仿真计算,发展了不同类型VSS-FxLMS算法,以实现高控制性能、快速收敛速度及低计算成本的噪声控制,而未从源信号角度改进滤波算法。本研究从源信号角度出发,将信号插值与归一化变步长理念相结合,以提升噪声控制效果及算法收敛速度。由于信号插值数量的改变使相邻信号脉动幅度降低,从而影响算法学习步长,进而对控制效果和收敛速度造成影响。因此,研究信号插值数量对控制效果及算法收敛速度的影响,明确最佳插值数量范围,对于自适应滤波算法的发展及主动控制系统的改进具有重要指导意义。

本文首先回顾了NVSS-FxLMS算法,其次建立结合信号插值与归一化变步长理念的INVSS-FxLMS算法,最后以两种流体机械实测噪声/振动作为参考输入信号,以稳态误差及计算时间为评价指标,通过仿真计算对比信号插值数量对算法性能的影响。

1 NVSS-FxLMS算法

图1为基于FxLMS算法的单通道前馈型主动噪声控制系统图。

图1 基于FxLMS算法的主动噪声控制系统图

由图可知,噪声源信号x(n)经初级通道P(z)到达误差信号处e(n)获得d(n),次级信号y(n)经次级通道S(z)到达误差信号处获得y′(n),d(n)和y′(n)相减获得误差信号e(n)。其中,

e(n)=d(n)-y′(n)=d(n)-y(n)*s(n),

(1)

y(n)=WT(n)X(n),

(2)

式中W(n)=[w0[n],w1[n],…,wL-1[n]]T为滤波器权重,*代表卷积运算,L为滤波器长度,其更新公式为

W(n+1)=W(n)+μe(n)X′(n),

(3)

X′(n)=s′(n)*X(n),

(4)

式中S′(n)为次级通道估计模型,μ为学习步长。根据Ardekani和Abdulla相关研究[12]可知,为保证算法收敛,μ应满足

式中Δe表示次级通道的等效延迟,PX′为X′(n)的功率。当L和Δe为恒定值时,μ的合理范围由PX′所决定。

对于NVSS-FxLMS算法,μ的更新由滤波源信号和误差信号所决定,即

Ee(n)=λEe(n-1)+(1-λ)e2(n),

(7)

2 INVSS-FxLMS算法

本研究从源信号角度改进自适应滤波算法,即对采集获得的相邻源信号X(n)和X(n+1),利用线性插值在相邻两信号间插入m个数据,则公式(1)～(4)可变为

e(n)=d(n)-y(n)*s(n),

(10)

3 结果与讨论

基于Matlab构建主动控制模块,将该模块转变为FxLMS算法C程序,在此基础上进一步优化程序,构建NVSS-FxLMS与INVSS-FxLMS算法程序,采用数值计算的方式,以两种不同脉动幅度源信号进行仿真研究,通过对比稳态误差和计算时间,探究信号插值数量对NVSS-FxLMS算法性能影响。本研究中,初级通道和次级通道采用文献[13]中传递函数,滤波器长度取32,稳态误差采用平均降噪量(Averaged Noise Reduction,ANR)和频域总声压级(Total Sound Pressure Level,TSPL)表示,其中平均降噪量定义为[14]

Ae(n)=0.999Ae(n-1)+0.001|e(n)|,Ae(0)=0,

(14)

Ad(n)=0.999Ad(n-1)+0.001|d(n)|,Ad(0)=0,

(15)

式中Ae(n)和Ad(n)分别是关于e(n)和d(n)的估计。总声压级定义为

式中SPL代表某一频率下声压级,nm代表频率数量。

3.1 正弦波信号

为揭示采样率及信号插值对噪声控制效果及收敛速度的影响,以正弦波为噪声源信号进行仿真研究,其定义为

式中v(n)为方差为1的高斯白噪声信号。

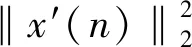
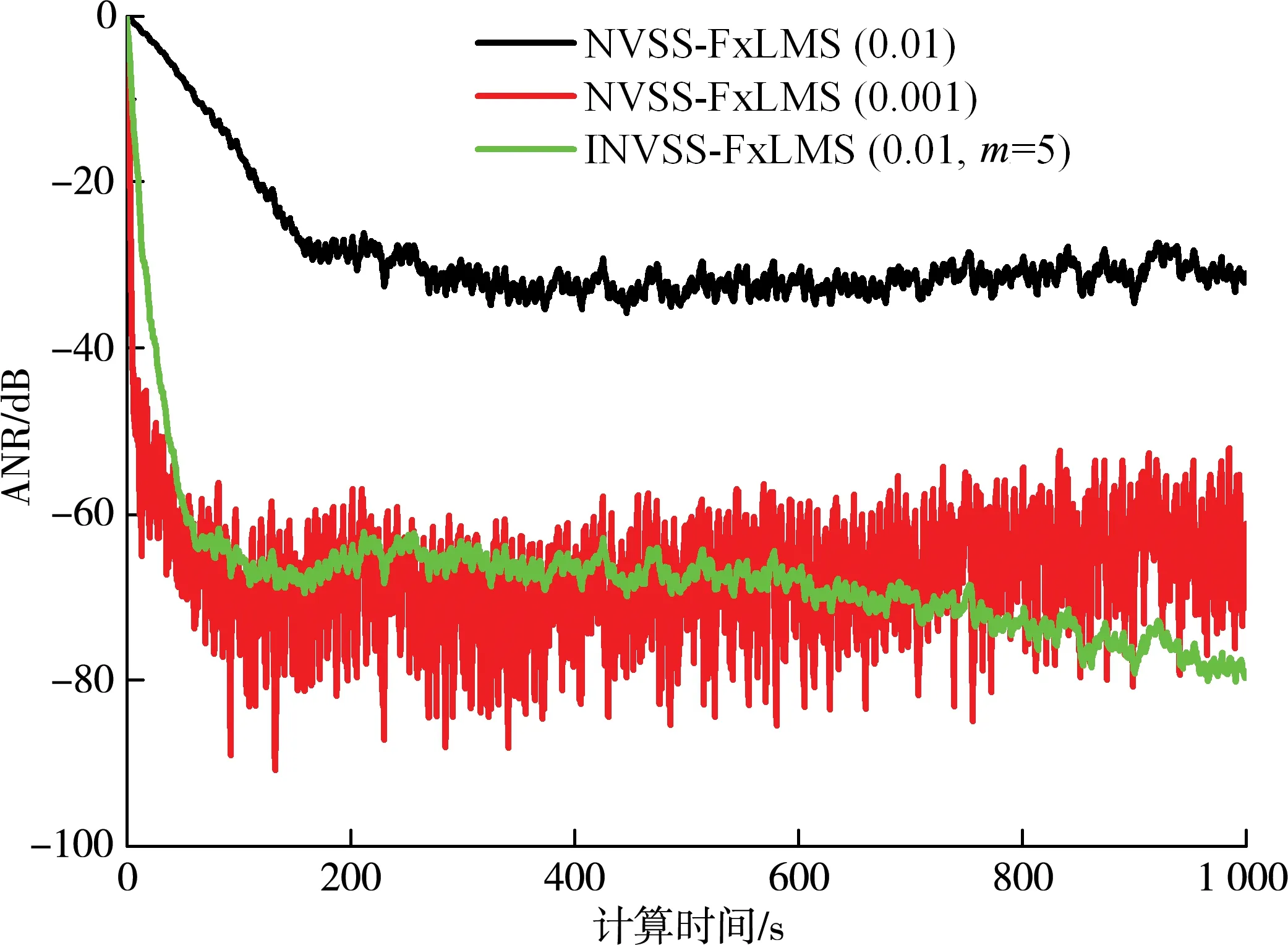
图2 不同采样率及滤波算法下ANR曲线图

3.2 离心泵噪声信号

为进一步揭示信号插值数量对算法性能影响,明确最佳插值数量,以文献[15]中离心泵流动噪声为源信号进行仿真对比研究。

图3对比了不同插值数量下ANR曲线。由图可知,在无插值情况下,算法收敛速度较慢,稳定时ANR约为-16 dB。在信号插值影响下,算法迭代计算初期,收敛速度随信号插值数量的增加而加快,而增速逐渐放缓。此外,当信号插值数量为5、8、10和13时,算法呈现稳定收敛特性,稳定时ANR分别约为-60、-62、-73和-90 dB。当插值数量为3和15时,算法则呈现发散趋势。

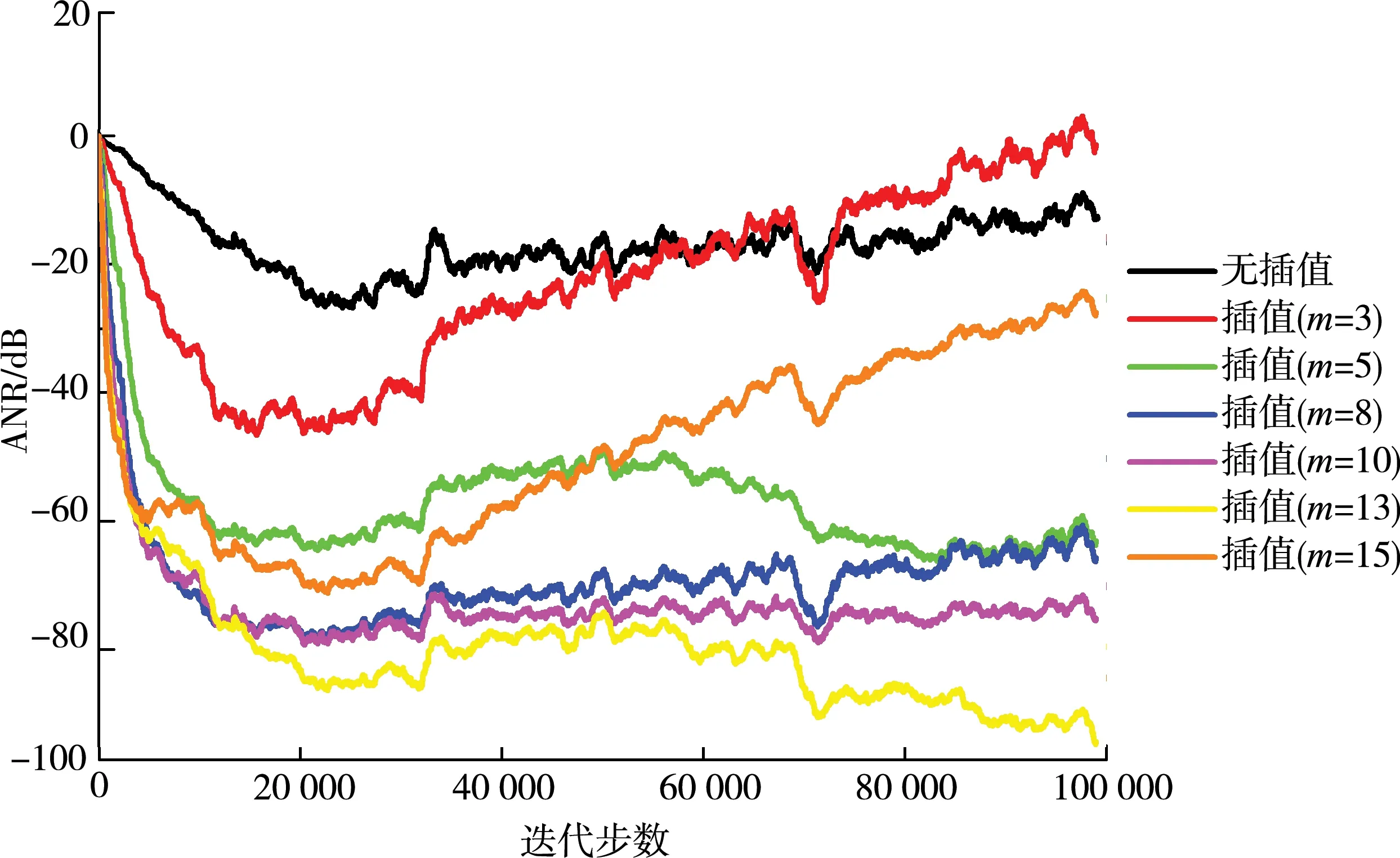
图3 不同插值数量下ANR曲线(噪声信号)

图4进一步给出了收敛条件下不同插值数量的声压频域响应特性曲线及总声压级数值。对于噪声源信号,声压级随频率的增加呈现波动上升(0～1 500 Hz),基本不变(1 500～9 000 Hz),而后波动下降趋势,噪声主要集中在9 000 Hz以内频段。在无插值情况下,当频率低于10 000 Hz时,声压级基本低于源信号声压级,而当频率高于10 000 Hz后,声压级高于源信号声压级,整体总声压级降低约3.19%。相比之下,当插值数量为5、8、10和13时,整个频段内声压级低于源信号声压级,总声压级分别降低约14.9%、15.6%、18%和21.9%。

图4 不同插值数量下声压频域响应特性

3.3 风机信号

本节以风机振动信号为例进行仿真对比研究。风机振动信号由CT1005LC振动传感器测量,采样率为6 000 Hz。

图5为不同插值数量下算法ANR变化曲线。由图可知,随着插值数量的增加,算法收敛速度逐渐加快。当插值数量为3时ANR与无插值情况相近,约为-16 dB。当插值数量为5、8、10、13和15时,ANR分别达到-25、-50、-71、-83和-85 dB,即随着插值数量的增加,ANR增量逐渐减小。

图5 不同插值数量下ANR曲线(振动信号)

图6给出了不同插值数量下振动加速度频域响应特性图,振动加速度级由式(14)计算。由图可知,不同插值数量下振动加速度级均呈现以离散特征频率为主的频域响应特性。此外,在无插值情况下,振动加速度级降低约5.48%,当插值数量分别为5、8、10、13和15时,振动加速度级降低约11.1%、15.4%、20.4%、21.9%和22.5%。

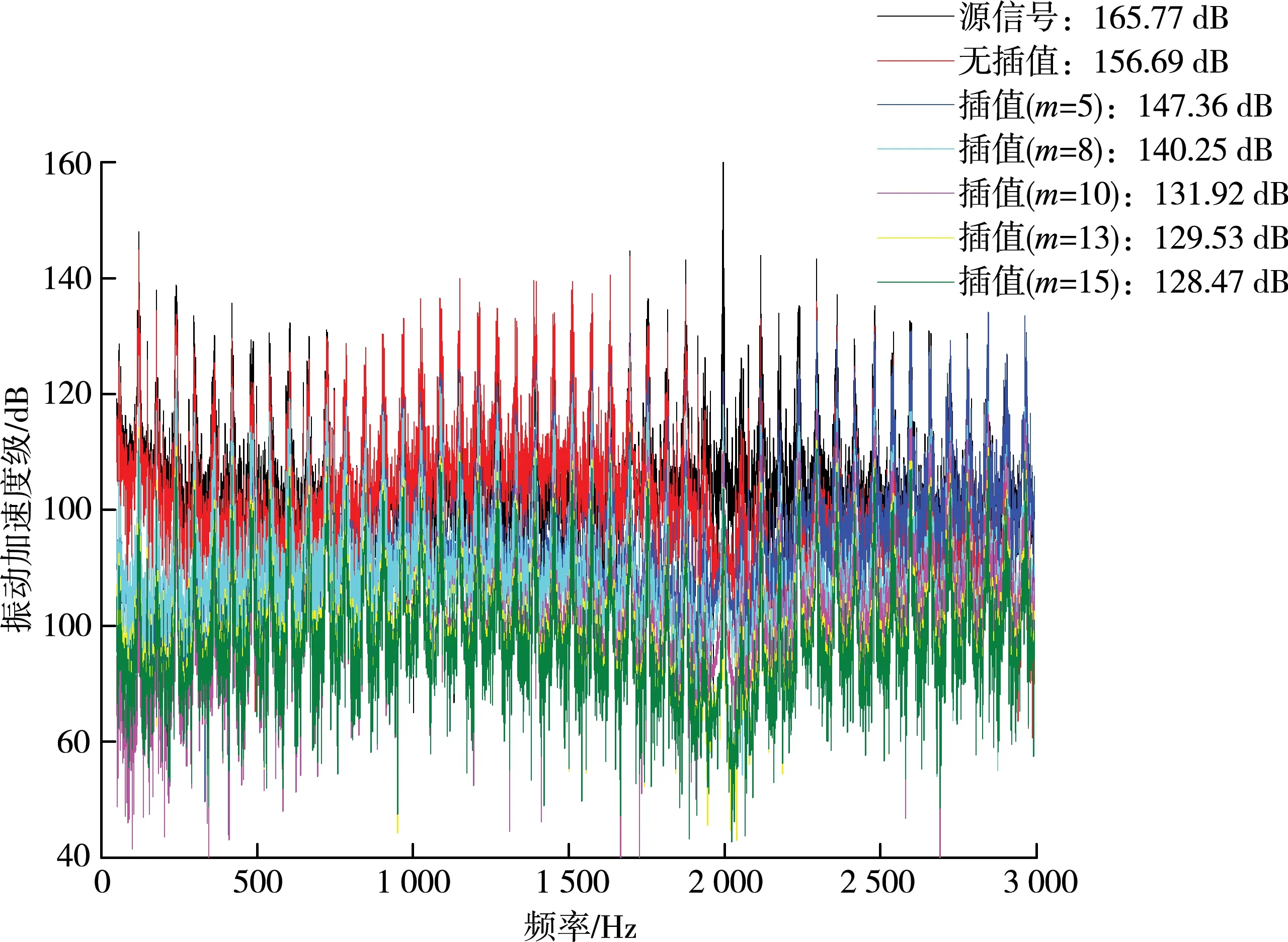
图6 不同插值数量下振动加速度频域响应特性

3.4 计算成本分析

信号插值使数据量成倍增加,从而导致算法计算成本升高,因此经过多次仿真,本节对比了不同插值数量下离心泵噪声信号10万次迭代步骤的计算平均时间,如图7所示。整体而言,信号插值后计算时间增长较少,当插值数量为13时,计算时间相对于无插值情况增长约12.7%。此外,随着插值数量的增加,计算时间基本呈线性增长趋势,当插值数量为5时,计算时间相对于无插值情况增长较多,约4.5%,随后计算时间增量基本保持在2.6%左右。

图7 不同插值数量下计算平均时间对比

结合上述噪声、振动信号控制研究可知,信号插值可加快滤波算法收敛速度并提升控制效果,同时插值数量存在最佳范围,当插值数量为10左右时,控制效果较好,总声压级/加速度级相对源信号降低率达18%,而计算时间相对无插值情况仅增长约9.6%。

4 结 论

本文建立了信号插值与归一化变步长理念相结合的INVSS-FxLMS滤波算法,并通过仿真研究了信号插值数量对控制效果及算法收敛速度的影响,研究结论如下：

(1)高采样率和信号插值均可提升滤波算法的控制效果及收敛速度,然而信号插值计算量小于高采样率计算量,因此信号插值与归一化变步长理念相结合可在控制计算量的基础上改善算法收敛特性及控制效果。

(2)信号插值可使相邻信号脉动强度降低,即滤波源信号功率减小,使得算法合理步长增加,同时滤波源信号l2范数减小,因此算法学习步长增加,收敛速度加快。同时,更多源信号数据用于次级信号计算,因此控制效果提升。

(3)随着插值数量的增加,迭代初期算法收敛速度加快,而增速逐渐放缓。信号插值数量存在最佳范围,当插值数量为10左右时,算法性能较好,总声压级/加速度级降低率达18%,计算时间仅增长约9.6%。