多通道Laplacian矩阵融合的超图直推学习模型
徐良奎,杨 哲,吴国荣,赵 雷
1(苏州大学 计算机科学与技术学院,江苏 苏州 215006)
2(江苏省计算机信息处理技术重点实验室,江苏 苏州 215006)
3(江苏省大数据智能工程实验室,江苏 苏州 215006)
4(高等计算医学实验室 北卡罗来纳大学教堂山分校,教堂山 美国 NC 27599)
1 引 言
在数学上,图(Graph)是一种重要的非欧几里得数据模型,是表示对象间关系的一种方式.许多重要的机器学习问题可以用普通图模型来求解,如社交网络、基因(组)数据、网页排序等问题[1].但现实世界中对象之间往往是复杂的一对多、多对多的关系[2],如文献引用,一篇论文可以引用多篇论文,也可以被多篇论文引用.用普通图解决此类问题时,会造成信息的损失.因此出现了普通图的变体—超图(Hypergraph)模型[3].超图的一条边可以包含多个顶点,称之为超边.由于超图可以更好地描述对象间的多元信息,具有更强的高阶非线性关系的表示能力,近年来基于超图的直推学习成为机器学习领域的一个研究热点,在物体分割[4]、基因分类及医学诊断[5]、图像分类[6]、推荐系统[7]等方面都取得了较好的效果.
目前针对超图直推学习模型的求解主要有两种方法.一种方法是将超图结构扩展为普通图结构,然后使用普通图的方法去求解超图问题,代表性的方法有星扩展[9]、团扩展[10]、线扩展[11]等.由于对普通图的研究较为成熟,用普通图求解超图问题可选择的方法也较多,缺点是超图扩展为普通图的过程中会带来信息损失,将顶点间多元关系变成二元关系,不利于超图问题求解.另一种方法是直接针对超图结构及其Laplacian矩阵,求解最优的超图切,即得到超图Laplacian矩阵的若干切向量,将超图分为不同的子集以便分类或者聚类.本质上这是一个组合优化问题,代表性方法有周氏标准化Laplacian[3]、超图直推学习正则优化[6,12,13]、超图多模态结构[8]、超图深度学习[15]等.这类方法直接针对超图结构进行Laplacian矩阵求解和优化,避免了结构转换的信息损失,也是本文的研究方法.
本文提出多通道Laplacian矩阵融合的方法,优化超图直推学习模型的求解过程,提高模型分类效果.具体工作和创新包括:
1)在构建超图时,提出一种超图结构扩张的方法.将基于不同特征提取方法构造的异构超图的关联矩阵和权重矩阵进行拼接,得到扩张的超图结构后进行模型求解,完成数据分类.实验结果表明,扩张后的超图结构,可以有效提高超图直推学习模型的分类性能.
2)为了缓解异构超图结构扩张后,矩阵维度过高所带来的计算开销问题,提出多通道Laplacian矩阵融合的方法.在扩张的超图结构上,先分别计算出每个超图结构对应的Laplacian矩阵,将多个计算通道得到的Laplacian矩阵加权累加后,再进行数据分类.实验结果表明,多通道Laplacian矩阵融合方法,既能减少超图结构扩张后的计算开销,又进一步提高了模型分类的性能.
3)在图像分类和文本分类数据集上,将本文2种方法与3种传统分类模型,1种普通图模型和3种超图模型进行对比.实验结果表明,本文提出的两种方法均能取得较好的分类性能.
2 相关工作
自从Zhou等人首次提出了超图直推学习模型[3],并使用“Markov随机游走”的思想对模型进行解释后,近几年对超图问题的求解主要有两种方法:超图扩展和超图分割.
超图扩展的方法,一般是将超图结构扩展为普通图结构,然后使用普通图的方法去解决超图问题.Hu首先提出星扩展的方式[9],对超图的每条超边引入一个新节点,新节点与超边内每个顶点都有一条边相连.这种方式没有考虑到同一超边内顶点间的连接关系.后来Agarwal提出团扩展的方式[10],把每条超边视为一个全连通子图,虽然建立了同一条超边内顶点间的联系,但仍不能全面表达超边间顶点的连接信息[11].为了进一步减少扩展过程中的信息损失,Xia于2020年提出了线扩展的方式[15,17],将超边与每条超边内部的节点看作一个新的顶点.这种方式最大程度上保留了顶点和超边间的连接信息,但是在处理某些问题上仍会造成信息损失,如法诺平面问题[18].为了避免上述结构转换带来的信息损失问题,Gao引入了超图多模态模型[8],将不同的模态对应一个带权子超图,然后将所有的子超图一起训练参数.这种方式待优化的参数过多,给训练带来了很大的时间开销.因此,Feng于2019提出多模态超图关联矩阵扩展的方式,在优化超图结构的同时降低了机器学习的时间开销[16].但这种扩展方式仅仅将超图关联矩阵进行拼接,没有考虑超边权重矩阵对超图模型的影响.
超图分割的方法,主要是基于超图Laplacian矩阵去求解最优的超图切.为了优化超图Laplacian权重矩阵,Chen等人将L2正则化用于优化超图直推学习模型的权重参数[6,12].Chen和Luo分别使用交替最小二乘法[12]和坐标下降[13]的方法去优化权重参数,希望得到的更高质量的Laplacian矩阵,虽然一定程度上提高了模型的性能,但是受限于超图结构的质量.Guo利用随机矩阵扩散的思想去优化超图Laplacian最优切,但受制于单一超图结构,且需要优化额外的目标函数,时间成本过高[19].后来在超图直推学习模型的基础上,Zhang等人提出超图归纳学习模型,利用类别投影矩阵得到样本的类别标签[20].虽然降低了一定的时间复杂度,但是模型训练时没有使用所有数据集的信息,分类性能不如超图直推学习模型.
综上所述,现有超图模型求解方法都存在一定的局限性,有些方法丢失了超图结构中蕴含的重要信息,有些方法仅仅是对Laplacian矩阵参数求解过程的优化,并没有打破单一超图结构的限制,并且容易带来较大的时间开销.本文提出的超图扩张和多通道Laplacian矩阵融合的方法,不仅了融合了多种异构的超图结构,提升了超图直推学习模型的分类效果,还降低了模型的时间开销.
3 基于Laplacian矩阵融合的超图直推学习模型
3.1 超图直推学习模型
超图模型(图1(a))一般表示为三元组G=(V,E,W),其中V={v1,v2,…vn,}为超图顶点集,每一个样本对应V中的一个顶点,E={e1,e2,…em,}为超边集.超图的每条超边ej(1≤j≤m)能连接多个顶点vi(1≤i≤n),因此超边与顶点的连接关系可以用关联矩阵H∈Rn×m来表示,见图1(b).H中每个元素h(vi,ej)的定义为:
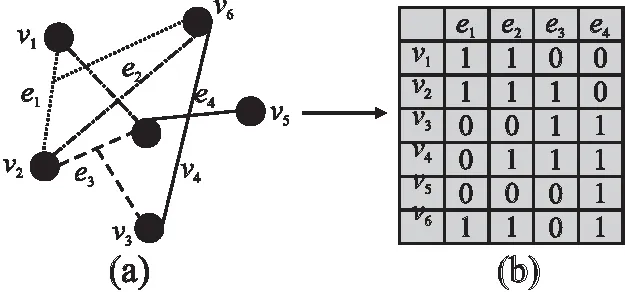
图1 超图与超图关联矩阵Fig.1 Hypergraph and incidence matrix
(1)
每条超边ej被赋予一个权重w(ej),w(ej)由高斯核方法计算得到[14],如式(2)所示.其中dis(vi,vk)(1≤i,k≤n)表示顶点vi,vk间的欧式距离,σ表示所有顶点间距离的均值.
(2)
定义权重矩阵W∈Rm×m,W是一个对角阵,对角线上的元素为每条超边的权重w(ej)(1≤j≤m),如式(3)所示:
(3)
在超图中,每个顶点vi的度d(vi)定义如式(4)所示:
(4)
定义超边ej的度δ(ej)为这条超边包含的顶点个数,如式(5)所示:
(5)
定义两个对角阵Dv∈Rn×n、De∈Rm×m,类似公式(3)它们的对角元素分别是超图中每个顶点的度d(vi),每条超边的度δ(ej),算法1总结了上述超图构建算法的流程描述.
算法1.超图构建过程描述
Step1.数据预处理,得到样本特征X={x1,x2…xn}
Step2.样本点对应顶点,得到顶点集V={v1,v2,…vn,}
Step3.设置超边顶点个数K(K值不宜过大,可使用网格搜索算法等)
Step4.使用欧式距离计算顶点间相似度Eud(vi,vj)
Step5.根据Step 3得到超边集E={e1,e2…em}
ei={j|TopK-Eud(vi,vj)}(j≠i)
Step6.计算顶点的度、超边的度等
超图直推学习模型问题的正则优化目标函数如式(6)[6,12]:
(6)
其中λ和μ是两个正则化参数,用来平衡(6)中各项.对于一个c分类问题,F∈Rn×c是最终求解的切向量矩阵,包含预测的样本类别信息.模型学习阶段同时使用标记数据和未标记数据,Y∈Rn×c是含有真实样本标签的向量,若顶点vi属于第k(0≤k≤c)类,则Y(vi)[k]=1,Y(vi)[p]=0(0≤p≤c且p≠k).θ(F)是经验损失函数,Ω(F)是标准化损失函数,定义分别如式(7)和式(8)所示:

(7)
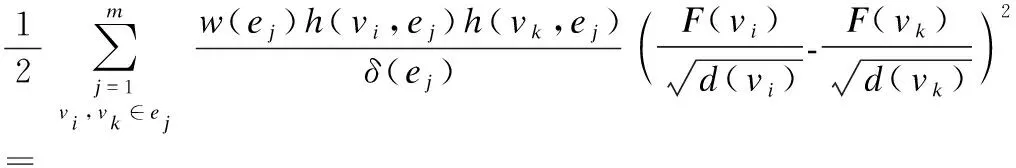
(8)
公式(8)中,L为超图标准化Laplacian矩阵:
(9)

(10)
由于超边权重W可以反映超边的重要程度,因此训练阶段求解F的同时迭代优化W.由于目标函数(6)单独相对于W或F是凸函数,可采用两种交替优化的方法去优化W和F,分别是交替最小二乘法和坐标下降法.

(11)
第2步,固定F优化W,关于W的损失函数为:
(12)
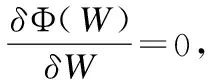
(13)
第3步,重复前两步,直至W和F趋于稳定.

(14)
(15)
得到的F即为最终的标签向量,顶点vi的类别对应index(max(F(vi))),即F(vi)最大值的下标.
3.2 超图Laplacian矩阵
超图直推学习模型的N分类问题,本质上是N路超图切问题,再加上一个分类器将样本分类.而N路超图切的解,就是超图Laplacian矩阵的N个特征向量[3].这是由于超图Laplacian矩阵揭示了超图的谱属性[3,21],即Laplacian矩阵的特征值和特征向量属性.因此,若Laplacian矩阵能描述更全局、深层次的超图结构信息,超图切的准确度就会提高,相应的分类性能也会提高.Zhou等人首次提出超图直推学习模型[1],并使用Markov随机游走的思想,从概率的角度对超图Laplacian矩阵的谱属性进行了分析.结果表明,超图直推学习模型的目标函数式(6),是经过Markov随机游走过程推导而来的[1].超图上每个顶点Markov随机游走的概率满足如下规则:给定当前的位置vi∈V,首先在所有与顶点vi以一定概率相关的超边中选择一个超边ej,然后均匀随机选择一个顶点vk∈ej(k≠i).公式(15)给出了超图顶点Markov随机游走的概率,公式(16)是对公式(15)运算过程的矩阵化表达.
(16)
(17)
令S表示超图顶点集V的一个子集,Sc是S的补集,超图G的一个切就是将超图分为S和Sc两部分.VolS表示集合S的体积,∂S是被切割超边的集合,∂S={ej∈E|ej∩S≠φ,ej∩Sc≠φ}.公式(17)和公式(18)定义了VolS和Vol∂S的计算方式:
(18)
(19)
公式(19)、公式(20)证明了Markov随机游走的平稳分布为π(vk)[1].
(20)

(21)
由公式(15)、公式(16)可以看出Markov随机游走的过程,与公式(9)超图标准Laplacian算子L是一致,若V是P的特征向量,那么V也是L的特征向量.Laplacian矩阵可以看作超图结构经过随机游走后的表达.超图切的目标函数为式(21),公式(19)~公式(23)证明了Markov随机游走的最小切,就是使得连接不同聚簇的边的相似度最小(顶点转移概率最小),而同一聚簇内部顶点转移概率最大,并逐渐趋向于一个稳态分布的分区.由于直接求解式(21)比较困难,因此将其转换为式(6)对应的基本损失函数式(8),即argminΩ(F).argminΩ(F)的解为超图Laplacian矩阵N个最小非零特征值对应的特征向量,即为超图Laplacian矩阵的谱属性.因此Laplacian矩阵对求解超图问题非常关键.

(22)
(23)

(24)
3.3 超图Laplacian优化
3.3.1 超图结构扩张
根据公式(9)可知,超图Laplacian矩阵与超图关联矩阵H和权重矩阵W有关,本节主要讨论如何优化超图结构以得到高质量的超图Laplacian矩阵.一般在构造超图结构,先提取对象的向量化特征,然后根据顶点相似度,将相似的顶点连接在一条超边上,最后用点-边关联矩阵H和权重矩阵W表示超图模型的基本结构.超图之所以能比普通图刻画更多的信息,主要是关联矩阵H和W表达了更多的顶点-顶点间、顶点-超边之间的关系.
根据公式(15),超图中每个顶点随机游走的概率是以超图关联矩阵为基础进行计算的,在这个过程中超图顶点可以融合到更多邻域信息,以此来提高顶点分类的准确性.Markov随机游走具有传导性,合理的关联矩阵扩张能使Markov随机游走的过程中,不仅包含顶点的邻域信息,还有机会接触更远的顶点以探索全局信息,因而有利于超图结构全局特征的表达,最终得到融合更多全局信息的超图Laplacian矩阵.本文采用拼接的方式去扩张超图结构,将不同的关联矩阵H拼接在一起后,使得原来没有连接的两个顶点,经过不同的短路组合又连接在一起,这可以达到随机矩阵P“扩散映射”的效果[19].同时能够在异构的超图空间中发现不同尺度的几何结构,相比原始空间更能够保持超图几何结构的全局性.
由于不同的特征提取方式得到的特征空间不同,对应的超图结构也不同,所以关联矩阵拼接可以看作是一种异构超图结构的扩张.见图2,不同的特征提取方法会得到对应的超图关联矩阵Hi∈Rn×m,之后将关联矩阵H1,H2,…,Hk拼接,则新的关联矩阵H′=[H1‖H2…‖Hn]∈Rk×(n×m).因此超图顶点概率转移公式可以改写为式(24),其矩阵表达方式见式(25):
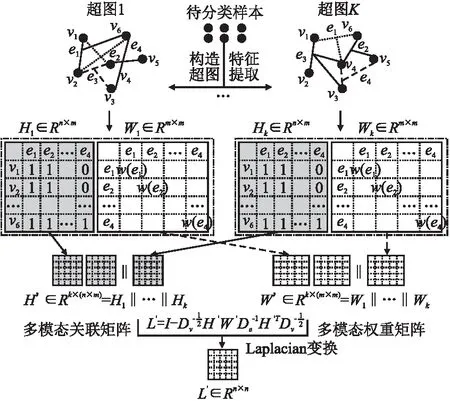
图2 异构超图结构扩张(‖表示拼接操作)Fig.2 Structural extension of heterogeneous hypergraph
(25)
(26)
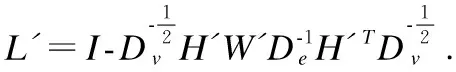
3.3.2 多通道Laplacian矩阵融合
图3描述了多通道Laplacian矩阵融合的主要过程.由于不同的超图结构对应的Laplacian属性不同,本文在构造出不同超图结构关联矩阵Hi的基础上,直接计算每个Hi对应的Laplacian矩阵Li,Hi计算得到Li的过程看作一个计算通道,多个Hi即对应多个通道,之后进行加权求和作为全局超图Laplacian几何结构的表征矩阵,记为L″.本文假设每个Li对全局超图结构的表达是相同的,即:
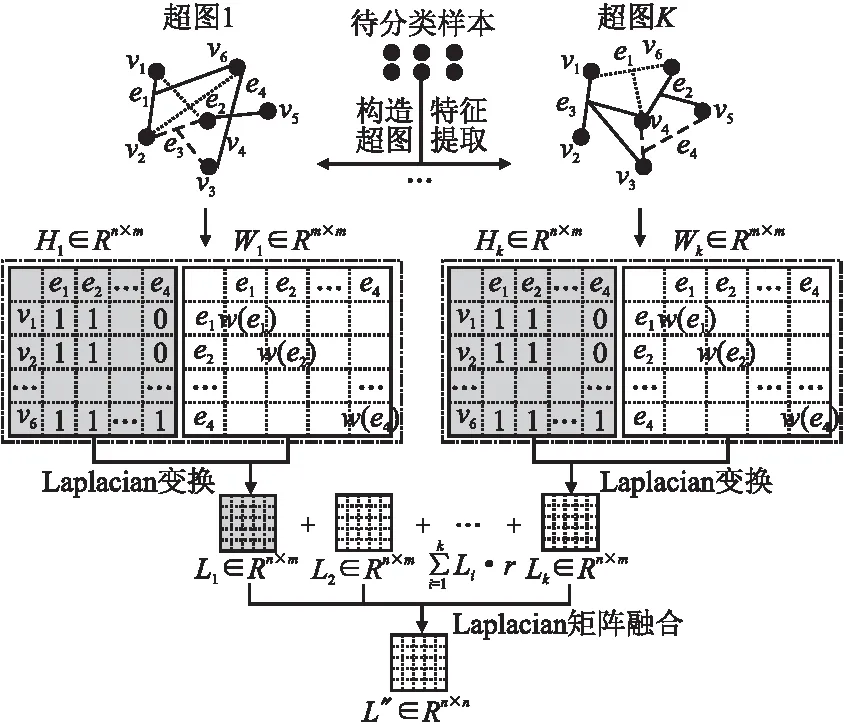
图3 多通道Laplacian矩阵融合Fig.3 Multi-channel Laplacian matrix fusion
(27)
K代表融合Laplacian矩阵的通道个数,之后基本的损失函数Ω(F)就可以重写为如下:
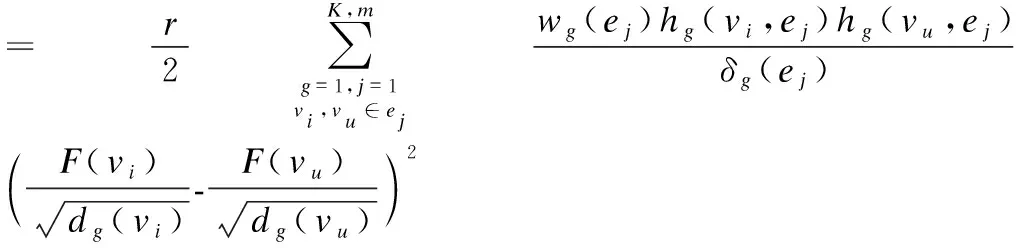
(28)
图3中,每个通道计算出的Laplacian矩阵包含了这个超图结构所对应的深度信息,而多通道在广度上将这些深度信息融合起来,使最终的Laplacian矩阵包含的信息更全面,质量更高.同时相比3.3.1提出的异构超图结构扩张方法,多通道Laplacian矩阵融合方式并没有增加矩阵的维度,仅仅是多了每个通道计算Laplacian矩阵的时间,解决了关联矩阵拼接的高维度问题.和3.3.1相同,得到高质量的Laplacian矩阵后,使用交替最小二乘法去求解目标函数.根据表6的实验数据,多通道融合方式的时间成本要远小于异构超图结构扩张方式,并且多通道Laplacian矩阵融合方式的分类性能更高.
4 实验与分析
4.1 实验环境
本文的实验主要针对超图直推学习模型的分类问题,并与一些经典分类算法、普通图和超图模型做了对比,实验环境如下:
1)硬件配置
使用GPU集群,可用资源为CPU 96Core,GPU 2Core GeForce_RTX_2080_Ti /2Core Tesla_v100_ sxM2_32GB,内存512GB,存储空间500GB.编程语言:Python.
2)实验参数
使用KNN的方式构造超边[22,28],即超边包含的顶点是中心顶点和离它最近的K个顶点.除了表2 SIFT和表3 Jaccard直接计算样本间的相似度外,其余实验均是得到样本特征后,统一使用欧式距离衡量样本间相似度,之后基于样本间相似度构造超图结构.
3)数据集
表1记录了数据集的详细信息,为了更好的验证本文提出的模型性能,选取4个不同领域的数据集来进行实验.所有的样本数都含有标签信息,将每个数据集划分为训练集和测试集两部分,训练集使用标签信息,测试集不使用标签信息,直推学习过程中测试集和训练集同时参与训练.训练结束后模型会输出测试集的预测类别,之后使用评价指标衡量模型预测的性能Cat&Dog:图像数据集,来源于Kaggle官网[23],包含了猫和狗两部分图像,常用于分类任务.

表1 实验数据集Table 1 Data set
Cifar10:图像数据集,是一个用于物体识别和分类的经典计算机视觉数据集[24],所包含的图像是RGB彩色图,共有10个类别.
Ctrip:文本数据集,使用的是2018年携程网国内酒店的评论数据[25],每条评论都已经标注好情感方向,如好评或者差评.
Spambase:数值型数据,由UCI官网[26]提供的处理后的垃圾邮件数据集,主要用于垃圾邮件的识别分类.
4)评价指标:
本文使用的分类评价指标有准确率(Accuracy),精确率(Precision),召回率(Recall)和F1,计算公式如公式(28)~公式(31)所示.其中TP表示实际为正被预测为正的样本数量,FP表示实际为负但被预测为正的样本数量,FN表示实际为正但被预测为负的样本的数量,TN表示实际为负被预测为负的样本的数量.
准确率:预测样本中分类正确的样本占总样本个数.
(29)
精确率:预测为正的样本中实际也为正的样本占被预测为正样本的比例.
(30)
召回率:实际为正的样本中被预测为正的样本所占实际为正样本的比例.
(31)
F1:精确率和召回率的调和平均值,衡量分类模型的稳健性.
(32)
5)实验设置
4.2节在图像和文本数据集上通过不同的特征处理方式构造异构超图结构,根据超图直推学习模型分类的结果考察异构超图结构的质量.
4.3节在4.2基础上研究不同超图结构组合对超图结构扩张法的影响.
4.4节首先在文本和图像数据集上研究不同超图结构组合对多通道Laplacian矩阵融合法的影响,之后在4个数据集上比较两种优化方法,验证多通道Laplacian矩阵融合法的分类性能优于超图结构扩张法和正则优化后的超图直推学习模型.
4.5节进一步在文本和图像数据集上将两种优化方法与其余一些模型做对比,证明本文提出的多通道Laplacian矩阵融合法有较好的分类能力.
4.2 异构超图结构分类实验
不同的特征处理方式得到的数据特征空间不同,对应的超图结构包含的信息也不同,因而对应的超图结构质量也不同.本节主要针对图像和文本数据考察基于不同特征提取方式构造的超图结构,对超图直推学习模型分类精度的影响,并为4.3和4.4节实验提供数据参考.在处理超图模型分类任务前,对于图像和文本数据,首先要提取数据样本的特征,之后在此基础上计算样本间的相似度去构造超边及超图关联矩阵.
表2中PHA、VGG、ResNet分别指使用感知哈希[27]、VGG[29]和ResNet[30]方法提取图像特征.SIFT指SIFT提取图像关键点后用关键点匹配数目表示样本之间的相似度.HSIFT、HVGG指图像经过色差直方图预处理之后分别使用SIFT[31]和VGG方法提取图像特征.RVGG指将图像Soble锐化增强边缘信息后[32],使用VGG提取图像特征.
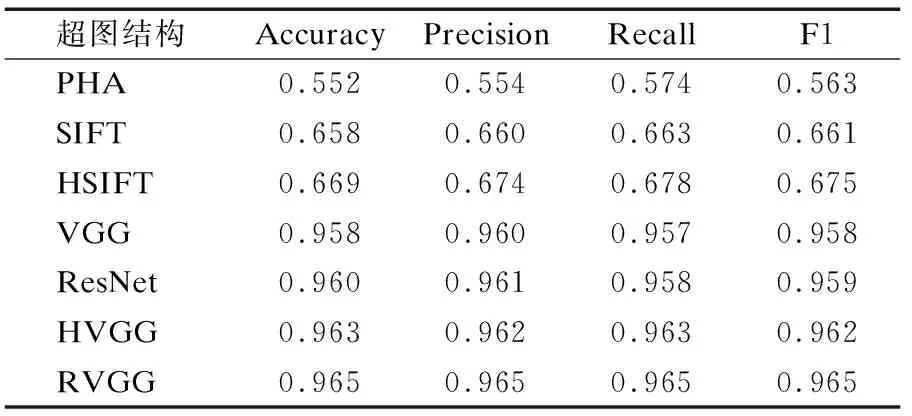
表2 异构超图结构分类实验-Cat&DogTable 2 Heterogeneous hypergraph structure classification experiment-Cat&Dog
表3中TF-IDF、LSI、Word2Vec[33]、Doc2vec[34]指使用这些方法提取文本数据的特征.在提取完数据样本特征之后,使用欧式距离计算样本间相似度,Jaccard表示使用Jaccard计算方法去衡量文本样本之间的相似度.在得到样本间相似度之后,根据KNN的方式去构造超边及超图结构.
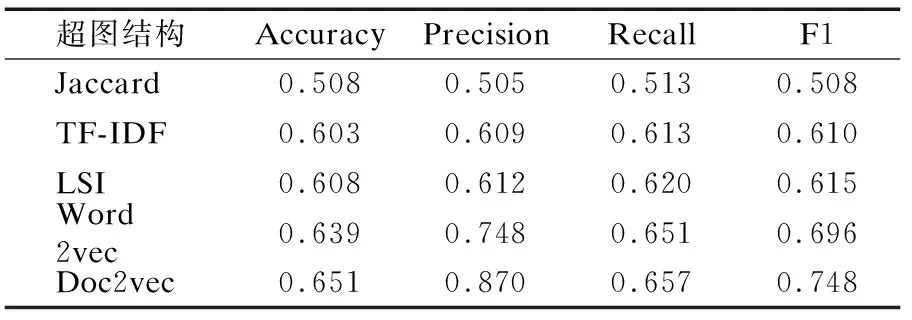
表3 异构超图结构分类实验-CtripTable 3 Heterogeneous hypergraph structure classification experiment-Ctrip
由表2可知,Cat&Dog数据集中RVGG对应的分类性能最高,说明基于RVGG提取的特征构造的超图结构质量最好,PHA对应的分类性能最低,说明基于PHA提取的特征构造的超图结构质量最差.由表3可知,Ctrip数据集中Doc2vec对应的分类性能最高,说明基于Doc2vec提取的特征构建的超图结构质量最好.Jaccard对应的分类性能最低,说明基于Jaccard处理方式得到的超图结构质量最差.表2和表3反映了不同特征提取方式对应的超图结构质量,对于图像数据集使用RVGG方法可得到高质量的超图结构,对于文本数据集使用Doc2vec方法可到高质量的超图结构,由于异构超图结构间的质量有差异,因此需要找到一个最优的方式去进行异构超图结构扩张,使得扩张后的超图结构质量高于单一超图结构.
4.3 超图结构扩张分类实验
表4所示为在文本和图像数据集上,不同超图结构扩张的组合对分类性能的影响.第1列表示选取的数据集,第2列表示不同的超图结构组合方式及名称,如“差+差PHA+SIFT”指将基于PHA和和SIFT特征提取方法构造的超图结构扩张为一个新的超图结构.根据表2的结果,这两种方法单独构造的超图质量最差,属于“差+差”组合方式.结合表2和表3,每类数据集的第2种扩张组合是一个质量最优和一个质量最差的超图结构,第3种扩张组合是两种质量最优的超图结构.表4中3~6列为每种扩张结构在4个指标上的结果.

表4 超图结构扩张组合分类实验结果Table 4 Experimental results of extended combinatorial classification of hypergraph structure
将表4扩张超图结构的分类结果与表2和表3单一超图结构分类结果可知,当两个超图结构质量相当的时候,使用异构超图结构扩张方法有利于提高分类性能.如Cat&Dog数据集上,根据表2,PHA和SIFT对应的超图结构质量最差,表4中超图扩张结构PHA+SIFT在4个分类指标上,要优于表2中的PHA和SIFT单超图结构.同样由表2可知RVGG和HVGG对应的超图结构质量最优,表4中RVGG+HVGG扩张结构在4个分类指标上都高于RVGG和HVGG单超图结构,说明扩张后的超图结构质量变高,因而得到了高质量的Laplacian矩阵.
当两个超图结构质量相差过大的时候,异构超图结构扩张反而不利于提高分类性能,如表4中,RVGG+PHA扩张结构中RVGG单一超图结构质量最优,PHA单一超图结构质量最差,RVGG+PHA对应的4个分类指标都低于RVGG,说明扩张后的超图结构质量低于RVGG单超图结构的质量.因此本文的超图结构扩张方法要选取质量相当的超图结构组合.为了得到最好的分类结果,应当将质量高的超图结构扩张为一个新的结构.
图4和图5反映了超图结构的扩展性,即超图结构扩张个数对分类效果的影响.图4和图5的横轴表示通道数,图下方对应了不同扩张个数得到的分类指标,4个分类指标的曲线反映了分类指标随着扩张数增加的变化趋势.根据表4,高质量的超图结构扩张能得到更好的效果,因此图4和图5实验选择高质量的超图结构扩张.其中Cat&Dog数据集的横轴1-4分别对应RVGG、RVGG+HVGG、RVGG+HVGG+VGG、RVGG+HVGG+VGG+Resnt这4种超图结构扩张组合.Ctrip-数据集的横轴1-4分别对应Doc2vec、Doc2vec+Word2vec、Doc2vec+Word2vec+LSI、Doc2vec+Word2vec+LSI+TF-IDF这4种超图结构扩张组合.根据图4和图5实验结果,通道数大于等于2之后,分类指标曲线基本趋于稳定,因此不需要扩张过多的超图结构.
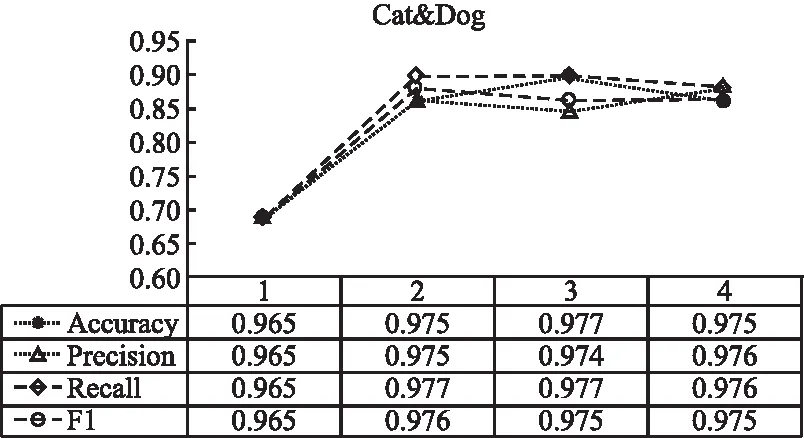
图4 Cat&Dog—扩展数影响Fig.4 Cat &Dog-influence of expansion number

图5 Ctrip—扩展数影响Fig.5 Ctrip-influence of expansion number
4.4 多通道超图Laplacian矩阵融合实验
表5所示为不同超图结构组合对多通道Laplacian矩阵融合方法的影响,单一超图结构则对应单通道.第1列表示选取的数据集,第2列表示不同通道Laplacian矩阵组合,如PHA+SIFT指首先得到PHA和SIFT对应的超图结构,之后计算两个超图结构对应的Laplacian矩阵,再加权累加.第3~6列表示每种组合方式在4个指标上的结果.结合表2和表3的结果可知,质量相当的超图结构对应的Laplacian矩阵融合有利于提升分类精度.如Ctrip数据集上,根据表3,Jaccard和TF-IDF对应的超图结构质量最差,表5多通道Laplacian矩阵融合Jaccard+TF-IDF分类指标高于表3中Jaccard和TF-IDF的单通道结果.Doc2vec和Word2vec对应的超图质量最优,则表5中Doc2vec+Word2vec矩阵融合后的分类指标同样高于表3中Doc2vec和Word2vec的单通道结果,说明融合后的Laplacian矩阵质量变高.然而当两个超图结构质量之间相差过大的时候,Laplacian矩阵融合后的效果反而会降低.表3中,Doc2vec对应的超图结构质量最优,TF-IDF对应的超图结构质量最差,表5中Doc2vec+TF-IDF矩阵融合后的4个分类指标低于表3中Doc2vec单通道结果.因此在使用本文提出的两个优化Laplacian矩阵方法之前,考察超图结构的质量是一个必要的步骤,将质量高且相差不大的超图结构对应的Laplacian矩阵融合能够得到最好的结果.

表5 Laplacian矩阵通道组合分类实验结果Table 5 Experimental results of Laplacian matrix channel combination classification
下面考虑多通道Laplacian矩阵融合方法的扩展性,即通道数对Laplacian矩阵融合效果的影响,如图6和图7所示.图中的横轴表示通道数,图下方的数据表反映了不同的通道数对应的分类指标,4条曲线反映分类指标随着通道数增加的变化趋势.根据前述表4和表5的实验结果都证明质量高且相差不大的超图结构组合,可以获取更高的分类性能,因此图6和图7实验选择高质量的超图结构实现多通道Laplacian矩阵融合.其中Cat&Dog数据集的横轴1-4分别对应RVGG、RVGG+HVGG、RVGG+HVGG+VGG、RVGG+HVGG+VGG+Resnet这4种通道组合.Ctrip-数据集的横轴1-4分别对应Doc2vec、Doc2vec+Word2vec、Doc2vec+Word2vec+LSI、Doc2vec+Word2vec+LSI+TF-IDF这4种通道组合.图6和图7的4个指标曲线增长趋势说明,通道数大于等于2之后,分类性能基本趋于稳定,多通道Laplacian矩阵融合不需要太多的计算通道.因此在表6的对比实验中两种优化方法都是基于两种最优的超图结构进行组合实验.
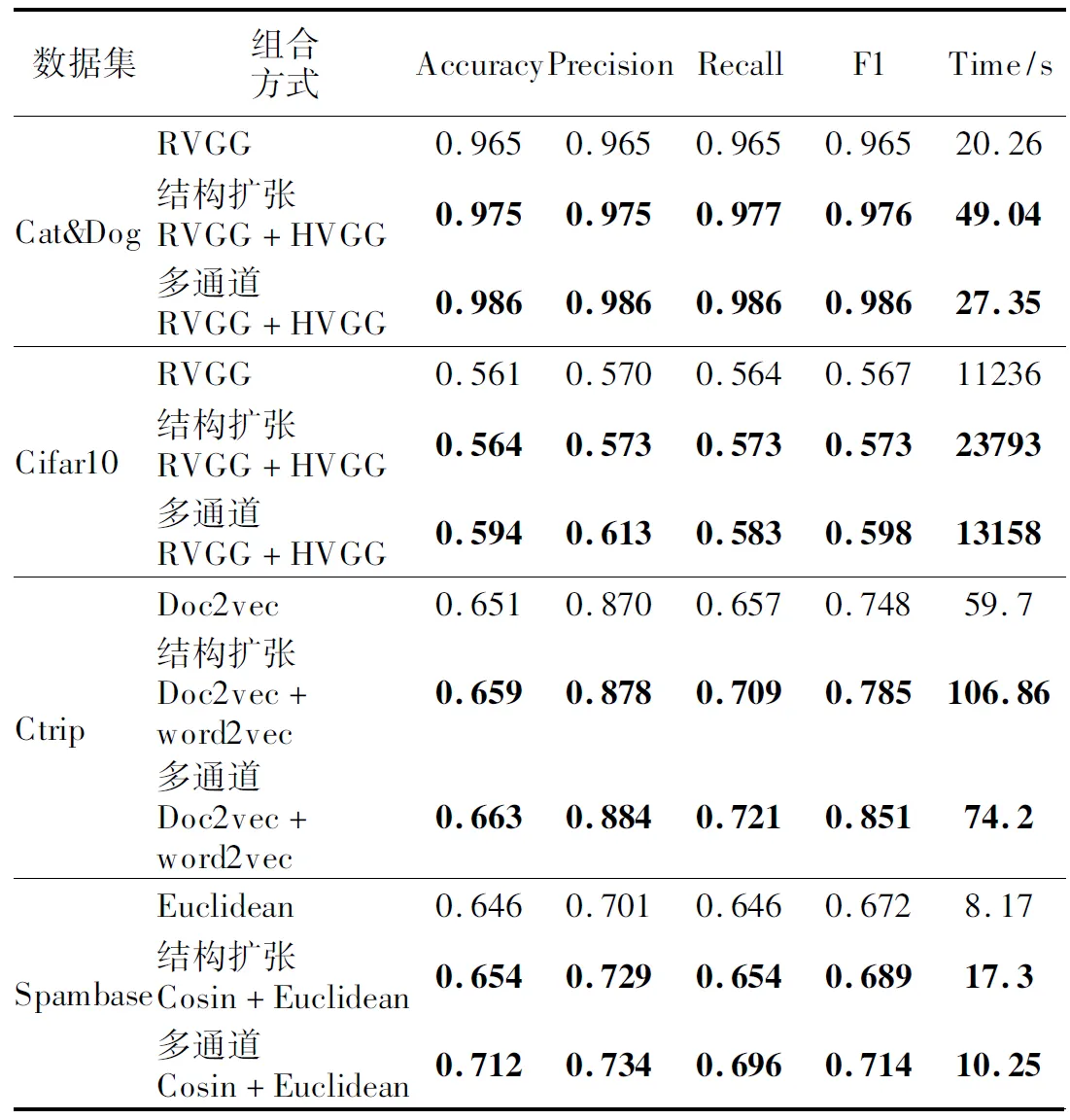
表6 两种优化方法对比实验Table 6 Comparative experiment of two optimization methods

图6 Cat&Dog-通道数影响Fig.6 Cat &Dog-influence of channel number

图7 Ctrip-通道数影响Fig.7 Ctrip-influence of channel number
上述实验在部分数据集上探究本文两种方法的适用场景,表6在4个数据集上对比两种方法的分类性能,第1列表示4个数据集,第2列表示组合方式,第3~6列表示4个分类的值,最后一列是不同组合方式的时间开销.每个数据集对应的第1行表示这个数据集上最优单一超图结构的分类结果.第2行表示超图结构扩张法,拼接两个质量最优的超图结构,超图结构质量可参考表2和表3的实验结果.第3行表示多通道Laplacian矩阵融合法,融合两个质量最优的超图结构对应的Laplacian矩阵.由于Spmbase数据集是数值型数据不涉及特征提取操作,本文分别使用欧式距离和余弦距离计算样本间相似度得到两种不同的超图结构,之后基于这两个超图结构分别使用超图结构扩张法和多通道Laplacian矩阵融合法,与单超图结构的分类性能做对比.表6对比的实验结果证明异构超图结构扩张法有利于提高超图模型对样本分类的效果,而多通道Laplacian矩阵融合法相比超图结构扩张法可进一步提高模型分类的效果,如Spambase数据集,单个超图结构对应的4个分类指标分别为0.646、0.701、0.646、0.672,超图结构扩张法对应的4个分类指标分别为0.654、0.729、0.654、0.689,多通道Laplacian矩阵融合法对应的4个分类指标分别为0.712、0.734、0.696、0.714.此外由表6中Time列的实验结果可知,多通道Laplacian矩阵融合法相对异构超图结构扩张法可降低大量的时间开销,4个数据集上可分别降低44.2%、44.6%、30.3%和40.7%的时间成本,平均降低40%左右.
4.5 多通道超图Laplacian矩阵加权融合实验
4.4节超图Laplacian矩阵融合实验基于的假设是,每个Laplacian矩阵的贡献是相同的,因为它们具有相同的系数.然而每个Laplacian矩阵所描述的视图不同,因而应该讨论不同通道Laplacian矩阵的重要程度,4.5小节实验通过设置不同的权重参数来衡量不同通道Laplacian矩阵的重要性.根据表5和表6的实验结果,多通道Laplacian矩阵融合相比超图结构扩张有更好的分类效果,且时间成本更低.由图6和图7可知Laplacian矩阵融合在两个通道后分类效果基本趋于稳定,因此4.5小节讨论两种质量最高的加权通道融合结果.对于Cat&Dog数据集选择RVGG+HVGG通道加权融合,Ctrip选择Doc2vec+word2vec通道加权融合.
即公式(9)Laplacian矩阵的计算变为L=a1×L1+a2×L2,其中L1和L2分别对应两个通道的Laplacian矩阵,a1和a2分别表示两个Laplacian矩阵的权重.由于a1、a2是非凸优化的,在更新F和超边权重矩阵W之后,使用Tree-structured Parzen Estimator(TPE)算法求解a1和a2.如图8所示,Orginal loss表示a1,a2=1的损失值,由于此时的损失值是F和W优化之后的损失,因此是个定值.TPE loss表示使用TPE算法搜索参数a1,a2后的损失变化,根据实验结果可以发现,TPE算法迭代100次的损失最小值基本趋于为稳定,有效的降低了损失值.最终的参数取值对应TPE loss曲线的最低点.

图8 TPE算法-优化参数Fig.8 TPE algorithm-optimizing parameters
4.6 与经典分类模型性能对比
4.6节主要使用了4.4节的实验结果与其它一些经典机器学习模型分类效果的对比,对比的分类模型包括经典的KNN、SVM、SVM+进化算法、图直推学习模型[34]、超图直推学习-CD、超图直推学习-GD,超图直推学习-Feng.SVM+进化算法指得是使用进化算法来搜寻SVM的变量取值.超图直推学习-CD指得是使用坐标下降的方式来解决超图分类问题,对应公式(13)和公式(14).超图直推学习-GD指得是使用交替最小二乘法来解决超图分类问题,对应公式(11)和公式(12).超图直推学习-Feng指得是Feng提出的关联矩阵优化的方式[16].在两个不同类型数据集上进行实验,对于文本数据集(Ctrip)和图像数据集(Cat&Dog)首先使用Word2vec特征处理方式和RVGG的方式提取特征,输入前6种不同的机器学习分类模型进行分类,之后对比两种优化超图直推学习模型的实验结果.
如图9和图10,本文提出的两种优化超图直推学习模型的方法,超过了经典的SVM算法及其改进算法,由于普通图表达的顶点间关系不如超图丰富,因此普通图直推学习模型的效果不如超图直推学习模型.而且本文提出的优化方法分类性能高于超图直推学习-CD和超图直推学习-GD两种直推学习模型的优化方法,是由于改进后的超图扩张结构以及多通道Laplacian融合矩阵,相比原来单一的超图结构表达了更多的顶点间、顶点超边间的复杂关系信息.超图直推学习-Feng忽略了超边权重的信息,因此效果也不如本文提出的两种优化方法.
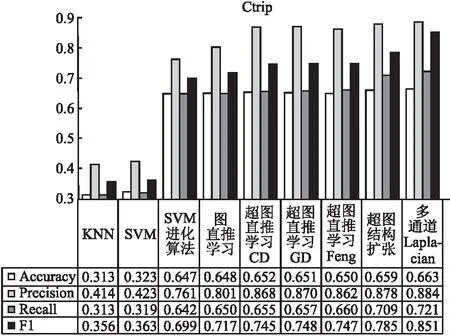
图9 Ctrip数据集分类结果对比Fig.9 Comparison of classification results of Ctrip data set
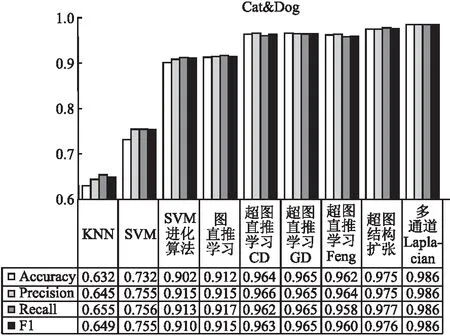
图10 Cat &Dog数据集分类结果对比Fig.10 Comparison of Cat &Dog dataset classification results
5 结 论
本文针对超图直推学习模型的求解和优化问题,采用了两种方法.首先提出了超图结构扩张法,将超图关联矩阵拼接.同时引入权重信息,将不同关联矩阵对应的权重矩阵也进行拼接,以增加Markov随机游走的扩散范围.实验结果表明这种方式可以有效提高超图直推学习模型的分类性能,但矩阵拼接也带来了矩阵维度高,时间开销大的问题.因此本文进一步提出了多通道Laplacian矩阵融法,在多种特征提取方式构造的异构关联矩阵的基础上,将多个计算通道得到的Laplacian矩阵加权求和,再进行超图分割,不仅降低了时间开销,且进一步提高了模型的分类性能.最后通过与SVM等经典模型以一些改进的超图直推学习模型进行比较,验证了本文提出的两种方法的效果.现阶段随着超图神经网络的提出,超图在深度学习领域逐渐显示出了其高效的性能,因此未来研究的重点将放在超图深度学习模型及其优化方面.

