110 kV单芯电缆缆芯暂态温度径向感知模型研究

王伟平，周 恒，梁国坚，张 琛，张志方

（1.广东电网有限责任公司中山供电局，广东中山 528400；2.武汉大学电气与自动化学院，湖北武汉 430072）

0 引言

高压电缆作为电力系统中的关键电力设备，需要对其动态载流能力开展研究，热点温度是影响电缆载流量的关键参量[1-2]。缆芯温度的实时监测对于电缆安全运行、动态载流能力调度具有重要意义。

国内外对电缆缆芯温度的估算方法可分为4类，分别为温升试验法[3-5]、数值计算方法[6]、解析计算方法[7]、侵入及非侵入式在线测温法[8-9]。温升试验方法是最直接的获取缆芯温升的方法，但是试验法成本高，试验线路难以模拟实际线路复杂多变的运行环境。解析计算方法源自于热路模型，以IEC60853 标准为主，该方法建立在一系列假设的基础上，长期被各地电力部门使用，但计算结果偏于保守，不能有效指导电缆安全运行及动态载荷能力调度需求[10]。数值计算可以模拟任意的环境条件，可以给出较为准确的计算结果，但数值法计算耗时较长，难以获取实时测量结果[11-13]。侵入式测温通常在内部预先铺设了测温光纤的电缆测温，可以对电缆缆芯的温度开展连续、实时测量，但是其成本高，内置光纤的损坏甚至会引起电缆本体绝缘故障且不适用于大量在运设备。非侵入式测温通常是在电缆表面放置传感器，在准确获取表面温度的基础上，建立缆芯温度径向感知热路模型反演电缆的缆芯温升。非侵入式的缆芯热点温度辨识是近年来研究较多的一种方法[14-16]。

热路法在构建电缆内外区域热路模型时往往要求电缆周围的介质为单一均匀的介质，而电缆线路距离长，敷设环境复杂，采用单一的环境参数存在误差[17]。针对于散热环境介质不均匀、散热条件不一的问题，阮江军等学者提出了基于电缆表皮温度测量的电缆接头温度反演方法[18]，该研究通过设计测温点阻滞层，消除了外界环境的影响，此时模型计算的焦点集中于电缆缆芯温度径向感知模型的构建和热参数的选取。如何提高缆芯温度径向感知模型的计算精度成为主要研究点，集中参数建模方法目前得到广泛认可。文献[19-20]认为，采用集中参数建模存在误差，主要原因是绝缘层导热性能不佳，靠近缆芯侧与绝缘层外侧温差较大，以内侧绝缘层的温度代替整个绝缘层的温度会使其热容偏大。文献[16]提出将绝缘层分成若干层，提出了按照一定的比例分配绝缘层的热参数。在此基础上，刘刚、王鹏宇等对绝缘层进行分层建模分析，研究表明分层到一定程度后对求解精度影响不大，但是会增加求解时间，给出了15 层的分层建议[20]。是否存在一个最合适的分层数使热路模型计算精度达到最佳，并验证分析，需要进一步研究。

为了进一步提高电缆本体内部温度辨识的精度，本文提出了一种110 kV 单芯电缆缆芯温度的径向感知模型。首先建立电缆各层结构的热阻热容集中参数等效模型，对径向感知模型的误差来源进行了分析，并讨论了热路模型中电缆交联聚乙烯层分层处理的必要性及处理方法。其次结合110 kV单芯电缆本体温度场仿真计算模型，分析了交联聚乙烯绝缘建模（Cross Linked Polyethylene，XLPE）的分层数量和分层方式。最后针对材料参数的分散性对反演精度的影响开展研究，为电缆缆芯温度的准确计算奠定基础。

1 电缆本体热力学特征分析

1.1 基本结构参数

本文研究的电缆为110 kV 交联聚乙烯皱纹铝护套聚乙烯纵向阻水电力电缆，具体型号为YJLW03-Z 64/110 kV 630 mm2。电缆剖面结构如图1 所示，从内到外依次由缆芯、内屏蔽层、XLPE 层、外屏蔽层、半导电阻水带、皱纹铝护套和外护套组成。表1 给出了本文各结构具体的尺寸参数与各结构采用的热力学参数。

表1 电缆缆芯各层几何及热力学参数Table 1 Geometrical and thermodynamic parameters at each layer of cable core

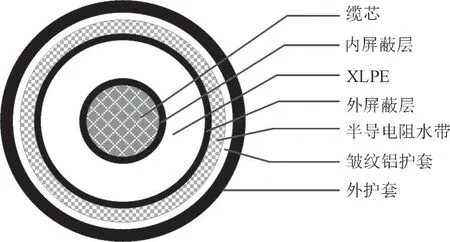
图1 缆芯剖面结构Fig.1 Structure of cable core section

同时，为分析单芯电缆材料特性影响，通过文献调研确立了各层材料导热系数的取值范围。具体包括：1）缆芯对应紫铜的导热系数取值范围为[383[21]，401[22]]；2）XLPE 的导热系数取值范围为[0.25[23]，0.46[24]]；3）半导电阻水带导热系数取值范围为[0.15[25]，0.6[21]]；4）聚乙烯导热系数取值范围为[0.23[26]，0.5[21]]。

1.2 温度场分布规律分析

首先进行有限元（Finite Element Method，FEM）温度场瞬态仿真计算。电缆本体的温度场为二维平面场，参照电缆几何结构参数和热力学参数建模，从内到外依次为缆芯、绝缘层、阻水带、铝护套及外护套。网格划分采用自由剖分，由于模型较小，一共产生24 090 个单元，12 146 个节点。

按照表1 进行建模，设置材料参数及对应激励，仿真中对瞬态温度场进行计算。假设初始时刻整个电缆的温度均匀分布为25 ℃，电缆中依次通入1 000 A，800 A，600 A，1 200 A，700 A 的电流，加载时间间隔为1 h，总共5 h，环境温度设置为25 ℃。最终得到了各时刻下不同结构的温度变化如图2所示，可以看出，缆芯外侧结构温度沿径向迅速降低，并接近于运行环境温度。

图2 电缆各层温度随时间变化曲线Fig.2 Temperature variation curves with time at each layer of cable

进一步分析了5 h 末缆芯温度梯度分布云图，并提取径向温度梯度曲线如图3 所示。可以看出，径向位置对应的结构中，XLPE 的温度梯度较大，且越靠近缆芯，温度梯度变化越大。因此XLPE 需要采用多层细分，且从内到外分层厚度依次增加。

图3 5 h末径向温度梯度变化曲线Fig.3 Radial temperature gradient change curve at the end of five hours

2 径向感知模型的建立与求解

2.1 径向热路分布参数模型与误差分析

高压电缆的截面直径往往远小于其长度，且结构呈平面对称分布，因此分析电缆的传热过程时，忽略其轴向传热而只考虑径向的温度梯度。在电缆径向切面半径r处取1 单位长度的圆筒微元如图4 所示。

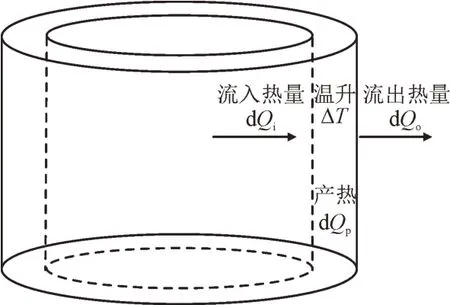
图4 微元圆筒壁热平衡分析Fig.4 Heat balance analysis of micro-element cylindrical wall

在时间dt内流入该微元圆筒壁的热量为dQi，流出微元圆筒壁的热量为dQo，微元圆筒壁产热dQp。设微元圆筒壁体积dV，微元圆筒壁比热容为c，密度为ρ，则根据能量守恒定律，可得该微元圆筒壁在时间dt内的温升为ΔT，令dQi/dt=Pi，dQp/dt=Pp，则有：

式中：Pp为电缆导体产热率；Pi为热流率；λ为热导率。

微圆筒微元的暂态热路分布参数模型如图5所示，为Γ型等效热路。其中，2πrλ∂T/∂r为注入热容的热功率Pi，2πrcρdrΔT/dt为储存在微元热容的热量Pp。以上分析均是基于严格的数学推导，因此圆筒微元的暂态分布参数模型是准确的。

图5 微元圆筒壁微元热路模型Fig.5 Thermal circuit model of micro-element cylindrical wall

将圆筒微元扩展为半径r1至r2之间的圆筒（r1＜r2），并设r1处的温度为T1，r2处的温度为T2，则流经热阻的热功率PR和注入热容的热功率PC经积分为：

式（3）中引入了集中参数近似处理的第一个误差来源，即只有当ΔT不随r变化时，式（3）才严格成立。而事实上ΔT是半径r的函数，因此采用集中热容等效时要求该处温度梯度足够小，若温度梯度太大，则必须将其分为多个集中元件，从而减小误差。基于上述假设的热阻R和热容C表达式简化为：

通过式（4）—式（5）可求得电缆各层的热阻和热容如表2 所示，其中缆芯和铝护套材料的热导率非常高，热阻很小，可以将其忽略，从而减小计算量。

表2 电缆各层热容和热阻Table 2 Thermal capacity and thermal resistance at each layer of cable

热路模型的第二个误差来源在于集中参数和分布参数难以完全等效，只有在一定条件下才可忽略这一误差。仿照电路对热路模型进行分析，热量从一端到另一端的时间可以用时间常数描述。

式中：τi为第i层圆筒的时间常数，Ri和Ci分别为第i层圆筒的热阻和热容。

计算可得电缆各层时间常数如表3 所示。可知，XLPE 的时间常数超过半个小时，半导电阻水带的时间常数均不到1.5 min，而负荷波动的周期往往在10 min 以上。综上，半导电阻水带和外护套可以采用集中参数处理，而XLPE 层必须要进行细分，以减小集中参数带来的误差。

表3 电缆各层的时间常数Table 3 Time constant at each layer of cable s

2.2 径向感知模型的建立

2.1 节研究了微元圆筒壁微元热路模型，分析了热平衡，热阻、热容参数的获取方法等。由于电场和热场的高度相似性，电流对应热流，电压对应温差，电阻电容近似热阻、热容。电缆导体施加电流，以导体为中心热量向轴向和径向传导，缆芯的传热可以由电缆本体热损及周围介质等效的热阻和热容串并联来描述。

由于可在外护套表面布置温度传感器，因此外护套表面的温度Tn-1的温度是已知的。根据电路理论中的替代定理：在一个具有唯一解的任意电路中，若已知某支路k（k=1，2……）的电压uk、电流ik，并且该支路与电路中的其他支路不存在耦合作用，则无论该支路由什么元件构成，都可以用一个大小和极性均与原支路电压uk相同的电压源或电流大小和流向与原支路电流ik相同的独立电流源来替代。故可以用一个热压源来替代环境部分热路的影响。

径向感知模型最终等效为若干热阻和热容的联结，等效时忽略缆芯和铝护套的热阻，仅考虑热容。近似处理后的电缆本体暂态径向感知热路模型如图6 所示。C0和T0分别表示缆芯的热容和外表面温度。C1-Cn-3和R1-Rn-3分别表示XLPE 及内外屏蔽层各层的热容和热阻，T1-Tn-3表示XLPE 及内外屏蔽层各层的外侧温度。Cn-2，Rn-2和Tn-2分别表示阻水带的热容、热阻和外表面温度。Cn-1表示铝护套的热容，Cn，Rn-1和Tn-1分别表示外护套的热容、热阻和外表面温度，Ts为传感器测量的外护套表面温度，Ps为单位长度缆芯的焦耳热，可用电流I，电阻率ρ和横截面积S表示,即Ps=I2R=I2ρ/S，是热路模型中唯一的热源。本文暂时不考虑介损和环流的影响。

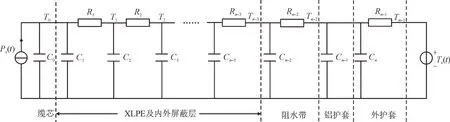
图6 改进的电缆暂态热路模型Fig.6 Improved transient thermal circuit model of cable

2.3 径向感知模型的求解

先不对XLPE 进行分层，对其求解结果进行分析。首先列写对应暂态热路模型状态变量方程，根据基尔霍夫定律列写如式（7）所示：

将式（7）进行处理，可得暂态热路模型的状态方程如式（8）所示。

具体求解中，可以将方程写为状态方程的一般形式：

式中：X为n维状态变量向量，X=[x1（t）x2（t）…xn（t）]T；在热路模型中对应各个节点温度；为X对时间导数；A和B均为实常系数矩阵；U为输入列向量；X（0-）为初值。

对式（10）进行拉普拉斯变换可得：

整理可得：

对式（12）进行拉普拉斯逆变换即可得到状态变量的时域表达式。

图6 中径向感知模型中的热阻、热容参数由表2给定，且有Ts（t）=T3=25℃，Ps（n）=I（n）2ρ/（πr12），其中铜的电阻率ρ为1.75×10-8Ω·m，缆芯半径r1=15 mm。可得Ps（1）=24.75 W，Ps（2）=15.84 W，Ps（3）=8.91 W，Ps（4）=35.65 W，Ps（5）=12.13 W，最终构建图7 所示的径向感知热路模型。

图7 外护套表面温度恒定、XLPE不分层时热路模型参数Fig.7 Thermal circuit model parameters with constant temperature of outer sheath surface and XLPE insulation without layering

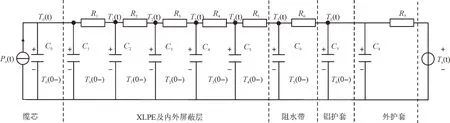
图8 XLPE分5层时的暂态热路模型Fig.8 Transient thermal circuit model of XLPE insulation with five layers

为对比分析，按照从内外到厚度逐渐增加的方式对XLPE 进行细分，一共分为5 层，每层的外半径依次为17.67 mm，20.81 mm，24.51 mm，28.87 mm 和34 mm。按照式（4）和式（5）可分别求得XLPE 每层的热阻热容参数如表4 所示。

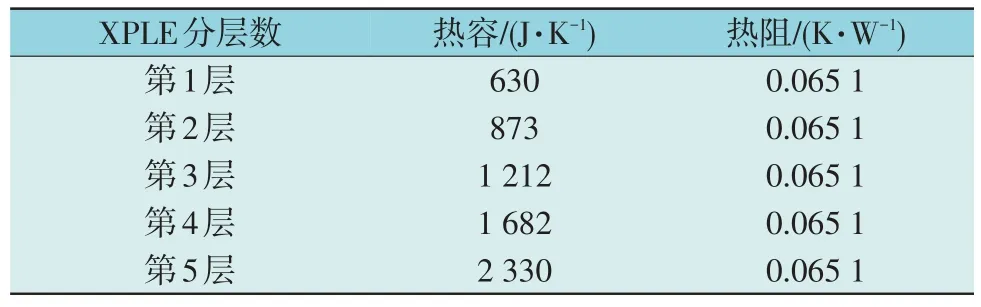
表4 XLPE各层热容和热阻Table 4 Thermal capacity and thermal resistance at each XLPE insulation layer

3 径向感知模型温度反演验证

3.1 分层数对求解精度影响分析

对图7 电缆缆芯热路模型进行求解获得了不同位置温度瞬态变化曲线，并与有限元仿真计算的结果进行对比，结果如图9（a）所示。可以看出，XLPE不分层建模时的径向感知求解模型，对缆芯温度的估算结果误差较大，整体计算值偏小。尤其是温度变化后期，缆芯外侧温度最大相对误差约16.21%。

图9 XLPE是否分层的温度反演值与有限元仿真结果对比Fig.9 Comparison of temperature inversion values and FEM results between XLPE insulations with and without layering

同样将采用XLPE 分层时建立的径向感知暂态热路模型求解结果与有限元仿真计算结果进行对比，电缆各层温度对比如图9（b）所示。可见，此时精度较之前XPLE 不分层时大大提高，各层内外侧有限元仿真结果与反演值基本重合，也验证了前面理论分析的正确性。

3.2 外护套等效效果分析

为验证将外护套设置为恒定热压源是否合适，将电缆放置在空气中，并令其表面对流换热系数尽可能小，取为2 W/（m2·K），让外护套表面温度变化较为明显。同样地，假设初始时刻整个电缆的温度均匀分布为25 ℃，电缆中依次通入大小为1 000 A，800 A，600 A，1 200 A，700 A 的电流，加载时间间隔为1 h，总共5 h。提取外护套温度作为温度反演的边界条件，即热压源，采用径向感知模型进行温度反演，得到电缆各层温升随时间变化曲线如图10 所示。可见各层反演误差很小，效果良好，证明了可以将外护套用热压源来替代环境部分热路的影响。

图10 边界温度波动时反演值与有限元仿真结果对比Fig.10 Comparison of inversion values and FEM results with boundary temperature fluctuation

3.3 电缆参数的敏感性分析

实际电缆各结构的参数均有一定的分散性，因此需要分析材料参数对径向感知模型精度的影响。考虑实际应用过程中各个因素都可能发生变化，为充分分析多种本体材料组合的影响情况，以1.1 节的各结构导热系数的取值范围中的最小值和最大值作为基准，采用正交表的方式进行对比分析，共得到8 种组合。本体材料的正交组合表如表5 中编号1—8 所示。

表5 本体热导率正交组合表Table 5 Orthogonal combination table for thermal conductivity of cable body W·（m·K）-1

求解工况仍假设初始时刻整个电缆的温度均匀分布为25 ℃，电缆中依次通入大小为1 000 A，800 A，600 A，1 200 A，700 A 的电流，加载时间间隔为1 h，总共5 h。本文选取编号为1，3，5，7 的组合进行温度场有限元仿真分析，以仿真得到的缆芯各个时刻的温度变化曲线与径向感知模型反演结果进行对比，其结果如图11 所示。可以看出，相较于编号1，编号3 由于交联聚乙烯和半导电阻水带的导热系数增加，传热性能增强，缆芯温度低于编号1。编号5 相较于编号1 由于半导电阻水带影响，缆芯温度降低。但本文建立的模型仍可以准确地反演材料参数改变后的缆芯温度，说明该反演算法能够较好地克服电缆材料参数的分散性。

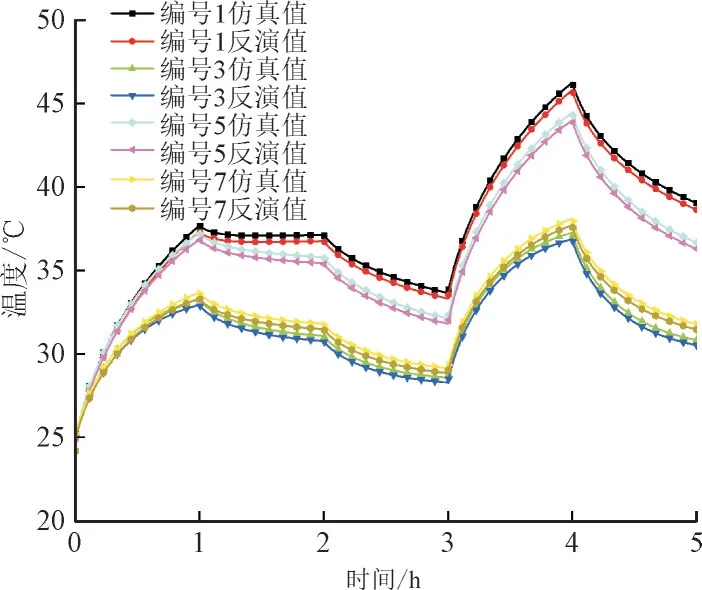
图11 XLPE分5层时的温度反演值与有限元仿真结果对比Fig.11 Comparison of temperature inversion values and FEM results of XLPE insulation with five layers

4 结论

本文以110 kV 单芯电缆为研究对象，对缆芯温度径向感知热路模型开展研究，确定合理分层数并进行暂态温升反演计算，并与有限元仿真计算值进行对比验证，具体结论如下：

1）电缆缆芯绝缘层的温度梯度结果表明，越靠近缆芯，温度变化越大，因此绝缘层需要采用多层细分，且从内到外分层厚度依次增加的方式。

2）XLPE 分层且细分时，各层温度反演结果与有限元仿真计算结果基本一致，合理分层数为5 层。

3）暂态径向感知热路模型能够准确地反演材料参数改变后的缆芯温度，说明模型能够较好地克服缆芯材料参数分散性。