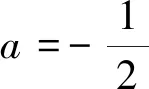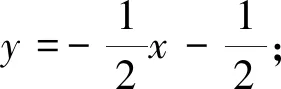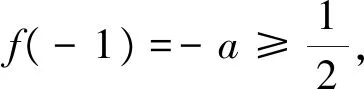高等数学观点下寻根探源必要性的入手“点”*

李加军

北京市第一0一中学怀柔分校 (101407)

初等数学的有些问题需要在高等数学的理论里加以解释.数学家克莱因指出:“有许多初等数学的现象只有在非初等的理论结构内,才能深刻地理解.基础数学教师,应该站在更高的视角(高等数学)来审视、理解初等数学问题,只有观点高了事务才显得明了而简单.”[1]因此,高中数学教师许多时候要善于在高等数学的观点指导下研读教材、研习习题,从而整体上深度把握数学思想,只有进整体思考,问题才看得清,说得明.比如与函数导数相关的数学内容与问题,我们可以适当联系高等数学里的中值定理、泰勒展开、洛必达法则求极限等等.下面我将结合一些具体实例阐明高等数学中的费尔马(Fermat)定理对寻求不等式恒成立的必要性入手“点”的指导作用.

1.费尔马(Fermat)定理

若(1)函数f(x)在点x0的邻域(x0-δ,x0+δ)(δ>0)内有定义,并且在此邻域内恒有f(x)≤f(x0)或者f(x)≥f(x0);(2)函数f(x)在x0点可导,则有f′(x0)=0.

推论1 若(1)函数f(x)在点x0的邻域(x0,x0+δ)(δ>0)内有定义,并且在此邻域内恒有f(x)≤f(x0)(f(x)≥f(x0));

2.实例分析

例1 (北京市海淀区2022届期末考试题)函数f(x)=aex-sinx+2x.(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方程;(Ⅱ)当a≥0时,求函数f(x)在[0,1]上的最小值;(Ⅲ)直接写出a的一个值,使f(x)≤a恒成立,并证明.

解析：试题前两问非常常规,易得答案分别为(Ⅰ)y=(a+1)x+a;(Ⅱ)a.第(Ⅲ)问详细解答如下:

取a=-1,下面证明-ex-sinx+2x≤-1恒成立,即证ex+sinx-2x-1≥0恒成立,令g(x)=ex+sinx-2x-1,即证g(x)≥0恒成立,求导g′(x)=ex+cosx-2.

(i)当x≤0时,ex≤1,cosx∈[-1,1],此时g′(x)≤0,所以函数g(x)在(-∞,0]上单调递减,∴g(x)≥g(0)=0,即g(x)≥0成立;

(ii)当x>0时,令p(x)=g′(x)=ex+cosx-2,x>0,p′(x)=ex-sinx,因为ex>1,sinx∈[-1,1],所以p′(x)>0,所以函数g′(x)在(0,+∞)上单调递增,∴g′(x)>g′(0)=0,所以函数g(x)在(0,+∞)上单调递增,∴g(x)>g(0)=0.

综上可知,g(x)≥0恒成立,即f(x)≤a恒成立.

点评：到目前为止,问题仿佛一切皆顺利解决,但是学生会提出疑惑:为什么选a=-1?a的值还有没有其它选择?这就需要我们借助费尔马定理给出合理解释:因为f(x)≤a可以转化为h(x)=aex-sinx+2x-a≤0=h(0),h(x)满足费尔马定理在点0处的条件,所以h′(0)=0,于是可知a=-1是唯一满足的必要条件,此时知道入手“点”是“h′(0)=0”．从而上述解答顺理成章.如此一来,学生有了解答问题的明确依据,不再是猜或者蒙,轻而易举突破试题解答难点.

解析：(Ⅰ)(Ⅱ)问解答从略.

x(0,x0)x0(x0,1)F′(x)-0+F(x)↘极小值↗

综上所述可知,k的最大值为2．

点评：本题第(Ⅲ)问求k的最大值.如果学生能敏锐地观察到第二问中k=2时结论成立,就可以快速想到问题的方向是说明当k>2时,结论不成立,从而减少讨论,直接指向解题目标,从而快速有效地解决问题,对提升学生的逻辑推理能力大有裨益．

例3 (北京市海淀区2023届期中考试题) 已知函数f(x)=ex-asinx．(Ⅰ)当a=2时,求曲线y=f(x)在点(0,f(0))处的切线方程;(Ⅱ)当a=1时,证明:函数y=f(x)-2区间(0,π)上有且仅有一个零点;(Ⅲ)若对任意x∈[0,π],不等式f(x)≥2-cosx恒成立,求a的取值范围．

解析：(Ⅰ)(Ⅱ)问解答从略.

(Ⅲ)令h(x)=f(x)-2+cosx=ex-asinx+cosx-2,则问题转化为对任意x∈[0,π],h(x)≥0恒成立;又h′(x)=ex-acosx-sinx,令t(x)=h′(x),则t′(x)=ex+asinx-cosx;当a≥0时,若x∈[0,π],则ex≥e0=1,cosx≤1,sinx≥0,∴t′(x)≥0在[0,π]上恒成立,则h′(x)在[0,π]上单调递增.

①当a>1时,h′(0)=1-a<0,h′(π)=eπ+a>0,∴∃x0∈(0,π),使得h′(x0)=0,且当x∈(0,x0)时,h′(x)<0,∴h(x)在(0,x0)上单调递减,此时h(x)

②当a=1时,h(x)=ex-sinx+cosx-2.当x∈(0,π)时,h′(x)>h′(0)=0,则h(x)在[0,π]上单调递增,∴h(x)≥h(0)=0恒成立,满足题意.

③当a<1时,h(x)=ex-asinx+cosx-2>ex-sinx+cosx-2,由②知,对任意x∈[0,π],h(x)>ex-sinx+cosx-2≥0,满足题意.

综上所述,实数a的取值范围为(-∞,1]．

点评：本例同例1一样问题是学生如何想到的临界值1呢?问题解决如下,令h(x)=f(x)-2+cosx=ex-asinx+cosx-2,则问题转化为对任意x∈[0,π],h(x)≥0恒成立;进而将问题转化为h(x)≥0=h(0)对[0,π]恒成立,于是根据费尔马定理推论1可知h′(0)=e0-acos0-sin0≥0,于是求得必要条件a≤1,入手“点”是“h′(0)≥0”．这样我们就可以先给出a=1时成立的证明,进而再证明a>1时结论不成立及a<1时结论成立,从而使得问题顺利解决．

例4 (北京朝阳区2021—2022第一学期高三期中试题)已知函数f(x)=tanx-kx3-x,k∈R.

解析：(Ⅰ)答案为y=0,解答从略.

数学核心素养的落实旨在让学生经历数学学习活动后,真正成为“数学人”,其特征包括“心中有数”(数学抽象)、“脑中有形”(直观想象)、“手中有法”(数学建模与数据分析)、“脚下有路”(逻辑推理与数学运算).在核心素养引领下站在高观点下解决数学问题,犹如赏析美妙的乐章．

授之以鱼,不如授之以渔.如果我们立足基础知识,理解数学基本思想,注重通法通用,深刻领悟数学核心素养,那么问题的解决甘之如饴,回味久长．