例析利用基底法解立体几何问题
刘 海
江苏省曲塘高级中学 (226661)
在2019人教A版必修第二册中,向读者介绍了利用立体几何研究现实世界中物体的形状、大小与位置关系;在选择性必修第一册中,又介绍了利用空间向量表示空间中的点、线、面等基本元素,通过空间向量运算解决立体几何问题.由此可见,对于立体几何问题,空间向量是一个非常好的工具.在近些年的高考解答题中,立体几何题往往就是建立空间直角坐标系,利用空间向量的坐标运算解决线线、线面以及二面角等问题.但是,不少题目的建系方案并不明显,亦或很难看出存在三组两两垂直的直线,那么此时如何不建立空间直角坐标系来解决问题呢?本文就此探讨如何利用空间向量的基底解决立体几何问题.
例题(2022年苏州高三第一学期期末)如图1,在四面体ABCD中,已知△ABD是边长为2的等边三角形,△BCD是以点C为直角顶点的等腰直角三角形,E为线段AB的中点,G为线段BD的中点,F为线段BD上的点.

图1
(1)若AG∥平面CEF,求线段CF的长;
(2)若二面角A-BD-C的大小为30°,求CE与平面ABD所成角的大小.

评注:此问直接利用综合法,结合线面平行的性质定理、中位线定理及解三角形中的余弦定理便可解决,属于简单题.
(2)第(2)问有一定的难度,一般可利用综合法或者建立空间直角坐标系后用空间向量的坐标运算来解决.


图2
评注:此方法对空间想象能力有较高的要求,探求CE与平面ABD所成角的平面角是解题的关键,许多学生都未能正确找到这个平面角.

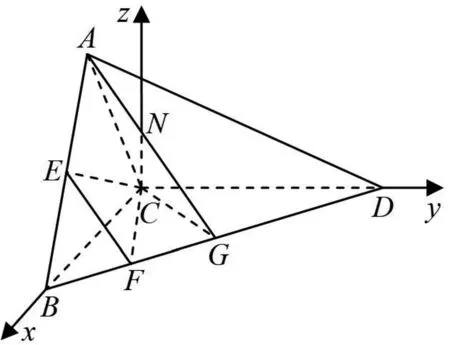
图3

评注:此方法中存在的难点是,①建系时z轴的确定;②求A点的坐标.
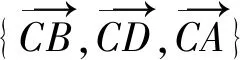
评注:此方法与方法二的最大区别在于,不需要找出或者构造三个互相垂直的向量来建立空间直角坐标系,只需要确定此空间里三个不共线的已知向量作为基底,从而大大减轻了没有直角依托情况下的求角求距离等立体几何问题.
其实,借助三个互相垂直的向量来建立空间直角坐标系是方案三中基底法的一种特例,即三个基底向量互相垂直.这也正是在平面向量中借助两个垂直向量来建立平面直角坐标系是利用平面中任一组基底解决问题的一种特例.
掌握好向量的基底法,可以有效解决因为题目中没有直角或不方便建系进而利用向量坐标运算来求解的问题.

