图运算下的基尔霍夫指数

邢抱花，孙旻昊

（安庆师范大学数理学院，安徽安庆 246133）

设G=(V(G),E(G))是无向的连通图，|V(G)|和|E(G)|分别表示G的顶点数和边数，d G(v)表示图G中顶点v的度，G-w表示在图G中删去顶点w以及与w关联的边后得到的图。若图G-w不再连通，则称顶点w是图G的割点，图G的不含割点的极大连通子图称为G的块，图G的两顶点u、v的距离d G(u,v)是指图G中连接u、v的最短路长度。将图G的每条边用单位电阻代替后，得到对应的电网络，图G中任意两点u和v的电阻距离ΩG(u,v)是对应电网络中的有效电阻。[1]电阻距离不同于一般的距离仅仅代表着两个顶点之间的最短路长度，它更能刻画整个图各顶点的关系，更适合描述分子中的流体和波状通信。自1993年，Klein和Randic首次提出电阻距离概念之后，关于它的相关结论被陆续发表，其中一部分研究内容是有关基于电阻距离的拓扑不变量，最常见的是基尔霍夫指数[2]，是1994年Bonchev和Balaban等人提出的，被定义为图G中所有无序顶点对的电阻距离总和。即

2007年和2012年，陈海燕等人和Gutman等人又分别定义了度积基尔霍夫指数[3]与度和基尔霍夫指数[4]

关于它们的部分结论可参看文献[2-18]及其参考文献。

近年来，有关基尔霍夫指数计算的结论主要分两方面：一方面是某些特殊图自身的基尔霍夫指数计算，如正则图[5]、硅酸盐网络[6]、脂环烃衍生物网络[7]等；另一方面是经过图运算后的图的基尔霍夫指数计算，如在文献[8]和[9]中，杨玉军等人计算了剖分图S(G)、叠代剖分图Sk(G)、三角剖分图T(G)和叠代三角剖分图Tk(G)的基尔霍夫指数；在文献[10]中，于越等人定义了两类图运算，并计算对应图RT(G)和H(G)的基尔霍夫指数；在文献[11]中，姚志远等人计算了幂超图和幂超点联图的基尔霍夫指数。

本文定义了一种新的图运算RKa(G)，它是将G的每条边变换为一个a阶的完全图Ka而得到的。第三节计算了RKa(G)各顶点对的电阻距离、基尔霍夫指数、度和与度积基尔霍夫指数，得到的RKa(G)这些指数的计算公式均是通过原图G的指数表达的。

1 电网络原理与相关引理

在计算电阻距离和基尔霍夫指数时，通常会用到电网络的几个基本原理——消去原理、割点原理、替代原理等。

消去原理[1]设B是连通图G的一个块且B含有G的一个割点w，记G′=G-{V(B)w}，则对于G′中任意两个顶点u和v，都有ΩG(u,v)=ΩG′(u,v)。

割点原理[1]若点w是连通图G的一个割点，u和v属于G-w不同的连通分支，则

对于复杂电网络，有时需要先作简化，如将电网络的一部分进行替代且保持整体性质不变，这就有了在电路中应用更为广泛的替代原理。在给出替代原理之前，先介绍S-等价的概念。

S-等价 设电网络G和G′的顶点集分别为V(G)和V(G′)，S⊆V(G)⋂V(G′)，如果∀u,v∈S，都有ΩG(u,v)=ΩG′(u,v)，则称电网络G和G′是S-等价的。特别地，当S=V(G)⋂V(G′)时，即电网络G和G′是V(G)⋂V(G′)-等价时，称G和G′是等价的电网络。

替代原理设H是G的一个子电网络，H和H′是V(H)-等价的，G′是将H′替代G中的H后得到的新的电网络，则∀u,v∈V(G)，均有ΩG′(u,v)=ΩG(u,v)，即G和G′是等价的电网络。

在复杂网络的替代简化中，完全图子电网络和星图子电网络的互相替代是比较常见的。

星网变换[19]设n阶完全图Kn是电网络G的一个子电网络，Kn的边电阻为1欧姆，将n+1阶星图Sn替换Kn后得到的新电网络G′和G是等价的，且其中Sn的边电阻为欧姆。

设G是一个具有m条边的连通图，剖分图S(G)是在G的每条边上添加一个顶点后得到的图，记V′=对于剖分图S(G)，文献[8-9]与[20]中有如下结论：

引理1[20]设G是一个连通图，剖分图S(G)中各顶点对的电阻距离为

引理2[8]设G是一个具有n个顶点，m条边的连通图，S(G)是其剖分图，则有

引理3[9]设G是一个具有n个顶点，m条边的连通图，d G(u)表示图G中顶点u的度，则有

2 主要结论

本节将给出RKa(G)各顶点对的电阻距离、基尔霍夫指数、度和与度积基尔霍夫指数，并得到这些指数与原图G的相应基尔霍夫指数之间的关系。

令连通图G的顶点集与边集分别为

其中，V1是图运算后新增点的集合。

图1 图C5和RK4(C5)

因为m个完全子图(i=1,2,…,m)的边电阻都是单位电阻，根据星网变换原理，星图(i=1,2,…,m)的边电阻为且图RKa(G)与是等价的，即当u,v∈RKa(G)时，有。

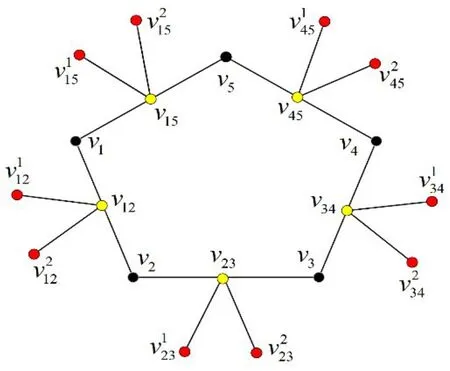
图2 图R(C5)

推论1设G是一个连通图，则图RKa(G)的各顶点对之间的电阻距离为

定理1设图G是一个具有n个顶点，m条边的连通图，则RKa(G)的基尔霍夫指数为

证明根据基尔霍夫指数的定义，有

由推论1中的（1）可知

由推论1中（2）的证明和引理3可知

由推论1中（3）的证明、（4）和引理2可知

综上所述

定理2设图G是一个具有n个顶点，m条边的连通图，则RKa(G)的度和基尔霍夫指数为

证明根据度和基尔霍夫指数的定义，有

由推论1中的（1）可知

由推论1中（2）的证明和引理3可知

由推论1中（3）的证明、（4）和引理2可知

综上所述

定理3设图G是一个具有n个顶点，m条边的连通图，则RKa(G)的度积基尔霍夫指数为

证明根据度积基尔霍夫指数的定义，有

由推论1中的（1）可知

由推论1中（2）的证明和引理3可知

由推论1中（3）的证明、（4）和引理2可知

文献[9]中讨论的三角剖分图T(G)可看成将连通图G的每一条边变成3阶的完全图K3得到的图。当a=3时，图RK3(G)≅T(G)。将a=3分别代入以上定理易得，如下推论。

推论2[9]设G是一个具有n个顶点，m条边的连通图，则三角剖分图T(G)的基尔霍夫指数，度和基尔霍夫指数和度积基尔霍夫指数分别为

文献[7]中讨论的脂环烃衍生物网络Tn(K5)可看成将n阶的圈Cn的每一条边变成5阶的完全图K5得到的图。

推论3[7]脂环烃衍生物网络Tn(K5)的基尔霍夫指数，度和基尔霍夫指数和度积基尔霍夫指数分别为

证明由Tn(K5)的构造可知Tn(K5)≅RK5(Cn)，将a=5，G替换成Cn代入定理1可得

同理可验证Kf+(Tn(K5))和Kf∗(Tn(K5))的值。

文献[6]中讨论的链式硅酸盐网络SiLn和环式硅酸盐网络可分别看成是将n阶的圈Cn、长为n的路Pn的每一条边变成4阶的完全图K4得到的图。

推论4[6]链式硅酸盐网络和环式硅酸盐网络的基尔霍夫指数分别为

证明由的构造可知将a=4，G替换成Pn代入定理1可得

∀u,v∈V(Pn)，满足ΩPn(u,v)=d Pn(u,v)，所以路Pn的基尔霍夫指数等于Wiener指数[21]，即Kf(Pn)=W(Pn)=，根据度和基尔霍夫指数和度积基尔霍夫指数的定义，不难得出

又因为|E(Pn)|=n，|V(Pn)|=n+1，所以

3 总 结

本文将无向连通图G的每条边变换为一个完全图Ka得到了新图RKa(G)，并用图G的不变量表示了RKa(G)各顶点对的电阻距离、基尔霍夫指数、度和以及度积基尔霍夫指数，同时利用得到的显性计算公式，验证了文献[6-7]和[9]中的已有结果，为这些特殊图的基尔霍夫指数计算提供了一种新的方法，简化了计算。

进一步考虑对无向连通图G的顶点进行图运算，如将每个顶点都变换为一个完全图或者一个圈等，得到新图G′。由于图G的每个顶点都是G′的割点，运用消去原理和割点原理，图G′的基尔霍夫指数是可以计算的。此外，对于图G的边进行其他图运算，如将图G的每条边变换为一个长为n阶的路，各顶点对的电阻距离以及基尔霍夫指数如何计算，尚待进一步研究。