最低工资与人力资本、物流业效率及产业结构关系的实证分析
江雨燕,张泽康,王付宇
(安徽工业大学 管理科学与工程学院,安徽 马鞍山 243032)
一、引言及文献综述
物流产业贯穿于整个商品生产、流通及消费过程,具有高度集成和深入融合商品流通加工、运输配送、仓储包装、信息管理等功能,是延伸各个产业链,提高产业链价值,打造现代产业体系的重要支撑,是提升国民经济循环效能的基础。“十三五”期间物流业实现平稳增长,物流效率进一步提升,降本增效成果显著。在“十四五”规划中,为应对新发展阶段的复杂形式,率先构建新发展格局,加快物流产业结构优化及实现物流业高质量发展,长三角地区将进一步全面推进物流产业降本增效。物流产业的降本增效除了依靠市场机制下各微观主体的竞争性自主创新外,还在很大程度上受到劳动力就业政策及财政政策的影响。最低工资制度长期以来都是政府及学界广泛关注的热点问题,在降本增效的大背景下,有必要对最低工资政策与物流业的发展进行深入的研究。
最低工资制度是国家以法律的形式对劳动力市场进行干预、保障低收入人群基本生活、调节市场活动及促进社会公平公正的重要手段。但伴随着最低工资标准的不断提高,高昂的劳动力成本无疑加大了物流产业降本工作的难度,尤其是对于早期依靠廉价劳动力发展的东部地区,当人口红利已不再成为竞争优势,将会对物流业发展产生怎样的影响?物流效率能否有效提升?物流产业结构能否进一步优化?基于此,探究最低工资对物流产业的影响效应,有助于实现物流业在新发展格局下的高质量发展。
现阶段,对物流业发展影响因素的研究从多方法、多角度展开。汪文生和考晓璇研究认为,经济发展水平与物流产业发展水平之间存在正相关的关系[1]。王健和刘荷以福建省为研究对象,发现区域经济发展能带动物流业发展[2]。秦愚和陈珍珠通过向量自回归模型揭示,第三产业有助于促进物流产业发展[3]。李琳用中国31个省的面板数据说明,金融集聚和金融发展对物流业发展有显著的促进作用[4]。冷俊峰和刘泳宇验证出产业集聚与物流效率之间存在显著的门槛效应,并揭示产业集聚程度的提升会不断削弱对物流效率的正向影响[5]。其次,除了上述经济因素外,也有学者关注于政府因素及政策影响。张煌强研究认为政治因素和经济因素对物流业发展影响最大,其中,政府为其发展给予的政策扶持和税收优惠是物流业发展的重要因素[6]。蔡海亚和徐盈之基于空间经济学视角,确定了物流产业发展与政府干预存在显著正相关[7]。刘承良和管明明研究表明,政府调控对物流业效率具有显著的正向影响[8]。然而,龚雪通过研究发现政府支持度与物流综合技术效率呈现出显著的负相关[9]。刘浩华和陈秀玲的实证结果显示,环境规制与创新的交互效应会显著阻碍物流业发展,在创新水平不高的情况下过强的环境规制会抑制物流业发展[10]。王静采用动态面板模型及混合面板模型实证检验出我国的扩张性货币政策会正向引导物流产业结构优化升级,紧缩性货币政策则具有倒逼效应[11]。影响物流业发展的因素还包括劳动效率[12]、人力资本[13]、物流业物质资本存量和从业人员占比[14]等。目前,国内外学者多从宏观经济、行业发展、政府支持等维度探讨对物流产业的影响,相关研究成果对把握物流业发展动因具有重要参考价值。
虽然有关物流产业发展的研究已在多方面展开,但围绕其影响因素的研究主要集中于经济因素,鲜有学者关注于劳动力政策对物流产业的影响,并且对其影响因素的探究多为静态分析,未能考虑到动态关系。最低工资制度作为世界普遍采用的制度,虽然具有改善社会贫富差距和收入结构的好处,但在一定程度上使得企业面临高昂的劳动力成本压力[15],改变企业的人力资源比例及结构,并通过减少人力资本投资缩减企业的存续时间[16],而物流行业的高质量发展需要更为专业化和集约化的分工,这也使得物流业易受到最低工资制度的影响。基于此,本文在理论分析的基础上,选取长三角地区为研究对象,从最低工资这一劳动力政策视角出发,构建贝叶斯向量自回归(BVAR)模型,以探究最低工资与人力资本、物流产业效率及物流产业结构的动态关系。
二、研究假设
(一)传导机制及研究假设
1.最低工资与人力资本
最低工资制度通过成本效应这一机制影响企业的员工配置[17],低学历低技能员工被企业辞退的可能性增加,以及不同技能劳动者获得报酬的差异,促使其不断优化自身技能或者投向更高的教育,从而促进劳动力素质的提升,提高劳动者的人力资本累积。另外,最低工资的实施或上调会改变企业员工比例及结构,增加对高技能员工的需求,进而优化企业人力资本。这就需要企业能迅速准确把握劳动力市场,及时补进高技能劳动者,但由于劳动力跨部门、跨行业或者跨区域流动所造成的差异性流动壁垒,使得企业在短时间内难以快速调整雇佣结构,从而抑制人力资本的优化。另一方面,为应对成本上升对利润的积压,企业可能会通过减少员工的培训力度或比例来缩减成本开支,这也将不利于人力资本的积累。因此,提出假设H1:
H1: 短期内最低工资对人力资本的积累具有抑制作用,长期则为促进作用。
2.最低工资与物流效率
最低工资对物流效率的影响效应主要表现在以下几个方面:第一,最低工资的上涨可能会通过“要素替代效应”提高物流效率。最低工资的直接影响是劳动力成本增加,企业通常采用资本或者技术代替劳动力,尤其是效率低下的企业更容易受到最低工资的冲击,故通过设备的更新升级及创新提高效率以抵消成本效应。第二,最低工资标准的提高拉动了社会平均工资的上涨以及市场需求的增加,通过“需求创造效应”提高企业的创新意愿,从而带动生产效率的提升。第三,从竞争角度出发,最低工资的提高使得低技能劳动者报酬上涨。在这种情况下,企业更愿意聘用高技能员工,代替低技能员工以此保持竞争优势,故员工技能水平的整体提高有助于促进效率的提高。此外,效率工资模型表明,工资的调高不仅能刺激员工提高生产率,还能增加其努力程度,从而自发提高效率。因此,提出以下假设H2:
H2:最低工资对物流效率提升具有促进作用。
3.最低工资与物流产业结构
最低工资标准有助于推动物流产业结构优化。较低的劳动力价格导致整个行业陷入“低技术陷阱”,抬高企业使用先进技术设备的临界点,对低廉劳动力价格过分长期依赖,促使企业逐渐丧失改革升级的动力,而最低工资标准的实施和上涨在一定程度上会倒逼企业进行技术研发和创新,从而优化产业结构。此外,低廉的劳动价格将阻碍整个物流行业的有序竞争,效率低下的企业无需提高生产工艺依然能保持可观利益。长此以往,行业内的有序竞争难以发挥作用。现有研究显示,最低工资的上涨有助于加快低生产率企业退出市场[19],阻碍低生产潜能企业的进入,最低工资制度促使行业发挥优胜劣汰的竞争机制,让先进生产效率的企业存活,效率和产品附加价值都低于行业平均水平的企业淘汰出局,将更多的存续空间留给高效率企业,最终促进产业结构升级。因此,提出以下假设H3:
H3:最低工资对物流产业结构优化具有促进作用。
(二)模型建立及指标说明
1.模型建立
选取最低工资、人力资本、物流产业效率、物流产业结构作为内生变量构建BVAR模型。VAR(P)模型的一般形式如下:
Yt=C+A1Yt-1+…+ApYt-p+εt
其中,t=1,2…,m、Yt是在t时刻内生变量、p为模型的滞后阶数、εt为白噪声序列,C和Ap为模型待估计系数矩阵。
经典的VAR模型虽然具有模型简洁、中短期预测效果较好的优点,但也存在估计参数过多的缺点。尤其是对于小样本来说,这一缺点更为明显,过多参数化问题可能会导致多重共线性及自由度的损失,从而降低估计效率和增大样本外预测误差,而贝叶斯理论能有效解决这一问题。与传统的估计方法不同,贝叶斯估计方法的基本思想是将待估计模型的参数视为随机变量,并服从一定的分布,然后根据经验给出待估计参数的先验分布,并将其结合样本信息,最后利用贝叶斯定理计算待估计参数的后验分布,从而用估计的参数得到估计值。考虑到本文样本数量较小,而贝叶斯方法有助于解决模型中超参数过多的问题,且拥有更好的预测效果,故建立BVAR模型,采用Minnestosa先验分布,利用BVAR模型做进一步的动态关系研究。
Minnestosa先验分布是对系数施加限制,假设它们较短滞后的系数更可能接近于零。限制条件是对所有系数指定零均值和小标准差的正态先验分布,随着滞后的增加,标准差减小,除了方程左边变量自身的一阶滞后变量的系数的先验期望为1外, 其他变量的先验期望均是0。模型中第i个方程第j个变量滞后p期的系数先验标准差由Si,j,p表示:

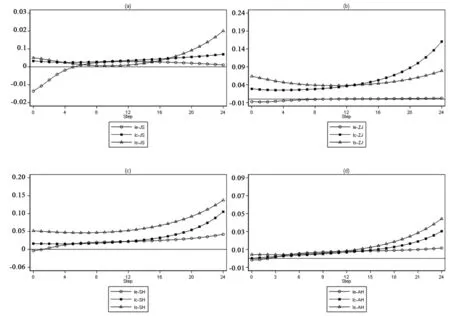
其中,γ为总体紧度,表示对先验信息把握的大小程度;g(p)衡量的是变量滞后p期相对于滞后1期的紧度,g(p)=p-d,d(d>0)是衰减系数;f(i,j)表示相对紧度,反映了第i个方程中变量j相对于变量i的紧度,当i=j时,f(i,j)=1,否则为wij(0 考虑限制性VAR模型的矩阵形式可以表示为: yt=ZtB′+εtt=1,2,…,m 将yt,Zt,B′和εt按转置排列,那么每个都是一个m×n的矩阵。方程可以写为: Y=ZB+ε,ε~Nmn(0,∑⊗In) 模型系数的Minnestosa先验分布可表示为: 在设置Minnestosa先验分布的基础上,利用Gibbs抽样得到待估计的参数,通过基于BVAR模型的脉冲响应函数和方差分解考察最低工资与人力资本、物流效率及产业结构之间的动态关系。 2.指标说明 本文主要涉及最低工资、人力资本、物流效率和物流产业结构四个变量。各变量数据选取如下: 最低工资。目前,我国最低工资主要采用小时最低工资和月最低工资标准,由于小时最低工资标准主要运用于非全职劳动者,全职劳动者主要使用月最低工资标准,因此,选用各省最高档月最低工资标准,以2000年为基期剔除物价指数得到实际的最低工资。 人力资本。劳动者可以通过教育、技能培训及经验等相应方式进行积累,同时,教育是最主要的途径,当前,对于人力资本的指标主要集中于企业培训,较少从劳动者自身出发。考虑到统计年鉴上并未直接给出衡量人力资本的指标,因此,选用普通高等学校在校学生数(万人)作为人力资本的代理指标。 物流效率。有关物流效率的测量方法主要有Malquist生产率指数、数据包络分析法(DEA)、随机前沿分析法(SFA)等。数据包络分析又包含规模报酬不变的DEA-CCR法和规模报酬可变的DEA-BCC法。由于规模报酬不变的情况较难实现,因此,选用规模报酬可变的DEA-BCC模型来测量物流综合技术效率,将交通运输、仓储和邮政业增加值和货运量作为物流业产出变量,将交通运输、仓储和邮政业固定资产投资作为资本投入,在职人数作为劳动要素投入。假设有n个决策单元,每个决策单元有m个投入和h个产出,xij(xij>0)表示第j个决策单元的第i种输入的投入量,yrj(yrj>0)表示第j个决策单元的第r种输出的产出量,设定第j个决策单元的DEA-BCC模型如下: 其中,θ表示决策单元的综合技术效率值、ε为阿基米德无穷小量、s-和s+分别表示投入松弛变量和产出松弛变量、x0和y0分别为决策单元的投入和产出、λj表示第j个决策单元的组合比例。各省市的物流效率测算结果如图1所示。 图1 各省物流效率 物流产业结构。有关产业结构指标的选取主要包含产业增加值与总增加值之比,产业就业人数与总就业人数之比等。考虑到本文侧重分析的物流产业为第三产业,并且,物流产业增加值是反映物流产业发展规模和水平的重要指标,故使用各省物流产业增加值占第三产业增加值的比例来衡量物流产业结构。 选取长三角地区2000年至2020年相关数据作为研究样本,历年数据来源于各省统计年鉴以及国泰安数据库,使用Stata17.0软件对最低工资、人力资本、物流效率、物流产业结构进行对数化处理以消除可能存在的异方差问题,并依次命名为lm、le、lc和ls。 为避免时间序列数据的伪回归现象,采用ADF单位根检验数据的平稳性。结果显示,除浙江省的lc、上海市的le及安徽省的lc能拒绝原假设外,其余原变量均不能拒绝存在单位根的原假设,故为非平稳时间序列。对各省原变量进行一阶差分后做ADF检验,结果见表1,由表可知各省一阶差分后的变量均能拒绝存在单位根的原假设,因此为一阶单整序列I(1),满足模型平稳性要求。 表1 ADF单位根检验 格兰杰因果关系检验是确定时间序列中两个变量间因果关系的常用方法,其定义是某一变量有助于解释另一变量的未来变化。格兰杰因果关系结果见表2。 表2 格兰杰因果关系检验结果 由表2可得江苏省的最低工资在1%的显著性水平下拒绝不是人力资本的格兰杰原因,即最低工资的变化会显著引起人力资本的变化,人力资本同样也在1%的显著性水平下拒绝不是最低工资的格兰杰原因,因此,人力资本与最低工资之间互为格兰杰原因,最低工资在5%的显著性水平下拒绝不是物流效率的格兰杰原因,在10%的显著性水平下拒绝不是物流产业结构的格兰杰原因,这表明最低工资的变化是物流效率及产业结构变化的原因;浙江省最低工资与人力资本互为格兰杰原因,在1%和5%的显著性水平下最低工资分别拒绝不是物流效率及物流产业结构的格兰杰原因;同样在1%和5%的显著性水平下,安徽省的结果与浙江省的结果相同,且最低工资与人力资本互为格兰杰原因;上海市的最低工资在1%的置信水平下显著为人力资本、物流效率及物流产业结构的格兰杰原因,同样,人力资本也在1%的置信水平下为最低工资的格兰杰原因。总体而言,长三角地区的最低工资变动均能显著影响人力资本、物流效率及产业结构的变动,并且,人力资本会引起最低工资的变动。 进一步验证最低工资与人力资本、物流效率及产业结构是否存在长期均衡关系,运用Johansen协整分析法进行检验。在检验前需要确定最优滞后阶数,常见的信息准则包括LL、LR、FPE、AIC、HQIC及SBIC,根据以上信息准则确定各省模型的最优滞后阶数为3。各省协整检验结果如表3、表4所示,其中江苏省与上海市分别存在三个协整方程,浙江省与安徽省存在两个协整方程,结果表明各省的最低工资与人力资本、物流效率及产业结构之间均存在长期稳定的均衡关系。 表3 江苏省和上海市协整检验结果 表4 浙江省和安徽省协整检验结果 构建BVAR模型,以此探究长三角地区最低工资与人力资本、物流效率及物流产业结构的动态关系,采用Minnestosa先验分布,将总体紧度设为0.1、相对紧度为0.4,并通过Gibbs抽样估计模型,MCMC迭代10000次、Burn-in为5000次。马尔可夫链是否收敛对模型估计的稳健性至关重要,由图2可见(限于篇幅所限仅给出部分结果),分别为系数lm的踪迹图、直方图、自相关函数、核密度图,抽样系数的马尔科夫链踪迹图都趋于稳定,前后两段的核密度图重合度很高,自相关函数快速衰减,收缩因子低于1.1,因此,可以判断通过MCMC方法估计的模型参数处于平稳的收敛状态,所构建的BVAR模型可信度很高。 图2 lm抽样系数诊断综合图 1.贝叶斯VAR模型脉冲响应函数 图3为各变量基于贝叶斯VAR模型的脉冲响应图,脉冲响应函数是分析系统内某一内生变量在受到自身及其他变量一个单位(或标准差)的冲击后所产生的响应。(a)(b)(c)(d)分别为江苏省、浙江省、上海市及安徽省人力资本、物流效率、物流产业结构对最低工资的脉冲响应,设定冲击作用的滞后期长度为24期,纵轴表示影响程度。 图3 各变量脉冲响应组合图 图3(a)为江苏省最低工资对人力资本、物流效率及产业结构的脉冲结果。其中,人力资本在受到最低工资一个标准差的冲击后,在当期表现为负向响应且达到最小值为-0.0135,并从第一期开始呈现出持续衰减的负向冲击作用,随后在第6期大于0,变为正向作用,表明在短期内上调最低工资会对人力资本积累产生一定程度的抑制效应,随着这种抑制效应逐渐减少并转变为促进效应,长期看来则有助于人力资本的积累;江苏省物流效率在受到最低工资冲击的影响后,物流效率在当期立即呈现出正向响应,随后微弱减弱,在第四期达到最小值后始终保持缓慢增长,表明江苏省最低工资的上调会导致省内物流效率的持续提升;物流产业结构对最低工资一个标准差冲击的当期响应为正,逐期递减至第10期达到最小值0.0006,随之继续呈现出增加势态,虽然短期内出现递减的正向趋势,但其影响程度总是大于0,因此,上调最低工资对于促进物流产业结构优化具有积极的正向作用。 图3(b)为浙江省最低工资对人力资本、物流效率及产业结构的脉冲结果。浙江省人力资本在受到最低工资一个标准差的冲击后,人力资本立刻做出一个负向响应,其影响程度为-0.007,随后逐渐减少至第10期变为正向影响,即浙江省的最低工资增加对人力资本积累的影响表现为前期抑制、后期促进的作用;物流效率在受到最低工资的冲击后,从当期开始表现为持续增长的正向影响,表明最低工资的增加对物流效率提升有积极的促进作用;物流产业结构对最低工资一个标准差冲击的反应为正,随后呈现出微弱的先降后升趋势,但其响应程度保持大于0,因此浙江省最低工资的增加对物流产业结构优化具有积极的促进作用。 图3(c) 为上海市最低工资对人力资本、物流效率及产业结构的脉冲结果。上海市人力资本在受到最低工资一个标准差的冲击后,当期表现为负向响应并达到最小值-0.0036,逐渐衰减至第3期转为正向影响,表明上海市最低工资的增长在前期不利于人力资本积累,后期则有助于人力资本积累;物流效率在当期对最低工资一个标准差冲击的表现为正(0.016),之后保持快速增长趋势,即上海市最低工资的增长能够促进物流效率提升,且这种积极作用随时间增加而增加;物流产业结构对最低工资一个标准差冲击的反应为正,衰减至第6期达到正向响应的最小值0.046,表现出先减少后增加的正向影响。总体而言,上海市最低工资的增长对物流产业结构优化有积极的正向作用。 图3(d) 为安徽省最低工资对人力资本、物流效率及产业结构的脉冲结果。安徽省人力资本在受到最低工资的一个标准差冲击后,最低工资对人力资本造成的影响为负向,其影响程度为-0.0018,随后这种负向变动逐渐消失,至第4期变为正向影响,表明在短期内最低工资的上升会减少人力资本的积累,长期而言则能促进人力资本积累;当给定最低工资一个标准差冲击时,安徽省物流效率虽然在当期表现出微弱的正向响应,但随后保持快速上升趋势,表明最低工资的上涨会不断促进物流效率的提高;当物流产业结构受到最低工资一个标准差的冲击后,最低工资对物流产业结构的影响为正并且持续上升,表明安徽省最低工资对物流产业结构的促进作用会随时间增加而不断上升。 总的来说,长三角地区最低工资上涨对人力资本积累的影响呈现出先抑制后促进的变化趋势。这可能是因为企业在短时间内难以把握劳动力市场,而采取减少人力资本投资或职工培训等方式来缓解劳动力成本的提高,但这种抑制效应会随着时间的推移逐渐消失最终演变为正向的促进效应;无论长短期,长三角地区的最低工资上涨均能促进物流效率提升以及物流产业结构的优化,故假设H1 、H2、 H3均成立。 2.贝叶斯VAR模型方差分解 方差分解是度量第i个内生变量对第l个内生变量影响的另一个方法,并且能反应各内生变量间冲击的影响程度。设定方差分解的滞后期为24期,由于本文侧重于最低工资对其余变量的影响,因此设定最低工资为冲击变量,度量最低工资对每个内生变量的贡献程度,图4中的(a)(b)(c)(d)分别为江苏、浙江、上海和安徽的方差分解图。 图4 各变量方差分解组合图 由图4(a)所示,对江苏省最低工资进行向前一期预测,其预测方差完全来自于最低工资本身(贡献率100%),受其自身波动影响方差的贡献从第2期开始逐渐下降,但在第24期依旧保持在67%左右;相比于物流效率和物流产业结构,最低工资对人力资本的贡献度相对较大,最低工资在第1期对人力资本的解释力为26.7%,也就是说人力资本预测方差的26.7%可由最低工资变动解释,随之整体上发生微弱的变化,但最低工资对人力资本的贡献度仍然保持在26%左右,说明最低工资对人力资本积累的影响程度较大;对物流效率进行向前一期预测,最低工资对其的贡献率大约为7.7%,其影响程度逐期增加,在第24期达到最大值(贡献率12.3%),说明最低工资对物流效率的正向影响会随着时间变化而增加;对物流产业结构进行向前一步预测,物流产业结构预测方差的8%可由最低工资解释,其解释力不断增加最终为16.8%,同样表明最低工资对物流产业结构的影响呈现出稳定增长势态。 如图4(b)所示,对浙江省最低工资进行向前一期预测,其自身的贡献率为100%,随之下降至59.7%;对浙江省人力资本、物流效率及产业结构各进行向前一步预测,受最低工资波动影响程度最大的为物流效率,最低工资的贡献度从第1期的20.9%逐渐上升到23.7%;最低工资对人力资本的解释度为16.9%,之后其解释力逐渐增加,并在第24期达到最大值(贡献率23%);浙江省物流产业结构预测方差的16.8%可由最低工资解释,最低工资对物流产业结构的贡献度由小变大,当滞后24期时,最低工资的贡献率为18.4%。 如图4(c)所示,对上海市最低工资进行向前一期的预测,其预测方差全部受自身波动的影响(贡献率100%),然后快速下降至37.1%;相比于人力资本和物流效率,前期最低工资对物流产业结构的贡献度最大,最低工资对物流产业结构的贡献率在第1期达到最大值为26.3%,从第1期后呈微弱衰减趋势,但23.3%以上的波动仍可由最低工资解释;最低工资对人力资本的贡献率从第9期开始高于对物流产业结构的贡献率,虽然最低工资对人力资本的贡献率在第1期减少,但从第2期后保持稳定增长趋势,表明最低工资对人力资本积累的影响会随着时间变化而占比越大;最低工资对物流效率的解释力呈微弱上涨趋势,其贡献率从9.5%上涨至12.8%,即最低工资将对物流效率的影响同样会愈发明显。 由图4(d)所示,对安徽省最低工资进行向前一期的预测,其自身的贡献率为100%,随之持续下降,但仍有64%以上的波动都可由自身来解释;与物流效率及物流产业结构相比,最低工资对人力资本的贡献度相对较大,在第1期的贡献率为9.5%,随后保持快速上涨直至24.1%,表明最低工资对人力资本存在较大影响;对物流效率及产业结构作向前一期预测,最低工资对两者预测方差的贡献率相近,分别为7.6%和 7.3%,从第1期后都保持缓慢增长的变动,在第24期时,安徽省物流效率预测方差的16.9%及物流产业结构预测方差的13.2%可由最低工资解释,表明安徽省最低工资对物流效率及物流产业结构的影响程度一直呈现出非常稳定的缓慢增长趋势。 通过协整检验、格兰杰因果检验以及贝叶斯VAR模型实证分析了江、浙、沪、皖等长三角地区最低工资标准与人力资本、物流效率及物流产业结构的动态关系。 结果表明: 第一,长三角地区的最低工资与人力资本互为格兰杰原因,人力资本的变动会引起最低工资的变动,人力资本与最低工资之间存在长期稳定的均衡关系;由脉冲响应函数可得,最低工资对人力资本的影响为先负后正,短期的负向变动可能是由于企业为应对劳动力成本上升而缩减人力投资支出,或是在劳动力市场分割的情况下,在短时间内难以做出调节,从而在短期内抑制人力资本的积累,但从长期来看最低工资会促进人力资本累积,表明长三角地区最低工资的上调会随着时间的推移对人力资本产生促进效应,从而提高劳动力市场的整体素质,未来也将迎来“人力资本高质量”发展的新阶段;由方差分解可得最低工资对人力资本的影响力在整体上呈现上涨趋势。 第二,最低工资在5%的显著性水平下为物流效率的格兰杰原因,两者存在显著的长期均衡关系;由脉冲响应函数可得物流效率对最低工资冲击的响应为正,并持续保持上升趋势,表明最低工资对物流效率的提升有积极的促进效应,随着长三角地区最低工资的调高会推动整体物流效率的提高,进而加快推进现代物流产业的高质量发展;方差分解也同样验证了这一点,显示最低工资对物流效率的影响随时间变化不断增加。 第三,最低工资是物流产业结构的格兰杰原因,两者之间存在长期均衡关系;由脉冲响应可得物流产业结构对最低工资冲击的反应为正向,虽然存在微弱变化趋势,但整体上为正向关系,表明上调最低工资对物流产业结构优化有积极的正向作用,由此可知,最低工资的上调能促使长三角地区物流行业的整体优化。 基于以上结论,提出以下建议: 第一,科学合理调整最低工资。最低工资的调整幅度和频率应当综合考虑各行业的发展状况、劳动力市场、企业的承受能力以及经济环境等方面,尤其是更易受到最低工资影响的劳动密集型行业,做到因地制宜、循序渐进、实事求是和杜绝盲目跟风攀比,不仅要确保经济成果全民共享,还要使其与各行业的发展相适应,从而避免因最低工资过高所导致的劳动力市场价格扭曲、企业成本压力过大等负面影响。 第二,应加快推进物流产业的配套扶持政策。加大对物流行业的配套支持政策和执行力度,积极发挥政府的引导作用,统筹利用税收减免、人才补贴、金融支持等方式,以此缓解企业在短期内压缩人力资本投资。挤出创新研发费用等行为,助力物流产业的提质增效,保障低收入人群的同时推动物流产业的高质量发展。 第三,政府仍要打破劳动力市场分割,破除劳动力市场的流动性壁垒。一方面,有助于推动劳动力要素的自由流动,避免高分割市场所造成的不同技能劳动者的供需失衡,收入差距过大等现象。另一方面,促使企业能在短时间内把握劳动力市场,从而准确迅速调整雇佣结构以及要素投入比列,减少最低工资上涨后的短期不利效应。


三、实证分析
(一)平稳性检验
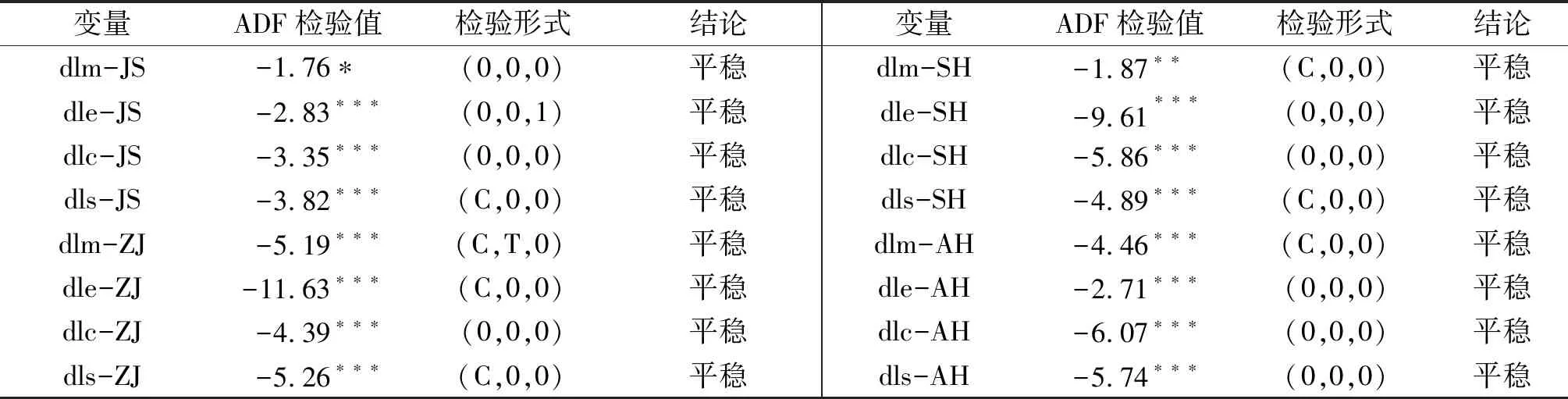
(二)格兰杰因果关系检验
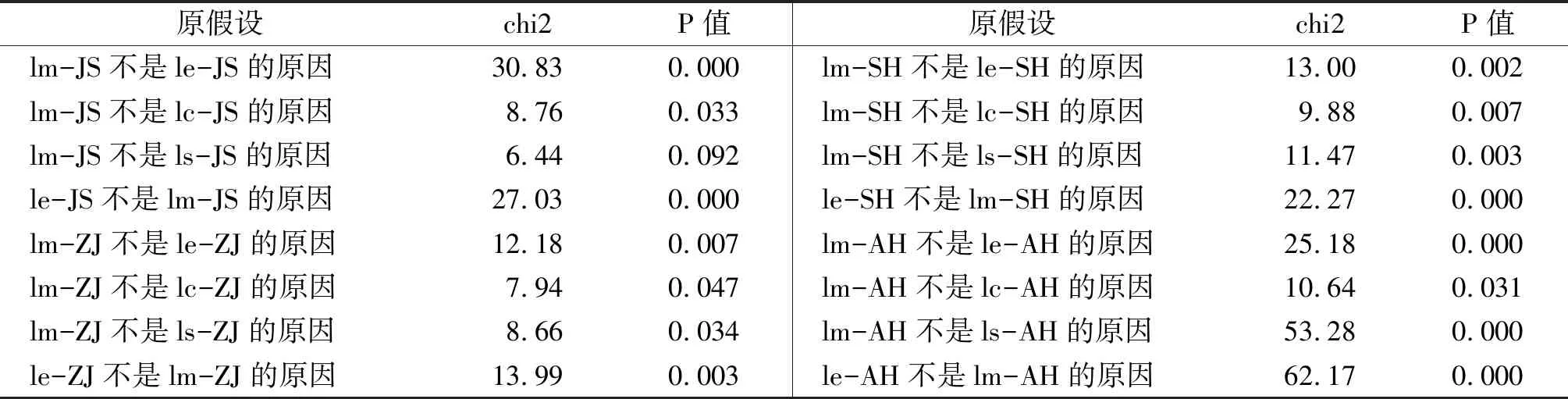
(三)协整检验


(四)BVAR模型估计


五、结论与建议

