基于数据融合和PSO的移动目标跟踪方法

赵远方

(驻马店职业技术学院,河南 驻马店 463000)

1 引言

无线传感器网络(WSN)是由多个低功耗、微型化的传感器节点以自组织的方式组成,广泛应用于军事及民用领域。在这些领域中,WSN节点被安放在监控区域,它们相互合作,进行信息的感知、监控和跟踪。随着目标跟踪理论的发展,许多方法在提高跟踪精度,保障跟踪的可靠性上得到运用。邬春明等[1]提出了结合实时数据修正的鱼群优化粒子算法,结果表明该算法在目标跟踪上精度和稳定性更优。吴冰[2]提出一种改进的EK-MTDC算法,结果表明能有效地提高目标跟踪效率。张英坤[3]研究了强跟踪算法与传统算法的区别,结果表明强跟踪算法在室内目标跟踪上优势更大。吴晓平等[4]针对移动目标的捕获问题提出了ULLS、CLLS、SDP三种算法,仿真证明三种算法中CLLS算法的误差最小。孙彦景[5]对比提出的ASFTT算法和几种自适应决策算法,通过采用标准数据集仿真表明提出的算法在目标跟踪的准确性和稳定性上更好。然而在无线传感器网络中,网络节点由蓄电池供电,该电池不能充电且一般无法更换,是影响节点和网络寿命的主要部件。因此,能耗节约式WSN在设计过程中是必须要考虑的关键[6]。在能耗方面,采用粒子滤波算法提前一步进行预测,[7]采用无极卡尔曼滤波算法进行提前预估[8]等,文献使用数据融合技术来提高检测性能[9]。但是,上述算法对于高度非线性过程的处理效果都不太理想。

通过以上分析发现,国内外学者在在目标跟踪准确性的算法上作了广泛的研究。但是在降低节点损耗、节省传感器数量上的研究较少。基于此,本文提出一种新的改进算法,即通过在一定区域内随机预布置若干传感器节点,动态设定父节点,并以父节点为中心,以部署半径R作圆构为部署区域,确定部署区域之后,将由父节点唤醒一切位于部署区域的传感器节点,运用粒子群算法[10]进行优化部署,与此同时将节点探测信息进行数据融合,从而利用较少的节点得到较高的覆盖率。理论计算后利用MATLAB软件验证结果。

2 理论模型

2.1 无线传感器节点感知模型

节点的感知模型表征了节点的感知半径和测定能力,是由传感器自身的物理特性决定的。本文研究移动目标的跟踪问题,因此,为了便于探测到移动目标,采用全向感知模型。传感器节点感知模型如图1所示,可以看出感知能力会随着距离的增加而减小,而且感知的不确定性也会随之增加。

图1 传感器节点概率感知模型

其中,R是节点确定感知半径,R1-R为概率感知范围.假设移动目标节点n到传感器节点S的欧式距离为d(s,n),移动目标节点被传感器节点S探测到的概率为p(s,n),则当d(s,n)≤R时,移动目标节点P被传感器节点S确定感知,此时p(s,n)=1;当d(s,p)≥R1时,移动目标节点P不能被传感器节点S感知到,此时p(s,n)=0,当R≤d(s,n) ≤R1时,移动目标P被节点S感知到的概率p(s,n)=e-λ[d(s,n)-R],具体如下面公式所示:

其中,λ为相关系数,假设传感器节点s坐标为(xs,ys),目标节点n坐标为(xn,yn),则二者之间欧氏距离d(s,n)可表示为:

(2)

2.2 数据融合模型

数据融合模采用D-S理论,它是贝叶斯方法的一种发展,与传统的概率论方法相比,它能够快速掌握问题的不可知性和不确定性[11]。在无线传感器网络中,待测目标有可能出现在传感器节点的确定感知区域,也有可能出现在传感器节点的概率感知区域。假设传感器节点A、B、C的位置关系如图2所示。

图2 数据融合模型

3 跟踪算法

3.1 传感器节点唤醒机制

本文所提算法中,假定所有传感器节点的初始工作状态为半休眠,所谓半休眠指的是传感器节点每隔时间T进行一次探测,除此之外的时间均处在不工作状态,以节省能量,当移动目标S移动到探测范围内时,总会有一个随机的传感器节点N探测到目标出现。定义第一个探测到目标的传感器节点为父节点Nf,当父节点确定之后,由父节点发出唤醒信号,唤醒的节点是以父节点为中心,在半径为RL的圆形范围内的所有传感器节点,使这些节点由半休眠状态转变到工作状态。随着移动目标的移动,现有的父节点Nf并不能保证它是距离移动目标最近的那个节点,为了解决这个问题,将这些节点的位置信息存储在一个矩阵Wn中,以时间T为周期,周期性的对比它们之间与移动目标之间的欧式距离Dn,同时更新位置矩阵信息,并将距离移动节点最近的传感器节点任命为新的父节点,直至移动目标的运动范围超出所有节点的探测区域,如公式(4)所示。具体如图3所示。

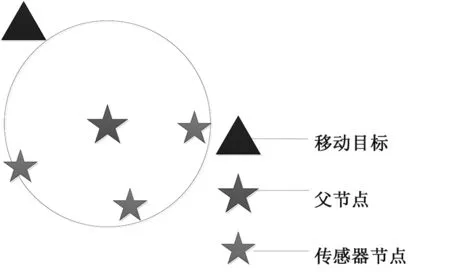
图3 传感器节点唤醒模型

假设传感器节点n坐标为(xn,yn),则它到目标节点S(xs,ys)的欧氏距离Dn为:

(3)

(4)

公式(4)中,Nf表示下一刻的父节点,Dn、Dm分别表示传感器节点n、m到移动目标S的欧氏距离,Nfn、Nfm分别表示父节点为传感器节点n、m。

3.2 基于PSO算法的目标跟踪

在对目标跟踪的过程中,更关心的是移动目标所经过路径的覆盖情况,而不是像整体覆盖那样,需要整个区域的覆盖率整体最高。而PSO算法的原理正是模拟鸟类寻食的行为,正好能够用来进行对移动目标的跟踪。由图3可知,当父节点Nf探测到目标的时候,其余三个传感器节点并不能探测到目标,此时,我们对这四个节点运用PSO算法,结合D-S证据理论,在父节点没有更换的前提下,保持对目标节点的实时跟踪。假设在n*T时间,父节点发生了变更,那么继续以新的父节点为中心,进行新一轮的PSO算法优化。将此过程以周期T不断地重复进行,即可实现用尽可能少的传感器节点对移动目标S的有效跟踪。

为了达到节能的目的,本文选用局部PSO算法,通过设置gbest和ω,实现对微粒飞行速度的有效控制与调整,使微粒只跟踪自身最佳位置和拓扑邻域中所有微粒的最佳位置,并不跟踪群体最佳位置,其速度更新公式如下:

vi,j(t+1)=ω·vi,j(t)+c1r1[pi,j-xi,j(t)]+c2r2[p1,j-xi,j(t)]

(5)

位置更新公式如下:

xi,j(t+1)=xi,j(t)+vi,j(t+1),j=1,2…d

(6)

其中ω为惯性权重系数,c1、c2为正的学习因子,r1、r2为0到1之间随机均匀分布的随机数,Pi=[pi,1,pi,2,…pi,d]为局部邻域中的最佳位置。

算法流程图如下(图4):

图4 跟踪算法流程图

4 实验结果与分析

采用Matlab R2014a进行仿真,设定探测区域是边长l=500m的正方形区域,传感器确定感知半径R=30m,概率感知半径R1=50m,以父节点为中心的唤醒半径RL=3*R=90m,传感器个数n=20,学习因子c1=c2=1.4962,惯性权重系数ω=0.7298,迭代次数N=10,通过用一条已知的曲线模拟移动目标的移动轨迹,仿真结果如图5、6、7所示。

图5 初始状态传感器分布

图6 移动节点位于待测区域内时传感器分布

图7 移动节点移出待测范围之后传感器分布

图5、6、7分别显示了移动节点处于不同位置时的传感器节点分布情况,从图中可以明显看出,只有位于移动节点经过的路径附近的传感器节点才会参与到目标的跟踪过程中来,其余传感器节点自移动节点从右下方进入探测区域到从左上方离开探测区域这段时间内都没有参与目标跟踪,它们的位置没有发生任何变化,并且在实现跟踪的过程中,只会调动父节点附近的传感器节点进行小范围的移动,这样就能实现节能传感器节点能量,延长传感器网络寿命的目的。

5 结论

针对目标跟踪的传感器能量损耗问题,通过采用动态选取父节点的方法,结合粒子群算法,将传统的大范围内优化转变为以父节点为中心的小范围内的节点位置优化,通过以父节点为中心的若干传感器之间的相互协作以及数据融合,从而有效地实现了目标的精确跟踪,同时又因为只有少量节点参与到目标跟踪中来,因此可以有效节约传感器节点消耗在节点移动上的能量,拓宽网络生命周期。仿真结果表明,本文提出的算法与传统算法比较,在实现对机动目标的高精度跟踪的同时可以有效地减少自身能量损耗。