基于GFRFs的非线性系统结构故障检测方法

史 洪 岩, 杨 文 奎, 潘 多 涛

( 1.沈阳化工大学 信息工程学院, 辽宁 沈阳 110142;2.沈阳化工大学 辽宁省化工过程控制技术重点实验室, 辽宁 沈阳 110142 )

0 引 言

非线性系统结构发生故障是造成系统无法正常运行的最大因素,目前基于振动的检测方法检测系统结构故障是较为有效且方便的方法[1-2]。

基于振动的检测方法可分为线性方法和非线性方法。应用线性方法时,通常使用有限元技术来评估损伤对受检结构模态特性的影响;基于一些先验知识,从使用振动信号估计的结构模态特性中检测损伤及其位置[3]。但是系统故障检测结果并不总是可靠,并且可能显示出对故障的低灵敏度[4]。近年来,开发基于非线性振动的故障检测方法备受重视[5-6],但由于其模型的选取不能完全表征出系统的非线性特性,导致后续的分析不够全面,对诊断结果有一定的影响。当故障检测领域向着复杂系统延伸,振动信号有着较强的非线性、非平稳以及非高斯等复杂特性,时域分析变得非常复杂,所以研究人员开始利用频域特性进行故障检测[7-8]。虽然利用频域分析的方法对系统特征进行了评定,但还是没有完全脱离时域分析,在应用中很难对复杂特征进行准确表述。

系统故障的存在通常会将非线性引入结构特性,由此产生的非线性效应往往对故障非常敏感。在现有的一些故障检测方法中,由于其采用的模型或者检测指标不太准确,可能导致检测结果会出现偏差。针对这些问题,本文提出了一种新的故障检测方法。该方法使用非线性系统的NARX模型,对GFRFs进行分析解决系统故障检测问题。

1 非线性系统的NARX模型和GFRFs

1.1 非线性系统的NARX模型

非线性系统的NARX模型[9]可以表示为

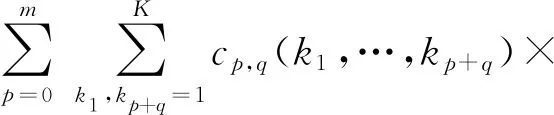
(1)

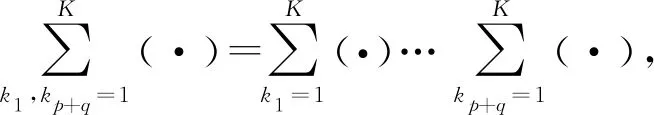
1.2 非线性系统的GFRFs

具有稳定零平衡点的非线性系统在平衡点附近可以用Volterra级数表示为

(2)

式中：hn(τ1,…,τn)被称为n阶Volterra级数核,N是非线性系统的最大阶数。

对于一个能够表述为Volterra级数的非线性系统,对n阶Volterra级数核函数hn(τ1,…,τn)进行多维傅立叶变换[10]得到GFRFs,如式(3)所示。

e-j(ω1τ1+…+ωnτn)dτ1…dτn

(3)

根据GFRFs理论,Zhu等[11]利用非线性系统的GFRFs推导的非线性系统输出频率响应表达式如式(4)所示。

(4)

式中：Y(jω)为输出频谱,U(jω)为输入频谱,σωn为满足ω1+…+ωn=ω的频域积分域。式(4)反映了在外带输入激励的非线性系统中,输出频率响应与系统的广义频率响应函数之间的数学关系。

2 非线性系统GFRFs的递推算法

2.1 谐波探测法

由式(1)NARX模型可得：

(5)

根据Peyton-Jones和Billings[12]提出的谐波探测法,可得：

Hn(jω1,…,jωn)=

(6)

式中：

Hn-i,p-1(jωi+1,…,jωn)×

exp[-j(ω1+…+ωi)lp]

Hn,1(jω1,…,jωn)=Hn(jω1,…,jωn)×

exp[-j(ω1+…+ωn)l1]

2.2 高阶GFRFs的递推算法

从理论上讲,非线性系统的GFRFs可以使用式(6)从NARX模型评估到任意阶,但实际计算过程相当耗时,通常只能使用二阶GFRF的结果。舍弃了高阶的GFRFs所得到的分析结果可能对系统内部特性产生偏差。因此Jing等[13]提出了一种能够估算出各阶次GFRF边界数值的递推算法。该算法可以根据模型参数和一阶GFRF估算出NARX模型的任意阶GFRF的大小范围,如式(7)所示。

定义

(7)

式中：C(p,q)表示一个非负函数的系数,cp,q(*)中的p和q满足0≤p,q≤n,n为阶数。

令：

Hn,0(·)=0,n>0

Hn,p(·)=0,n

(8)

式中：Rω表示一个NARX模型的输入频率范围,sup表示最小上界。

基于式(7)、式(8)可以得到[13]：

(9)

可见,高阶GFRF能够被低阶的GFRFs通过递推计算得到。引用文献[13]中定义的运算符号⊗和⊕,得到式(5)的NARX模型的n阶GFRF为

(10)

式中：系数bn0,bn1,…,bnm是一串非负的标量值,且

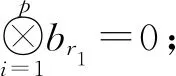
可见,第n阶GFRF的大小可以由一阶GFRF H1(jw)的大小和级为n的多项式函数来界定,多项式的系数是模型参数的函数。

3 基于GFRFs的故障检测原理

非线性系统中的故障会改变系统的非线性特性。当系统发生故障时,会导致系统的结构特性发生改变。NARX模型可以用来表示复杂结构非线性系统的动态特性[14],系统结构特性的任何故障引起的变化都可以通过已确定的系统NARX模型反映出来[15-16]。无论检测结构系统的NARX模型有多少种不同的形式,也不管NARX模型有多复杂,只要该模型能够正确捕捉系统的动态行为,相应的频率响应特性将是相同的,频域系统表示也将是相同的。因此,NARX模型的频域特征是受检结构系统状态的更好指标。

故障检测指标定义为

(11)

式中：Hi表示故障检测指标,SFi表示被检系统故障状态指标,SNi表示被检系统正常状态指标。

根据文献[12]中的损害指数定义,非线性系统的故障损害程度指数为

(12)

式中：Hi(jω)为受检系统的GFRFs,DF为系统的故障程度,DF越大说明系统的故障程度越高。

本文提出基于GFRFs的故障检测方法：识别系统的NARX模型;利用第2节GFRFs递推算法计算系统的GFRFs;将受检系统的GFRFs与无故障系统的GFRFs相比较,判断受检系统是否故障;根据DF评估系统的故障情况。

4 结果与分析

根据实验数据为受检系统建立NARX模型,通过PC、函数发生器和功率放大器生成频谱在0～2 MHz的检测信号,该检测信号应用于发射传感器以激励被检测铝板。铝板的响应是由HP示波器与PC和HP采集软件BenchLink结合获得。以10 MHz的频率对输入和输出信号进行采样,以生成数据进行分析。

在实验装置下,在3块铝板上进行了实验,其中铝板A未受损,铝板B具有直径2 mm的孔,铝板C具有尺寸为10 mm×0.4 mm的缝隙。图1显示了发射(T)和接收(R)传感器在铝板上的位置,以及受损板中损伤的位置、方向、尺寸和几何形状。

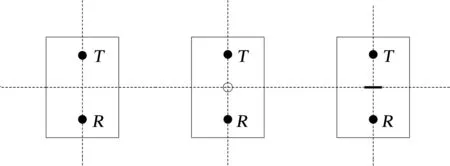
(a) 铝板A (b) 铝板B (c) 铝板C

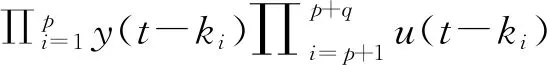
铝板A的NARX模型[12]为

y(t)=-0.188 609y(t-5)-0.179 285y(t-10)-

0.165 369y(t-15)-0.050 602 5y(t-20)-

0.031 084 7u(t-33)-0.027 581 5u(t-43)+

0.020 779 6u(t-37)+0.039 214 3u(t-46)-

0.039 371 4u(t-22)-0.004 479 23u(t-27)-

0.002 726 73u(t-52)+0.025 924 1u(t-55)-

0.028 602 3u(t-49)-0.009 271 74y(t-68)+

0.022 983 1u(t-16)-0.011 982 5u(t-10)-

0.045 582 1u(t-74)+0.019 449 8u(t-72)-

0.002 290 8y(t-84)+0.031 310 7u(t-76)-

0.008 987 67u(t-68)+0.806 869y(t-1)-

0.105 214y(t-2)-0.202 835y(t-9)-

0.434 581y(t-3)-0.043 930 1u(t-59)-

0.292 615y(t-4)+0.012 554 2y(t-54)-

0.028 609 2u(t-79)-0.005 068 64u(t-60)-

0.002 320 14u(t-9)+0.038 387 3u(t-28)-

0.139 759y(t-8)-0.005 142 84y(t-96)+

0.008 227 17y(t-4)y(t-4)-

0.033 786 9y(t-1)y(t-3)y(t-4)+

0.021 919 9u(t-78)-

0.022 478 2y(t-7)u(t-7)u(t-7)+

0.037 248u(t-61)+

0.007 121 55u(t-4)u(t-4)+

0.010 303 3u(t-19)+

0.027 122 3y(t-4)y(t-7)u(t-1)+

0.006 666 37u(t-2)

(13)

另外两种铝板的NARX模型可以参考文献[12]。根据式(6),可以求得：

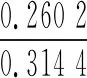
根据公式(10),可以求得：

|H2(jω1,jω2)|≤

依次类推,可以估算出任意阶的GFRF。但由于高阶GFRFs计算较为复杂且越高阶数值越小,对故障检测意义不大,因此求得前四阶的GFRFs,结果见表1。

表1 不同状态铝板的GFRFsTab.1 GFRFs of aluminum plates in different states

将基于GFRFs检测方法与文献[12]中的非线性输入频率响应函数(nonlinear output frequency response function,NOFRF)检测方法的各阶检测指标进行比对,结果见表2。

表2 GFRFs和NOFRFs检测方法的检测指标Tab.2 Detection indicators of GFRFs and NOFRFs

通过比较表2中三种不同状态铝板的一阶指标值可知,两种检测方法中无损害铝板的一阶指标值要明显大于另外两种铝板的一阶指标值,由此可以判断出铝板本身发生了结构性故障,说明了两种方法都能对故障情况进行有效的检测。同时发现,铝板B相比于铝板C,一阶指标值的变化更大,表明在带2 mm孔的情况下,对铝板非线性特征的影响更加显著。在这一点上,两种检测方法的检测结果也一致。

基于NOFRFs和GFRFs检测方法的故障损害程度指数见表3。

表3 GFRFs和NOFRFs检测方法的故障损害程度指数Tab.3 Fault damage indexes of GFRFs and NOFRFs

通过观察两种检测方法的DF,i,可知两种方法都对铝板的损害程度有着较好的检测效果。通过比较DF的大小,可以看出基于GFRFs的故障检测方法对系统故障更加敏感,能够更容易地检测出系统故障。而且通过比较GFRFs检测方法两种不同状态铝板的DF,可以看出带2 mm孔铝板的DF要大于带10 mm×0.4 mm缝隙的铝板的DF,说明带2 mm孔的铝板对系统的动态影响更加显著,与表2结果相符。相反,比较NOFRF检测方法两种不同状态铝板的值,结果跟表2不一致,这也表明了基于NOFRF的检测方法准确性较差。

为了能够更加显著地表明该方法的优越性,分别使用文献[12]、[15]、[16]中提出的方法对A、B、C 3种不同工况的铝板进行故障检测,利用式(11)计算出各个方法的故障检测指标值,得到的结果如图2所示。

图2 4种检测方法的故障检测指标Fig.2 The fault detection indicators of four detection methods

纵坐标表示4种方法的故障检测指标,本文使用GFRFs检测方法。文献[12]使用的为NOFRFs检测方法。文献[15]使用的为分布式故障检测(distributed fault detection,DFD)方法。文献[16]中使用的为基于NARX-network的故障检测方法。

由图2可见,4种方法都能实现对系统结构的故障检测,但通过对比可以很明显地得出GFRFs检测方法的指标值对故障的反应变化最大,说明基于GFRFs的故障检测方法检测指标对故障最为敏感。文献[15]、[16]虽然也是基于NARX模型所提出的故障检测方法,但其在后续的分析中并没有完全探究NARX模型中所包含的非线性特征,效果并不理想。虽然基于NOFRFs的检测方法与基于GFRFs的检测方法都是直接对NARX模型做检测分析,但由于NOFRFs引入了输入特征导致在对其进行计算时更为复杂,所以效果也不是很好。基于GFRFs的故障检测方法更加具有优势。

5 结 论

所提出的一种基于NARX模型的GFRFs系统结构故障检测新方法根据已建立的NARX模型中的模型参数和一阶GFRF,确定受检系统的任意阶GFRF,解决了高阶GFRFs由于其表达式具有多维性导致很难在实际应用中显示和解释的问题。通过比较受检系统的GFRFs数值和无故障系统的GFRFs数值,实现了系统故障检测。根据受检系统的GFRFs和无故障系统的GFRFs,确定系统故障损害程度指数,进一步对故障损害程度做出了有效评估。验证了所提出的方法的有效性。该方法与已有的故障检测方法相比,在准确性上具有显著优势。