ELM响应面在大跨度刚构桥悬臂施工可靠度研究中的应用
谢 旭,曹宇辞
(1.湖南联智科技股份有限公司,湖南 长沙 410203;2.湖南省交通科学研究院有限公司,湖南 长沙 410015)
1 结构可靠度分析
1.1 混合有限元模型建立
沱江大桥上部构造为(66+120+66)m预应力混凝土连续刚构,主梁采用变截面箱型截面梁,下部构造为薄壁墩、肋式台配桩基础。桥宽组成为:0.5 m(护栏)+11 m(行车道)+0.5(护栏),设计荷载等级为公路-I级。主梁采用C50混凝土,普通钢筋采用HRB335级带肋钢筋、HPB235光圆钢筋,纵向预应力采用标准抗拉强度为1 860 MPa的高强低松弛钢绞线。
采用有限元软件midas Civil建立全桥带悬臂施工阶段的有限元数值计算模型,根据该桥上部结构的实际构造和施工过程进行结构离散,主梁及下部墩柱结构均采用梁单元进行模拟,全桥共划分为96个单元,107个节点。
1.2 施工阶段可靠度分析
大跨度连续刚构桥悬臂施工阶段的线形控制是施工监控中的重点内容,实际施工中,刚构桥悬臂端由短变长,桥梁整体受力情况不断发生改变,不同节段箱梁的混凝土强度、弹性模量等参数也会对结构受力产生一定的影响,从而导致施工阶段悬臂端挠度的变化。为在确保结构可靠度的基础上最大限度地降低挠度偏差对主梁线形带来的影响,建立大跨度刚构桥悬臂施工阶段由悬臂段标高控制的主梁功能函数G见公式(1)。
G(t)=u(t)-|v(t)-v0(t)|
(1)
式中:u(t)为随施工期变化的大跨度刚构桥悬臂端挠度偏差容许值;v(t)为考虑随机变量变异的悬臂端挠度计算值;v0(t)为悬臂端挠度理论计算值。
2 极限学习机响应面建立
2.1 极限学习机基本原理
极限学习机(Extreme Learning Machine,ELM)是一种单隐含层的前馈型神经网络(Single-hidden layer feed forward neural networks,SLFN)[1,2],与普通神经网络不同,单隐含层的前馈型神经网络在网络结构上仅含有一个隐含层,故其在保证拟合能力的同时可以大幅提高对于样本数据的学习泛化能力,相比于传统BP神经网络,极限学习机无需反复调节迭代网络参数,有效降低了训练时间,提升了训练速度。
假设存在N个样本的训练集D={X,Y},X=(x1,x2,…,xN),Y=(y1,y2,…,yN),其中X为输入向量,Y为输出向量,采用m个神经元连接的极限学习机网络结构。
极限学习机网络结构由三部分组成,分别为输入变量组成的输入层、输出变量组成的输出层和连接输入、输出变量的隐含层神经元。极限学习机的网络映射关系见公式(2)。
(2)
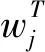
将极限学习机的映射关系表示为矩阵形式见公式(3)。
Hβ=Y
(3)
式中:H为隐含层输出矩阵;β为神经元输出权值。
隐含层输出矩阵H及神经元输出权值β可分别见公式(4)、公式(5)。
(4)
β=[β1,β2,…,βm]
(5)
此时,为求得神经元输出权值β,对矩阵进行运算见公式(6)。
β=H-1Y
(6)
式中:H-1为隐含层输出矩阵的广义逆矩阵。
2.2 高斯径向基激活函数
极限学习机网络结构中隐含层激活函数有多种形式,本文选取高斯径向基函数作为隐含层激活函数。径向基函数取值取决于样本中心点。
φ(r)=φ(‖x-c‖)
(7)
式中:φ(r)为激活函数;c为样本中心点。
其中,高斯径向基激活函数的具体表达式见公式(8)。
φ(r)=e(-r2)/2σ2
(8)
径向基的核函数表达式见公式(9)。
(9)
式中:k为核函数;d为核函数宽度系数。
此时,极限学习机响应面的线性方程组可通过高斯径向基激活函数见公式(10)。
Y=φβT
(10)
根据矩阵运算可推导神经元输出权值β为
β0=φ-1Y
(11)
式中:β0为β经训练后的输出权值。
求得训练后的神经元输出权值即可构建基于高斯径向基的极限学习机响应面模型。
2.3 ELM响应面模型训练
基于有限元模型生成大跨度预应力钢筋混凝土刚构桥的训练集和测试集。为研究刚构桥在施工过程中由材料及外界荷载变化引起的端部挠度变化规律,确保刚构桥施工过程中端部挠度在容许范围之内,并分析悬臂施工时的挠度失效概率及可靠度指标,提高极限学习机对刚构桥结构响应的拟合精度,降低结构响应拟合误差,本文选取施工期四种典型随机变量特征进行分析[3,4],四种随机变量均采用正态分布形式,其基本统计特征见表1。
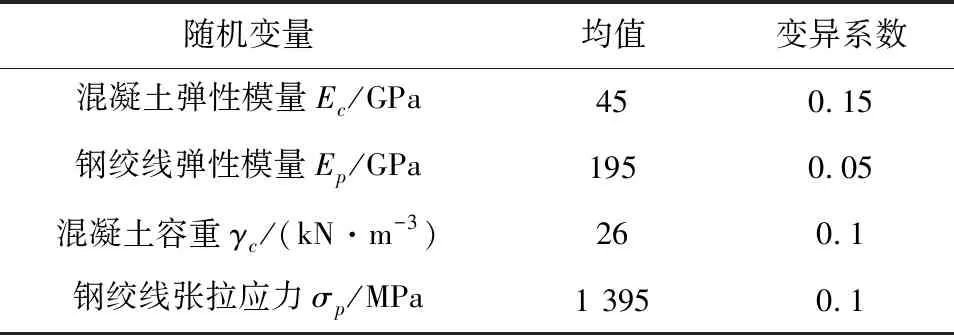
表1 随机变量分布特征
根据拉丁超立方抽样原则,采用有限元数值计算模型生成随机变量在均值上下限三倍标准差区间内的样本数据40组,其中前30组作为极限学习机响应面模型的训练样本,后10组作为极限学习机训练结果的验证集。
3 结果分析
基于MATLAB 2018b平台建立大跨度刚构桥的极限学习机训练程序,根据训练集样本拟合最佳的隐含层神经元权值,10组测试集的拟合结果见图1。由图1可知,极限学习机响应面模型的训练效果良好,对于10组测试集的拟合精度较高,相较于有限元模型的理论计算结果,10组测试集的最大拟合误差仅为5.37%,平均拟合误差仅为2.01%,证明了极限学习机响应面模型对不同工况下的刚构桥响应量预测精度满足可靠度分析的要求。
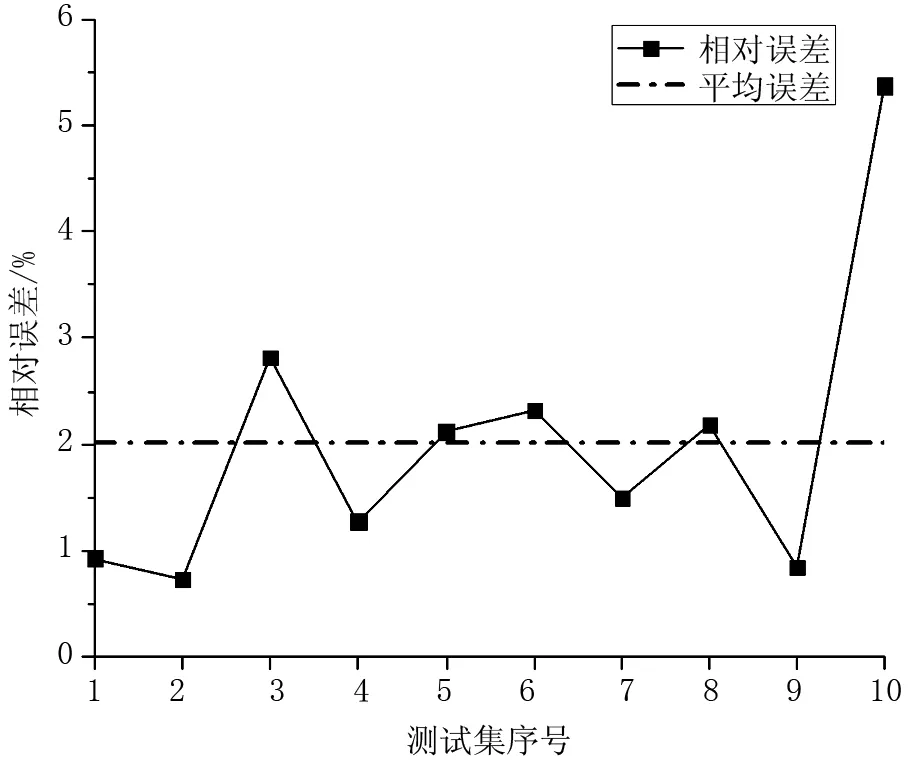
图1 极限学习机拟合结果
为验证极限学习机对于大跨度刚构桥的结构响应的拟合精度,引入标准支持向量机算法对相同样本数据进行学习拟合,采用同样10组验证集对二者的拟合精度进行检验,极限学习机和支持向量机相对有限元模型的拟合相对误差结果见图2。由图2可知,SVM的平均绝对相对误差为3.95%,ELM相较于SVM拟合精度更加稳定,拟合误差更低,且ELM由于网络结构相对更简单,无需调整更多的超参数,故训练效率更高。
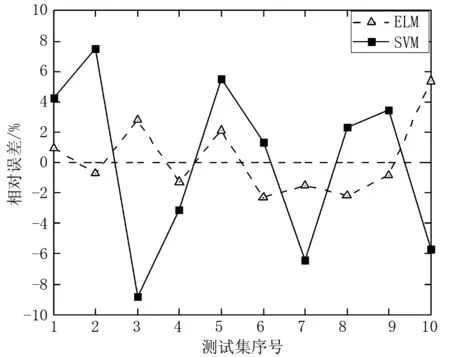
图2 SVM和ELM拟合误差对比
各悬臂施工工况下不同挠度容许值与结构可靠度的关系曲线见图3。由图3可知,各悬臂施工阶段结构可靠度与悬臂端容许挠度在一定区间内大致呈线性相关关系。对于短悬臂施工阶段,当悬臂端容许挠度小于1 mm时,结构可靠度指标小于1,结构失效概率较大;当悬臂端容许挠度大于5 mm时,结构可靠度指标较高,结构失效概率较小。对于中悬臂施工阶段,当悬臂端容许挠度小于4 mm时,结构可靠度指标小于2,结构失效概率较大;当悬臂端容许挠度大于12 mm时,结构可靠度指标较高,结构失效概率趋于0。对于长悬臂施工阶段,当悬臂端容许挠度小于10 mm时,结构可靠度指标小于1,结构失效概率较大;当悬臂端容许挠度大于24 mm时,结构可靠度指标较高,失效概率较低。
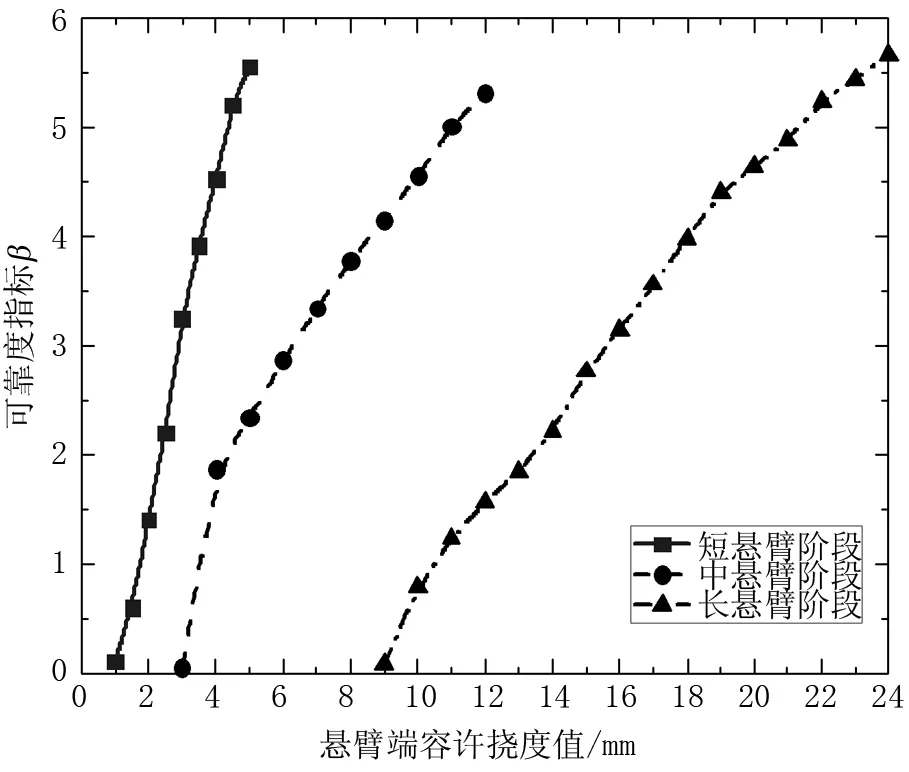
图3 可靠度与容许挠度值关系曲线
综合分析不同悬臂施工阶段的悬臂端容许挠度与结构可靠度指标之间的关系可知,当悬臂端容许挠度越大时,结构对应可靠度指标越高,但悬臂端容许挠度值的增大会导致施工挠度偏差精度控制不高,影响主梁线形,最终导致刚构桥合龙段两端标高偏差较大,不利于刚构桥合龙段施工。因此,为在确保桥梁施工安全的前提下降低主梁线形偏差,取可靠度指标4.0对悬臂端挠度容许值进行控制,此时,由对应曲线关系可知,短、中、长悬臂施工阶段悬臂端最大挠度偏差容许值分别为4、9、19 mm。通过对大跨度刚构桥悬臂施工期间考虑可靠度的悬臂端容许挠度进行分析与控制,指导实际施工,可以有效提升悬臂施工的安全性,提高结构施工阶段可靠度。
4 结 论
(1)极限学习机模型可以较为精确的拟合大跨度预应力钢筋混凝土连续刚构桥随机输入变量与结构挠度响应之间的关系,10个验证集的拟合结果表明,极限学习机响应面模型平均相对误差仅为2.01%,相较于标准SVM具有更高更稳定的拟合精度。
(2)对于短、中、长不同悬臂施工阶段,悬臂端挠度容许值在一定范围内与结构可靠度呈线性相关关系,即在一定挠度容许值区间内,挠度容许值越高,结构可靠度越大,失效概率越低。
(3)为确保大跨度连续刚构桥在保证结构可靠度前提下减小主梁线形挠度,取可靠度指标为4.0对最佳挠度容许值进行分析,根据相关曲线可知,短、中、长悬臂施工阶段最大悬臂端挠度偏差容许值分别为4、9、19 mm。

