山区高低墩梁式桥地震响应特性研究

杜晓菲,吴煜哲

(山东东泰工程咨询有限公司,山东 淄博 256410)

凭借建造便捷、结构简单、成本低廉的优势,连续梁桥在桥梁工程中得到了广泛的应用,成为了较为普遍的桥梁形式之一[1]。需要注意的是,跨度在两跨以上的连续梁桥属于超静定结构,受到外部荷载作用结构内会出现负弯矩区段,这也可以对正弯矩部分产生一定的减缓作用,优化结构受力性能[2]。同时,考虑到负弯矩区段对于正弯矩的分担作用,在设计时能够适当减小主梁高度,以此间接降低结构自重,提升桥梁最大跨度。

在地震作用下,连续梁桥的响应主要表现出以下特点[3-5]。

(1)若设置有固定墩,则在地震作用下桥梁结构所受的地震作用大多由墩体来负担。因此在抗震设计中就需要重点关注固定墩的设计,反复验算其力学性能是否符合要求。

(2)受到水平地震作用,连续梁桥结构的位移以纵桥向和竖向为主,而在横桥向上所发生的位移则相对有限;而对桥墩来说,墩顶位置将发生显著的水平位移,但其竖向位移比较有限。

(3)桥梁墩柱一般具有较大的自重,因此在地震作用下结构内力将沿着支座进一步向下传导至下部结构,因此在抗震设计中还应当重点关注支座强度、变形等,如有必要可在适当位置布置挡块、抗震销。

(4)受到地震作用,矮墩的内力水平一般更为突出。

1 实例工程概况

为了得到地震作用下高低墩连续梁桥结构内所发生的相应,本研究以临淄至临沂段工程连续梁桥模型为基础完成分析。该工程起自沾化至临淄公路,终点位于G20青银高速淄博东枢纽。该桥梁结构采用4×30 m的T型截面设计。对该结构模型分别做纵向、横向以及纵横向高低墩地震响应分析。

根据目标结构建立相应的有限元分析模型:其上部结构通过梁格法来模拟5片首尾相连的T型梁,二期荷载以等效梁单元的形式施加在梁体上,同时将其转变为质量进行定义,将其与梁体自重结合在一块考虑。支座部分通过弹簧单元来近似模拟剪切刚度。此外,盖梁、桥墩、基础等结构均以梁单元完成定义。

为了考虑到桩体在水平方向上的抗力,模拟时选用线弹性地基反力法进行假设,即假定桩侧土体的作用为Winkler离散线性弹簧,且忽略桩间土的摩阻力及粘附力影响,视土体抗拉强度为0,即弹簧仅提供抗压强度而不提供抗拉强度。由此,即可导出土体内任意位置的桩侧土反力及水平位移之间存在正相关性,即

P=k(z)yb0

(1)

式中:P为桩侧土反力,kN;y为桩体水平位移,m;b0为桩体计算宽度,m;k(z)为桩水平变形系数。

2 墩顶抗侧刚度的计算

墩柱顶部抗侧刚度就是使墩顶位置出现单位水平位移时所需附加的相应水平力。考虑到山区地形地势的特殊性,桥梁建设往往伴随产生许多不同形式的高低墩梁式桥。而这一类桥梁往往也具有相同的特点,也即不同桥墩之间的高度差往往比较大,因此墩柱的刚度、自振周期也不尽相同[6]。根据已有的研究[7]可以发现,较等高梁式桥而言,高低墩梁式桥的内力分布存在不均匀、不规则且缺乏规律性的特点。在本节的研究中重点关注墩柱抗侧刚度与结构地震响应之间的关系。

为便于分析,将支座、桥墩视为弹性系数存在差异的两类弹簧,两者间的连接大致简化为串联,桥墩、支座的弹性系数分别定义为K1、K2,桩侧土反力为P,如图1所示。

图1 刚度串联

在对有限元模型进行分析时,在边界条件上设置了挡块的限制,也即定义支座横桥固定,因此在计算分析过程中墩顶位置的抗侧刚度,在K2→∝时,K=K1,即墩顶位置抗侧刚度与墩身抗侧刚度视为等同。为简化分析过程、归纳总结分析规律性,可将桥墩、主梁视为并联连接,因此在桥梁整体刚度时可将各独立桥墩刚度累加,并取各墩柱刚度与桥梁整体刚度的比值。桥墩墩顶抗侧刚度及抗侧刚度比值如图2、图3所示。

图2 不同墩高墩顶抗侧刚度

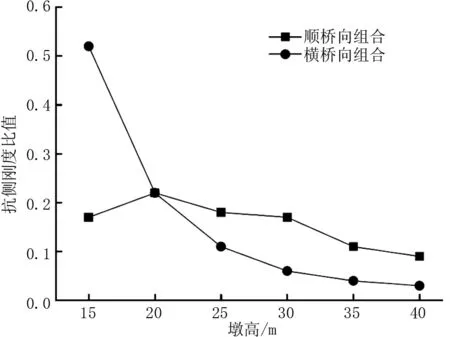
图3 不同墩高墩顶抗侧刚度比

3 墩顶抗侧刚度与墩底内力分布

将墩顶抗侧刚度、墩底截面内力进行比对。在比对过程中,可视桥梁整体所受的地震作用为一个整体,且按照各独立桥墩墩底的地震力累加完成计算,并取各墩底地震力与桥梁整体所受地震力的比值。下面以板式橡胶支座为例,分析研究其在纵桥向定义剪切刚度、横向桥定义固定边界条件的情况下,研究这一比值的变化规律。有限元分析得到墩底位置内力、墩柱抗侧刚度之间的规律,绘制得到规律曲线如图4～图7所示。

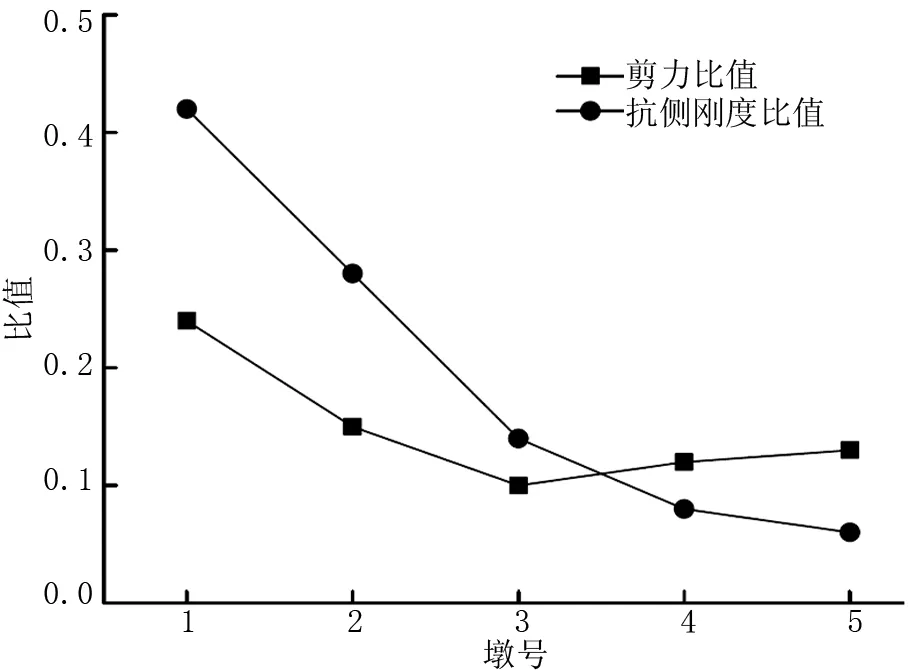
图4 “顺桥向+竖向”地震作用下剪力与抗侧刚度对比情况

图5 “横桥向+竖向”地震作用下剪力与抗侧刚度对比情况

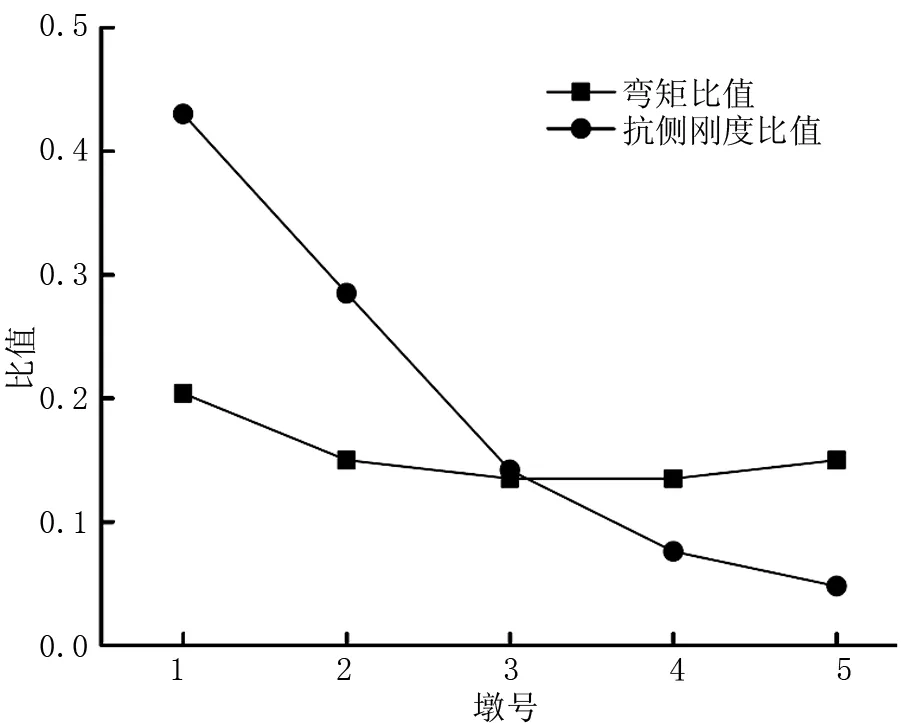
图6 “顺桥向+竖向”地震作用下弯矩与抗侧刚度对比情况

图7 “横桥向+竖向”地震作用下弯矩与抗侧刚度对比情况

(1)剪力与抗侧刚度

(2)弯矩与抗侧刚度

4 横向高低墩地震响应分析

受到地形地势的影响,该项目最终确定建设地在山腰位置的斜坡之上。同时考虑到公路沿线降坡所受的限制,为了方便布设线路按照盘山桥梁的方式进行设计,由此也就导致横桥向的桥墩不可避免地会出现高差。不同于横桥向等高墩桥梁,横向高低墩桥梁存在工程量大、难度高、受力不均匀等缺陷,但其对于复杂地形地势的适应能力更好,设计人员能够采取针对性的灵活设计,所以对其展开研究就显得尤为必要。下面以横桥向高低墩桥梁为对象,探究在地震作用下结构的响应。

分别将横向桥墩的高差取为1～6 m,研究其相应内力变化规律发现,桥墩高差越大,在地震作用下所产生的结构内力也就越大,所以为了提升钢筋布置、调用的便捷性、简化施工内容,就需要尽可能避免桥墩中产生横向高差。若桥墩横桥向高差难以避免,则可通过优化横系梁的方式来进行调整。

对研究数据进行分析可以发现,不同方向的地震作用产生的响应也存在一定差异,其中较横桥向地震作用而言,纵向地震作用的影响更为突出。所以,在设计环节中应当将纵向地震作用下结构的安全性和变形作为重点进行考虑。其次,还需要对横桥向地震作用下的结构做Pushover验算,检验受到地震作用的结构能否满足正常使用要求。

5 横系梁对高低墩桥墩地震响应分析

为了改善桥梁整体刚度,设计人员常常会在大跨度桥梁中适当位置布置连系梁。研究表明[8],对于双柱式桥墩而言连系梁的作用往往较为突出。为了探究连系梁布置数量与结构地震响应之间的关系,并测定桥墩的地震反应谱,本研究假定墩柱高度不变且分别在墩柱间按照五种不同方式布置横系梁。分别为在墩柱底部布置一道横系梁、墩柱底部之上按20 m间距设置两道横系梁、墩柱底部之上按13.3 m间距设置三道横系梁、墩柱底部之上按10 m间距设置四道横系梁、墩柱底部之上按8 m 间距设置五道横系梁。计算分析得到相应的反应谱分别如图8～图10所示。

图8 横向地震作用下墩底及横系梁弯矩

图9 横向地震作用下墩底轴力及剪力

图10 横向地震作用下墩顶位移

有限元分析发现,上述五种连系梁布置方法下墩柱底部所对应的最大弯矩分别为2 271、1 990、1 769、1 597、1 248 kN·m,且其墩柱顶部最大位移分别为32、29、26、21、17 mm。相较于仅在墩柱底部设置一道连系梁,随着连系梁数量的增多,墩柱底部弯矩分别减小了12%、22%、30%及45%,墩柱顶部位移分别减小了15%、24%、39%及51%。由此可以认为,连系梁布置数量的提升对于墩柱底部弯矩、墩柱顶部位移均存在一定的改善效果。

6 结 语

(1)受到“顺桥向+竖向”的组合地震作用,随着墩柱高度的不断提升,墩柱顶部抗侧刚度逐渐下降,墩柱底部剪力逐渐增大,而墩柱底部弯矩则没有显著变化。

(2)受到“横桥向+竖向”的组合地震作用,随着墩柱高度的不断提升,墩柱顶部抗侧刚度逐渐下降,墩柱底部剪力表现为中间小、两侧大的分布,而墩柱底部弯矩则没有显著变化。

(3)对于在墩柱间布置有连系梁的,梁体将成为墩柱底部位置的最不利点,并在该处产生塑性铰,这也能够显著改善桥梁结构的安全性。