高速公路改扩建项目超高设置探讨
叶小宝
(浙江数智交院科技股份有限公司,浙江 杭州 310030)
我国高速公路建设起步得比较较晚,是从20世纪80年代末开始建设的。虽然起步晚,但发展比较迅速,经过了40多年的快速发展,我国高速公路的通车里程已经超过了16万km,高速公路路网已经逐步完善。随着国民经济的高速发展,私家车保有量、社会物流总额逐年增多,高速公路的交通量也迅猛增长。部分高速公路的服务能力已经低于设计服务水平,特别是中东部地区,近年来,改扩建项目已成为高速公路建设的重点工作任务。
由于改扩建工程的特殊性和复杂性,2015年交通运输部专门发布了《高速公路改扩建设计细则》(JTG/T L11—2014),用以规范和指导高速公路改扩建工程的设计。经过几年的使用,发现仍存在一些问题需要解决。比如受地形、地物等条件限制,平面线形不能改变,只能在左右两侧拼宽车道的项目,就存在因车道数变多,超高渐变段相应变长,原有的回旋曲线放不下超高渐变段的问题。
针对此问题,对比分析中国《公路路线设计规范》和美国《A Policy on Geometric Design of Highways and Streets》,提出两种解决问题的方法。
1 改扩建项目超高设计存在的问题
高速公路改扩建项目平面设计一般分为单侧拼宽和两侧拼宽两种类型,平面线形设计受现有桥梁、隧道、互通式立体交叉、分离式立体交叉等结构物以及周边地形、地物等的限制,部分路段只能严格按现有平面线形进行设计,在两侧进行车道拼宽。
由于路面宽度变宽,导致完成的超高渐变段长度变长,原有的回旋曲线长度已经小于超高渐变段长度。如果采用增大回旋曲线长度,改变平面线形的方法,可能会出现占用永农、拆迁困难、原有结构物无法利用等情况,经济成本、环境影响方面都不利。所以如何在回旋曲线不变的情况下,设置变长超高渐变段是需要解决的问题。
2 调整超高渐变段设置位置
2.1 超高过渡段分段分析
将超高过渡段分为两部分,第一部分由完成外车道横坡从路拱坡(-2%)到零坡(0%)的改变所需要道路长度构成,称为克服路拱坡超高过渡段。在克服路拱坡超高过渡段里,由道路横坡产生的横向力Gsinα,方向是向外的,与汽车在曲线上行驶产生的离心力方向一致。此路段里,超高渐变段并没有起到抗离心力的作用,反而增益了离心力。所以克服路拱坡超高过渡段放在曲线里不合适。
第二部分由完成外车道横坡从零坡(0%)到全超高(i%)的改变所需要道路长度构成,称正超高过渡段。在正超高过渡段里,由道路横坡产生的横向力Gsinα,方向是向内的,与汽车在曲线上行驶产生的离心力方向相反。此路段里,超高渐变段起到了抗离心力的作用。
2.2 回旋曲线特点分析
当机动车进入或离开一个圆形的平曲线都会循着一个过渡路径,横向力的方向及大小都会随着变化,并且伴随着横向的位移。对于半径比较大的的曲线,普通驾驶员可以在正常的车道宽度范围内完成过渡路径。但是,在较高行驶速度和较小半径曲线的组合下会导致过渡路径较长,易出现横向位移侵占邻接的车道。在这种情况下,在直线和小半径圆形曲线之间就需要插入过渡曲线,以便驾驶员保持车辆在其自己的行车道内。
驾驶员从直线过渡到圆曲线,如果在开放的平面里进行,它的轨迹将会是一条回旋曲线。所以公路平面设计从直线过渡到圆曲线,就是采用回旋曲线。回旋形过渡曲线模拟车辆的自然转向路径,最小化了侵占相邻车道。回旋曲线提供了天然的、对驾驶员易于行驶的路径,这样车辆进入和离开圆形曲线时横向力的增加和减小逐渐变化。
同时在回旋曲线上进行超高渐变,这样驾驶员转弯很自然,而且还能够抵消逐渐加大的离心力,超高过渡段汽车受力分析见图1。
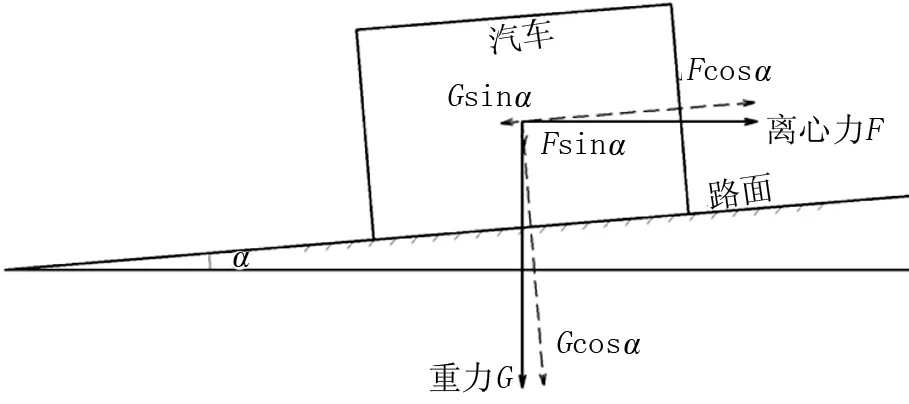
图1 正超高过渡段汽车受力
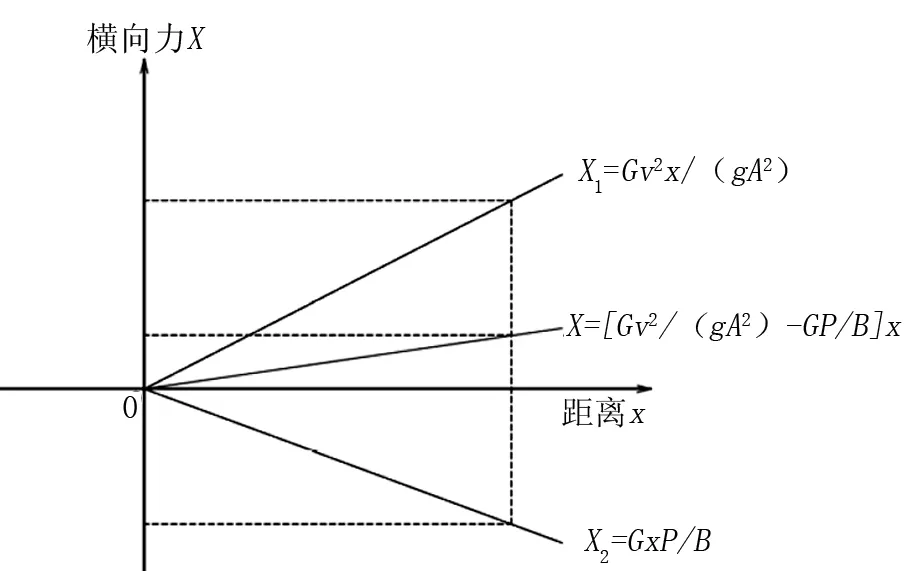
图2 横向力计算示意图
汽车从直线进入回旋曲线后,马上会产生逐渐变大的离心力,可以用公式(1)表示
F=Gv2/(gR)
(1)
式中:F为汽车所受到的离心力,N;G为汽车受到的重力,N;v为汽车的行驶速度,m/s;g为重力加速度,9.81 m/s2;R为圆曲线的半径,m。
根据回旋曲线的特点
R=A2/x
(2)
式中:A为回旋曲线参数,m;x为回旋曲线上任意点到直缓点的距离,m。
离心力产生的横向力X1=Fcosα,因为路拱坡α很小,可设cosα≈1,所以X1=F,再将公式(2)代入公式(1)得到
X1=Gv2x/(gA2)
(3)
由公式(3)可以看出,汽车进入曲线后,离心力产生的横向力X1的大小是随着x从零开始慢慢线性增大的。
2.3 重新设置超高过渡段
如果将整个超高渐变段设置在回旋曲线里,那么在克服路拱坡超高过渡段里,横坡不仅不能帮助抵抗离心力,反而是对离心力是有增益的。
如将克服路拱坡超高过渡段设置在直线段里,把正超高过渡段设置在回旋曲线里,可完美解决此问题。因为在直线段里,不存在离心力,路拱横坡从-2%到0%的变化,不会引起驾驶的不适。
将正超高渐变段设置在回旋曲线里,汽车从直线进入回旋曲线后,会马上产生由横坡产生的抵抗力
X2=Gsinα≈Gtanα
(4)
式中:X2为由正超高产生的抵抗力,N;α为路拱与水平面的夹角,rad。
根据路拱水平夹角和超高渐变率的几何关系可知
tanα=xP/B
(5)
式中:P为超高渐变率;B为超高旋转路面的宽度,m;x为回旋曲线上任意点到直缓点的距离,m。
那么将公式(5)代入公式(4)得到
X2=Gtanα=GxP/B
(6)
由公式(6)可以看出,汽车进入曲线后,由正超高产生的抵抗力X2的大小也是随着x从零开始慢慢线性增大的。
那么由离心力产生的横向力X1和由正超高产生的抵抗力X2的合力X则为
X=X1-X2=[Gv2/(gA2)-GP/B]x
(7)
由此可见,把正超高过渡段放置在回旋曲线上是合适的,此时产生的横向力和超高提供的抵抗横向力是随着回旋线一致变化的。
所以在改扩建项目中,如果平面线形不变,回旋曲线放置不下变长了的超高渐变段时,可以采用将克服路拱坡超高过渡段设置在直线段里,将正超高过渡段设置在回旋曲线里的方法设置超高渐变段。
3 增大超高渐变率,减小超高渐变段长度
3.1 回旋曲线长度分析
回旋曲线最小长度可基于驾驶舒适性和车辆横向移位两方面考虑。基于驾驶员舒适性考虑,目的是提供一个合适长度的回旋曲线,当车辆进入曲线时允许横向加速度缓慢线性得增加。而基于横向偏移考虑,目的是提供一个足够长的回旋曲线,使得车辆在其车道内的横向位移与车辆自然回旋曲线路径产生的位移保持一致。
基于驾驶员舒适性考虑,可参考肖特于1909年为逐步实现铁轨曲线横向加速度而研发的公式,这个公式已被一些公路部门用于计算回旋曲线的最小长度,其表达式见公式(8)。
Lmin=0.0214v3/RC
(8)
式中:Lmin为回旋曲线的最小长度,m;C为横向加速度变化率,m/s3。横向加速度变化率C是经验值,表示回旋曲线提供的舒适性和安全性的水平。0.3 m/s3通常被接受为铁路的操作,公路设计推荐值为1.2 m/s3[1]。
基于横向偏移考虑,可按公式(9)计算回旋曲线的最小长度。
Lmin=(24PminR)0.5
(9)
式中:Pmin为直线和圆曲线之间的最小横向偏移,推荐值为0.20 m,此值与大多数驾驶者因自然转向行为所造成的最小的横向偏移是一致的。
按公式(8)、公式(9)计算得到的回旋曲线的长度,取大值,作为最小回旋曲线长度。有些机构认为回旋曲线的最小长度应为高速公路的设计速度行驶3 s的距离,比如中国和日本就是这么规定的[2]。
但在实际控制回旋曲线长度时,还要考虑设置超高渐变段的长度,而超高渐变段长度很大因素取决于采用的超高渐变率。
3.2 超高渐变率分析
超高渐变率是旋转轴与行车道外侧边缘线之间相对升降的比率,即相对升降高度和超高渐变段长度的比值。最大超高渐变率因设计速度而变化,使得在较高速度时提供更长的超高渐变段长度,在较低速度时提供较短的超高渐变段长度。根据《A Policy on Geometric Design of Highways and Streets》,0.80%和0.35%的相对坡度,分别为20 km/h和130 km/h设计速度提供可接受的超高渐变段长度。按设计速度内插,得到的值见表1。表1的超高渐变率对应的是双向两车道公路绕中线旋转的最大超高渐变率。
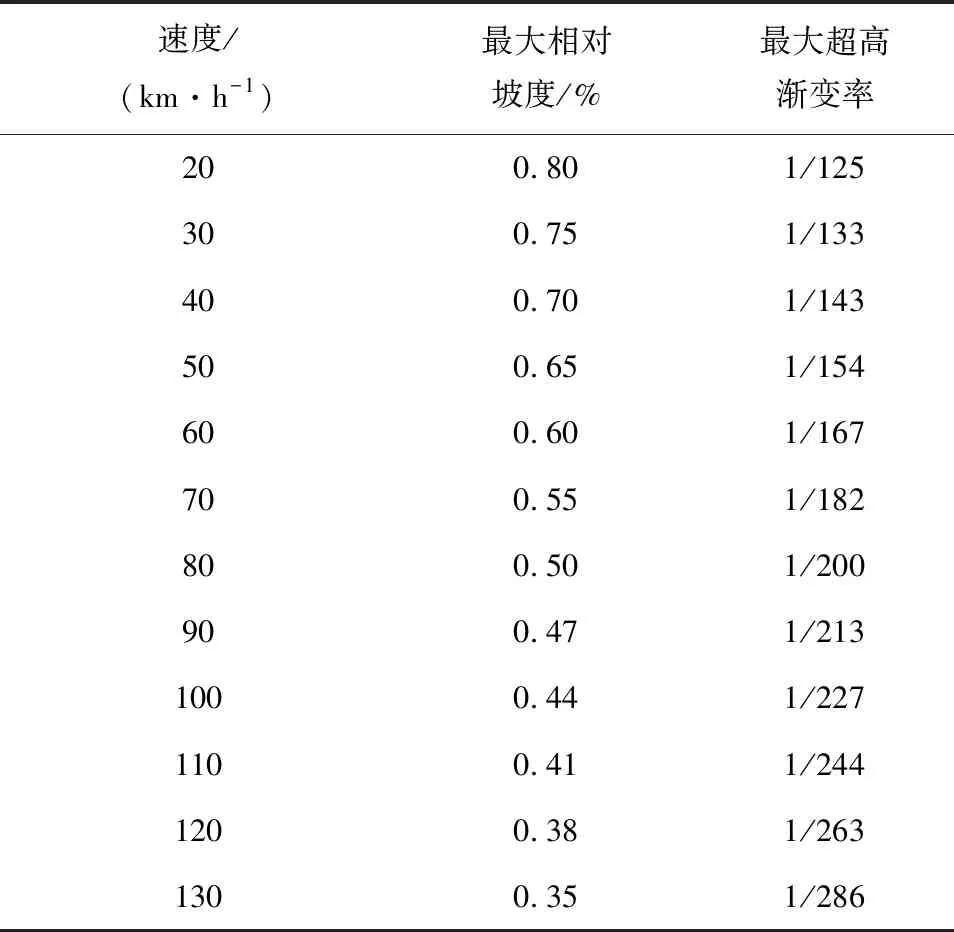
表1 最大超高渐变率表(美国)
旋转车道越多、超高值越大、超高渐变率越小,超高过渡段所需要的长度就越长,超高过渡段长度可按公式(10)计算。
Lc=Δinwf/P
(10)
式中:Lc为超高过渡段长度,m;Δi为超高横坡度与路拱坡度的代数差,%;n为旋转的车道数;w为行车道宽度,m;f为对于旋转车道数调整系数;P为最大超高渐变率。
严格地应用最大超高渐变率计算得出四车道整体式公路的超高渐变段长度是两车道公路的两倍;六车道整体式公路的超高渐变段长度是两车道公路的三倍。虽然这种长度的秩序可能认为是必要的,但在设计中提供这样的长度往往是不实际的,特别是受限于地形等情况,比如改扩建项目。
《A Policy on Geometric Design of Highways and Streets》,基于过往高速公路设计的经验,为避免多车道道路过长的超高渐变段,将最小超高渐变段长度向下调整,推荐的车道数调整系数f列于表2。

表2 车道调整系数表
3.3 与我国设计规范对比分析
我国《公路路线设计规范》对超高渐变率规定了两种情况的超高渐变率[3],见表3。
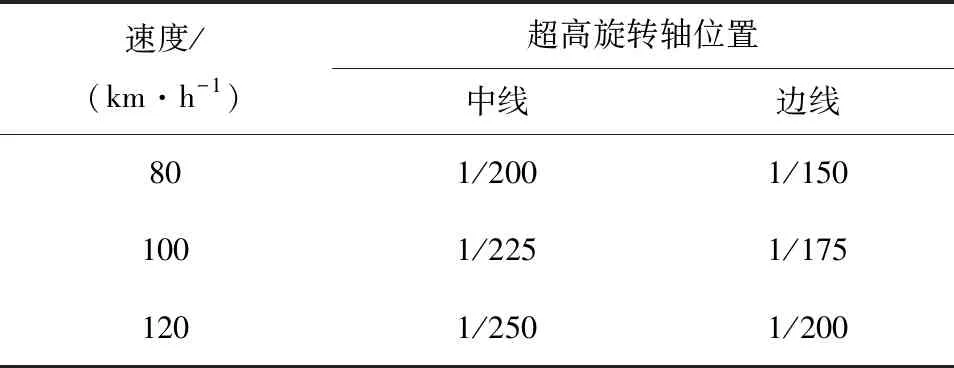
表3 最大超高渐变率表(中国)
与表1对比,发现超高旋转轴位置为中线的超高渐变率与AAHO规定的值基本一致。超高旋转轴位置为边线的,因为比绕中线旋转的车道数变大了一倍,所以计算的时候需要考虑车道调整系数0.75。反映到超高渐变率上,就是绕边线旋转的渐变率应该是绕中线旋转的1/0.75,这与表3中的中线与边线超高渐变率比值基本一致。说明我国编制《公路路线设计规范》是有考虑车道调整系数的。
所以当改扩建公路改扩建的时候,建议放宽超高渐变率的要求,根据表2的车道调整系数,适当增大超高渐变率,以减少超高渐变段的长度。
4 工程案例
斯里兰卡土地是私有制的,公路建设受征地拆迁制约很大,所以平面设计采用的线形指标都较低,特别是回旋曲线长度都较短。中国融资参建的斯里兰卡中部高速公路,设计时速100 km/h,路基宽度24.4 m(中分带2 m,左侧路缘带0.75 m,行车道3.6 m,硬路肩2.5 m,土路肩0.75 m),项目全长36.59 km。
斯里兰卡中部高速与国内改扩建项目的共通点是回旋曲线长度范围内不够设置超高渐变段。项目中半径为1450 m的曲线,采用的回旋曲线长度为75 m,超高从-2.5%渐变到4%。如果将超高渐变段设置在回旋曲线段内,那么超高渐变率P=(0.025+0.04)×(7.2+0.75)/75=1/145>1/225,即使采用车道数调整系数后,1/145仍大于1/225/0.75=1/170的要求。所以采用了将克服路拱坡超高过渡段设置在直线段的方法,则超高渐变率P=0.04×(7.2+0.75)/75=1/235<1/225,符合规范要求。
斯里兰卡中部高速部分路段已通车,首月车流量达50万,车辆运行平稳。所以采用前面论述的两个方法,能有效解决设置超高渐变段困难的问题,国内改扩建项目借鉴采用将起到降低造价、减少耕地占用、减小环境影响等作用。
5 结 论
综上所述,高速公路在改扩建工程,在平面线型不变的情况下,存在原有的回旋曲线不匹配增长的超高渐变段的问题。为此提出将克服路拱坡超高过渡段放置在直线段,将正超高过渡段放置在回旋曲线段,分析了如此设置超高过渡段后,结果显示横向力是沿着回旋线线形变化的,有较好的驾驶舒适性。同时分析了超高渐变段长度和超高渐变率的关系,对比中国规范和美国规范,提出多车道旋转设置超高时应引入车道调整系数,增大超高渐变率,以达到减小超高渐变段长度的目的。通过其中一种方法或者两者结合,解决回旋曲线不够长的问题,降低改扩建项目的投资成本,减小对周边环境的影响。

