基于（1+1）进化策略的港口AGV 路径规划改进进化算法

蒋柳鹏，戴南亭

（河海大学港口海岸与近海工程学院，江苏 南京 210098）

0 引言

AGV（Automated Guided Vehicle），即自动导引车，凭借其智能高效的优势，被广泛应用于港口物流、城市交通和智能仓储系统等领域。港口AGV 路径规划通常指为装运集装箱的AGV 寻找从接货点到卸货点的最优路径。根据AGV 搬运特点，该路径需要综合考虑搬运距离短、避免碰撞、安全转向等问题，以有序完成搬运任务。港口AGV 路径规划是AGV 高效完成货物搬运的核心问题，需要高效的优化算法求解其路径规划模型。

优化算法可分为两大类：一是以数学为基础的经典优化算法，如单纯形法、最速下降法[1]等；二是启发式智能优化算法，如遗传算法、模拟退火算法、差分进化算法等。经典优化算法计算复杂，无法求解高维度、复杂目标函数的问题，因此AGV 路径规划中更多采用智能优化算法。其中进化算法（evolutionary algorithms，EA）是智能算法中的一个重要的“算法簇”，其产生的灵感源于大自然中生物的进化[2]。与基于微积分的传统方法和穷举法等优化算法相比，进化算法更加成熟，且作为全局优化方法具有鲁棒性高、适用性广及自组织、自适应和自学习的特性，能够有效处理传统优化算法难以求解的复杂问题，所以AGV 路径规划问题可以用EA 算法求解。

进化算法主要有3 种类型：遗传算法（genetic algorithm，GA），进化规划（evolutionaryprogramming，EP）和进化策略（evolutionary strategies，ES）等[3]。其中ES 摒弃了梯度计算，强调个体级的行为变化，使用交叉算子，采用实数值作为基因，并且遵循零均值、某一方差高斯分布的变化产生新个体，在选择和变异的操作上更为灵活，整体计算更加高效，适用于AGV 路径规划问题。

根据选择方法的不同，进化策略可以分为（1+1）进化策略（（1+1）-ES）和（μ，λ）进化策略（（μ，λ）-ES）两种，其中（1+1）-ES 较为方便有效，被广泛应用。近年国内外学者针对（1+1）-ES 算法的改进做了大量研究，KAYHANI A 等[4-5]引入步长自适应机制，并应用于基准函数和工程实例，结果表明，与其他算法相比，该算法具有高效性、鲁棒性和全局寻优能力；KRAMER O 等[6-7]提出一种可以自适应改变算法中学习参数的方法，实验结果表明该算法的总体性能有了显著提高；JEBALIA M 等[8-9]基于（1+1）-ES 对球函数上的收敛性进行了数学分析，并显著提高其边界下限，实现了对均匀突变算子的连续优化。

在AGV 路径优化问题上，目前使用较多的有强化学习、A*算法、Dijkstra 算法、蚁群算法和遗传算法等[10-14]，（1+1）-ES 算法在AGV 路径规划中的研究成果较少。因此，本文尝试提出一种改进的（1+1）进化策略及相应算法，应用于AGV 路径规划问题，同时优化该问题的适应度函数，以提升AGV 路径规划的效果。

1 AGV 路径规划问题

1.1 AGV 路径规划环境建模

AGV 在港口码头进行搬运工作的实际环境如图1 所示，集装箱被AGV 从堆场运至岸桥进行装卸，实际环境由AGV、障碍物和支路组成。为方便研究，将AGV 假设成一个质点，将作业区的障碍物假设为同一尺寸，不考虑其实际尺寸。基于栅格地图法操作较为简单、易于理解和实现的优点，本文采用栅格地图法进行环境建模，长为3个单位栅格长度、宽为1 个单位栅格长度的黑色栅格表示障碍物，空白栅格表示可自由移动的空间，地图左下角的黑色栅格表示AGV 运动的起点，地图右上角的黑色栅格表示AGV 运动的终点[15]，AGV 环境建模如图1 所示。

图1 AGV 工作环境实际地图和建模地图Fig.1 Actual map and modeling map of AGV working environment

将AGV 工作环境等分为20 行20 列的栅格地图，单位栅格可完全容纳AGV，地图上的所有点都可用坐标表示。控制系统通过后台控制向AGV发送搬运任务，AGV 会沿着计算得出的路径进行运动，将该路径上的点用栅格中的坐标表示，这些坐标通过遗传算法的编码后变成一条路径染色体，每一条染色体便代表了一个解即一条路径。

1.2 AGV 路径规划适应度函数设计

适应度函数是筛选路径的标准，用来评价路径的优劣，适应度越高说明该路径越符合设定的约束条件[16]。传统路径规划的适应度函数大多采用路径长度最小为目标函数，本文结合港口码头AGV 实际的工作情况，例如AGV 运行过程中可能存在转弯和与障碍物碰撞的情况，若转弯角度过大或与障碍物碰撞将降低搬运的工作效率，并造成AGV 的损坏，所以本文对目标函数进行了改进，在路径长度的基础上增加了路径平滑度和碰撞风险函数，从路径长度、路径平滑度、碰撞风险这3 个方面设计港口码头AGV 路径规划的适应度函数。

1） 路径长度

（xi，yi）表示地图上第i个点的坐标，Li表示（xi，yi）和（xi-1，yi-1）两点之间的距离，相邻两点间的距离公式如下：

总的路径长度公式如下：

将L无量纲化，并设置目标函数为：

2） 路径平滑度

在AGV 运行过程中需要转弯时，若转弯角度过大将增加AGV 通过的时间，降低工作效率，并对AGV 本身造成一定的损耗，所以本文对路径平滑度函数设置惩罚系数ω。当转弯角度θ<45°时，ω 设置为1；当转弯角度45°≤θ≤90°时，ω 设置为10；当转弯角度θ>90°时，ω 设置为1 000。将ωθ 无量纲化，并设置路径平滑度函数如下：

3） AGV 与障碍物碰撞风险

当障碍物的位置与AGV 的位置越近时，AGV与障碍物的碰撞风险越高，为防止AGV 与障碍物发生碰撞，本文设置位置风险系数λ。本文选择将距离AGV 最近的障碍物的中心点坐标（xj，yj）与AGV 的位置坐标（xi，yi）间的距离作为判断标准，若距离小于1.5 个单位栅格长度则判断为有较大的碰撞风险，λ 设置为100，反之则λ=0。将λLij无量纲化，并设置障碍物与AGV 间的距离和碰撞风险函数如下：

综合上述因素，设计路径评价函数为：

式中：a、b、c为权重系数，且三者和为1。

当路径评价函数数值越大时，说明该个体适应度越高，被保留到下一代的概率越大；当路径评价函数数值越小时，说明该个体适应度越低，被保留到下一代的概率越小，该染色体被淘汰的概率越大。

2 （1+1）-ES 的AGV 路径规划求解算法设计

（1+1）-ES 是进化策略中较为简单有效的一种[17]，是1 个父代通过高斯变异产生1 个子代寻优的算法，即只有1 个父亲且每次只产生1 个新的个体，然后从这2 个个体中保留较好的进入后续的进化[18]。为了能够在AGV 路径规划巨大的解空间中探索更好的解，避免陷入局部最优的情况，需要对变异过程进行改进，（1+1）-ES 是较好的方法。

（1+1）-ES 的变异强度由正态分布N（0，δ）决定，δ 为变异强度，通过控制分布，选取扰动，用扰动影响进化强度；通过对比扰动带来的反馈，选择成功变异的扰动，控制进化方向，能否找到最优解很大程度上取决于δ[19]。（1+1）-ES 的收敛过程遵循1/5 成功原则，当个体中有1/5 的变异个体比原始个体优秀时即判断为即将收敛。收敛过程中如若未达到收敛条件，则增大变异强度，如若即将达到收敛条件，则减小变异强度。该策略根据历史成功变异能力不断调控δ，在很大程度上解决了使用其他优化算法会出现的陷入局部最优的问题。本文提出的（1+1）-ES 算法流程图见图2。

图2 （1+1）-ES 算法流程图Fig.2 (1+1)-ES algorithm flowchart

该算法过程如下：

1） 通过样本产生初始个体x；

2） 通过初始个体x和变异强度δ 产生新的解，公式如下：

3） 计算个体的适应度函数值f（x）和f（y），如果f（y）>f（x），则用y替换x；

4） 调控变异强度大小，重复操作2） 和3）直到满足输出条件后输出结果，变异强度的公式如下（δɡ表示第ɡ 代个体的变异强度，ps表示变异成功率，Cd为固定参数）[20]：

本文提出的（1+1）-ES 算法在原（1+1）-ES 算法基础上改进了其适应度函数，提高了适应度函数的综合程度，使其更适用于本文要解决的AGV路径规划问题。

3 仿真实验

本文使用的路径规划算法在Python 语言和spyder 平台进行开发，相关软件及第三方库的版本如下：Python 3.8.5，geatpy2.6.0。程序调试和算例求解均在1 台CPU 主频为1.80 GHz，GPU 为NVIDIA GeForce MX150，内存为8.00 GB 的个人计算机上完成。

3.1 AGV 静态路径规划仿真实验

在AGV 静态路径规划中只考虑所有障碍物都是静止状态的情况，即地图中不存在动态障碍。地图中静态障碍物的尺寸皆设置为长3 个单位栅格长度、宽1 个单位栅格长度，AGV 由1 个单位栅格表示，AGV 的仿真任务为从起点运行到终点。起点和终点也由1 个单位栅格表示，起点的坐标为（0，0），终点的坐标为（20，20）。其他各参数设置见表1。

表1 参数设置信息Table 1 Parameter setting information

使用本文设计的（1+1）-ES 算法得到的部分最优路径见图3，路径具体信息见表2。

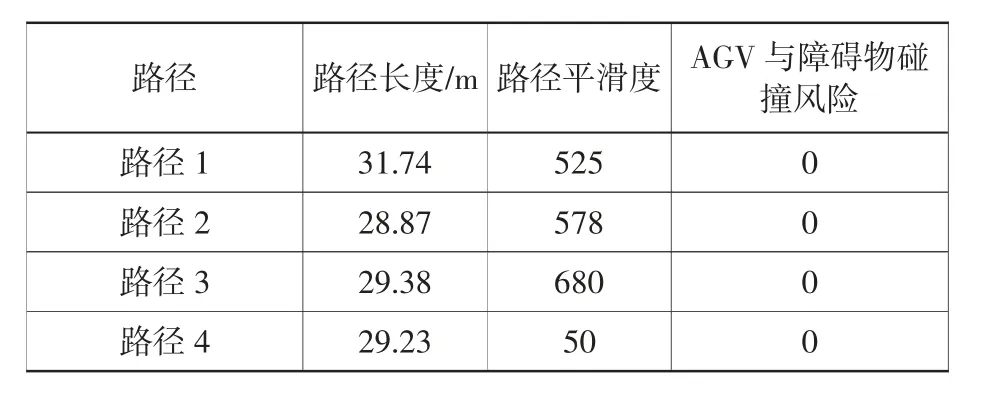
表2 基于（1+1）-ES 的部分路径具体信息表Table Partial path specific information based on(1+1)-ES

图3 基于（1+1）-ES 的AGV 静态路径规划图Fig.3 Static path diagram of AGV based on(1+1)-ES

由图3 和表2 可以看出，使用本文提出的基于（1+1）-ES 的AGV 静态路径规划得到的路径在地图中分布较广，没有出现大部分路径高度重合的情况，即算法在整个过程中没有出现陷入局部最优的情况，搜索范围较为广泛。这4 条路径虽然都被算法的适应度评价指标评价为最优路径，具体路线不同，但这些路径的优势各不相同。路径1 开始所行方向与终点相差较远，所以路径长度是4 条路径里最长的，转弯次数较少且角度较小所以路径平滑度较为优秀；路径2 的路径长度最小，但由于AGV 三次转弯的角度都偏大，所以路径平滑度相对较差；路径3 由于转弯次数较多且转弯角度较大，所以路径平滑度是4 条路径里最大的，但总体运行方向相比于其他3 条路径最为接近起点与终点的直线，所以路径长度较短；路径4 的转弯角度较小，所以路径4 的路径平滑度最小即转弯角度总和最小，转弯次数较少，所以路径长度也较小。总体来说这4 条路径的2 种指标都较为优秀，且所有路径的碰撞风险皆为0。

由上述仿真实验结果可以看出：在静态的环境下，使用本文设计的基于（1+1）-ES 的方法可以实现较为优秀的路径规划，该算法对各项指标都能够有一定程度上的优化，很大程度上避免了其他算法可能出现的陷入局部最优的问题。

3.2 AGV 动态路径规划仿真实验

考虑到AGV 的实际工作场地除了静态障碍物外，会有工作人员随机出现的情况，在原始的地图上增加5 个随机生成的栅格来代表可能会出现的工作人员。静态障碍物的尺寸设置和向AGV 发布的模拟任务同静态路径规划相同，算法的各参数设置也相同，具体参数设置见表2。为更加直观地看出本文设计的基于（1+1）-ES 的优势所在，本文选择将其结果与差分进化算法和遗传算法所得结果进行对比分析。3 种算法皆使用同样的参数和栅格地图，其中遗传算法的变异概率设置为0.8，交叉概率设置为0.6，得到的某一条最优路径如图4 所示，路径信息如表3 所示，算法收敛如图5 所示。路径平滑度较大，路径长度也较长，这会降低AGV 的工作效率和增加对AGV 的损耗，另外未考虑碰撞的风险；由差分进化算法得到的最优DE 算法路径在运行过程中同样出现多次转弯角度过大的情况导致该条路径的路径平滑度较大，路径长度较长，并且在运行过程中有一处与障碍物相距过近，增加了AGV 与障碍物碰撞的风险；由（1+1）-ES 得到的最优（1+1）-ES 算法路径运行方向总体与起点和终点间的连线最为接近，所以路径长度相较于其他2 条路径最短，并且转弯次数较少，所有转弯角度皆小于45°，所以路径平滑度最小，无碰撞风险。

表3 基于不同算法的部分路径的具体信息表Table 3 Partial path specific information based on different algorithms

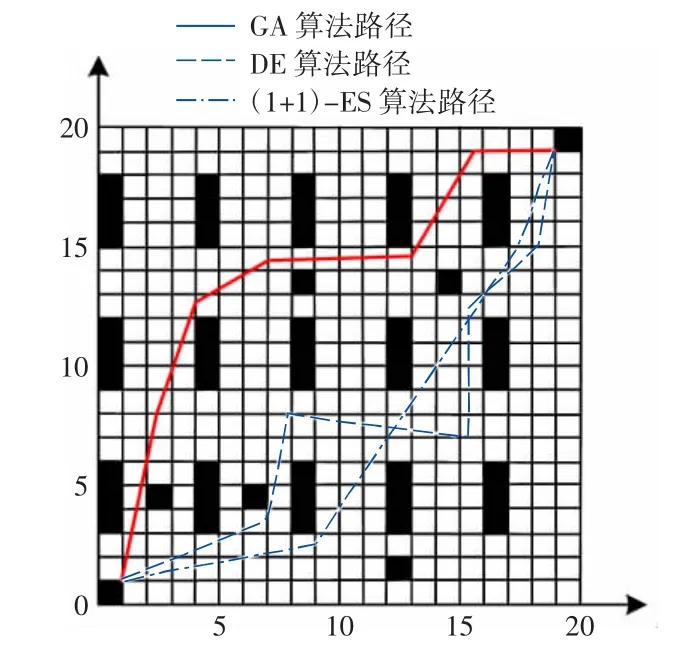
图4 3 种不同算法的AGV 动态路径规划图Fig. 4 AGV dynamic path diagram with three different algorithms

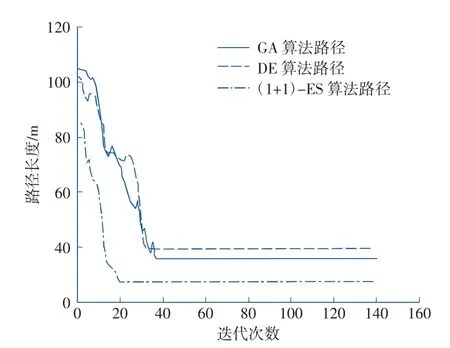
图5 算法收敛曲线Fig.5 Algorithmic convergence curve

由图5 可以看出，遗传算法的算法收敛曲线在迭代次数为0~38 次之间波动较大，运行不稳定，在迭代38 次时达到收敛状态；差分进化算法的收敛曲线在迭代次数为0~36 次之间波动较大，运行同样不够稳定，在迭代36 次时达到收敛状态；（1+1）-ES 前期有一处波动，总体运行较为稳定，且收敛速度相比于其他2 种算法更快，在迭代20 次时达到收敛状态。

综合分析，可以看出本文设计的（1+1）-ES 在适应度指标、运行稳定和收敛速度这3 个方面都明显优于遗传算法和差分进化算法，优势总结具体见表4。

表4 不同算法结果的对比Table 4 Comparison results of different algorithm results

由图4 和表3 可以明显看出，在设置同样的参数和地图条件下，本文设计的（1+1）-ES 算法在路径长度和路径平滑度上明显优于遗传算法和差分进化算法。由遗传算法得到的最优GA 算法路径在运行过程中多次出现转弯角度过大的情况，其中1 个转弯的角度超过了90°，导致该条路径的

4 结语

本文提出了一种基于（1+1）-ES 的AGV 路径规划改进算法，从路径长度、路径平滑度和碰撞风险3 个方面改进了算法的适应度函数，使其更加适用于AGV 的路径规划问题。

在仿真实验中设计栅格地图来模拟实际港口AGV 的工作环境，通过仿真实验可以看出，在静态路径规划和动态路径规划中，本文提出的改进后的（1+1）-ES 算法均提高了搜索效率，并有效解决了算法求解易陷入局部最优的问题，验证了本文提出的基于（1+1）-ES 在解决AGV 路径规划中的高效性和可靠性。

本文在有限障碍物和单个AGV 的前提下进行了路径规划研究，在后续的研究中，本文将对障碍物的随机性和不确定性进行进一步的复杂假设，并且加入其它的AGV 进行多AGV 的路径规划问题研究。