基于强化学习的城市场景多目标生态驾驶策略*
李 捷,吴晓东,许 敏,刘永刚
(1.上海交通大学机械与动力工程学院,上海 200240;2.重庆大学,机械传动国家重点实验室,重庆 400044)
前言
为提高电动汽车(electric vehicle,EV)的经济性,除开发更先进的高效“三电”系统,改善车辆行驶行为以提高车辆经济性的生态驾驶技术也受到了广泛关注。传统的生态驾驶策略是指驾驶员经过科学培训习得的通过控制车辆行驶速度降低油耗的驾驶技能[1]。随着智能网联汽车(connected and automated vehicle,CAV)技术的发展,车辆可以通过V2X(vehicle-to-everything)通信接收周围交通和道路地形信息[2]。CAV 不仅可以降低能源消耗,还可以给乘客提供良好的乘坐体验(如保障驾驶安全,提高舒适性和通行效率)。因此,开发多目标生态驾驶策略来优化CAV的行驶行为是目前的研究热点[3-4]。
已有的生态驾驶策略主要分为基于规则、基于优化和基于学习的3 类。典型的基于规则的生态驾驶策略是“脉冲-滑翔”策略[5-6]。理想情况下,该策略控制车辆匀加速至给定速度,然后保持匀速运行,最后匀减速运动至目的地,从而达到节省燃料消耗的目的。然而,在真实驾驶场景中,由于红绿灯路口的隔断以及其他车辆不确定行为的干扰(例如换道、超车、急停等),自车难以按照理想车速轨迹行驶。尽管该策略具有较好的实时性,但过度简化了交通环境,没有考虑交通环境中的复杂影响因素,难以在城市场景中实际应用。
基于优化的生态驾驶策略通常将生态驾驶问题建模为最优控制问题,然后通过动态规划[7]、非线性规划[8]、模型预测控制[9-10](model predictive control,MPC)等方法求解。然而,基于优化的生态驾驶策略需要建立一个能反映复杂的车辆动力系统与多变的城市交通环境特性的非线性模型。而该模型也必然包含多个状态变量。虽然通过对车辆动力系统与交通环境进行精确建模能保证算法的优化效果,但是求解含有复杂非线性模型的最优控制问题需要消耗大量的计算资源,难以在算力有限的车载控制器(vehicle control unit,VCU)中实时应用。
深度强化学习(deep reinforcement learning,DRL)算法是一种基于数据驱动的机器学习方法,它不需要建立复杂的动力学控制模型,而是仅通过智能体(agent)与环境的交互来学习和优化控制策略。训练好的DRL 智能体可以通过深度神经网络(deep neural network,DNN)接收系统状态信息,并快速计算出对应的控制动作[11]。相比于基于模型的优化控制方法,避免了对复杂动力学控制模型的依赖,可以有效降低控制策略的计算量,实现实时控制[12]。然而,DRL 算法在基于学习的生态驾驶策略上的应用仍存在着多种挑战。与传统RL算法相比,DRL算法依靠DNN 来近似最优值函数[13],避免了算法在多个状态变量的复杂场景中陷入“维数灾难”。但是,由于函数近似误差的存在,DRL 算法也不可避免地引入了控制不稳定性[14]。因此,仅依赖于DRL 算法的生态驾驶策略难以在实际应用中充分保障车速规划的安全性。此外,复杂交通场景下多目标生态驾驶问题的奖励函数设计是一个棘手的问题,直接关系到DRL 算法训练能否收敛。奖励函数应能恰当地定义生态驾驶问题的优化目标,并准确地反映交通灯、前车、道路限速等交通影响因素。为了降低算法训练收敛的难度,目前基于DRL 的生态驾驶策略的研究大都考虑单一的交通影响因素,与实际交通场景存在较大差异。
例如,Liu等[15]提出基于深度确定性策略梯度法的生态驾驶策略,可以快速求解多个信号灯路口之间的最优车速轨迹。然而该DRL 控制器没有考虑安全跟车约束,只适用于单车行驶的理想状况。Bai等[16]提出了一种结合安全决策规则与DRL 的混合生态驾驶策略框架,以改善复杂交通路口的车辆能源效率。然而该混合框架只通过决策管理器选择传统规则策略或DRL 策略控制车辆,并未把安全约束融入DRL 算法的设计中。张健等[17]提出一种基于离线DRL 的车辆交叉口生态驾驶控制策略,实现了能耗经济性的提高。然而该方案忽略了DRL 算法控制不稳定所带来的安全问题而且也未考虑跟车场景。
为了克服当前研究的不足,本文提出了一种新型基于DRL 的实时多目标生态驾驶策略,以有效应对复杂交通场景下的驾驶挑战。本研究的贡献如下:针对DRL 算法控制稳定性不足的问题,设计了面向实际应用的基于DRL 的生态驾驶策略的框架,通过安全速度建议模块实现了对车速规划的安全性保障;而为了使DRL 算法考虑多个交通影响因素并促进该多目标生态驾驶策略训练收敛,提出了一种融合安全约束与塑形函数的多目标复合奖励函数设计方案。最后,通过硬件在环(hardware-in-loop,HIL)实验验证了所提控制算法在真实的VCU 中实时应用的有效性。
1 问题描述
1.1 智能网联汽车动力系统结构
本文的研究对象为一款基于纯电动平台的CAV。电机、主减速器和差速器依次组装在该车的动力系统中。电机输出转矩与车辆加速度之间的关系可以表示为
式中:Ftra、τm、ifd、ηfd、ηdif与rwheel分别为车轮驱动力、电机转矩、主减速比、主减速器效率、差速器效率与车轮半径;aego、m、g、fr、α、CD、A、ρ、vego和Iequi分别为车辆加速度、车辆质量、重力加速度、滚动阻力系数、道路坡度、空气阻力系数、迎风面积、空气密度、自车车速与旋转部件在车轮处的等效转动惯量。针对纯电动CAV 而言,控制策略通过控制电机输出的驱动转矩来调节车辆加速度,从而控制车辆实现目标车速。合理规划车辆的行驶速度可以改善车辆的乘坐体验。
1.2 智能网联场景下的生态驾驶问题
如图1 所示,当车辆在城市交通场景中行驶时,必须考虑前方红绿灯路口、道路坡度、道路限速、前方车辆等多种交通要素的约束。
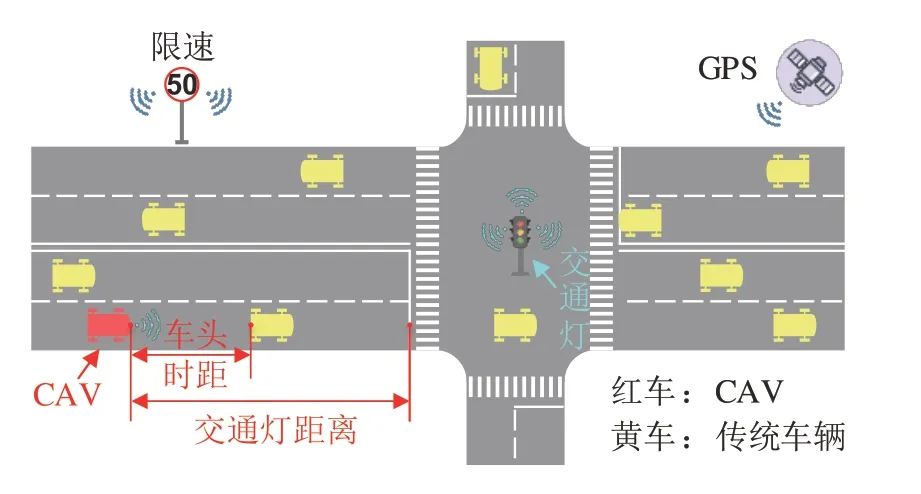
图1 智能网联场景示意图
在智能网联场景中,由于CAV 可以通过车载传感器与V2X 通信获取实时交通环境信息(例如:前车距离/车速信息、红绿灯时间/相位信息、道路限速信息等)。因此,在智能网联场景下,多目标生态驾驶问题可以表述为:利用获取的交通环境信息,合理规划CAV 的目标车速,并在满足安全约束(遵守交通规则,避免碰撞)的前提下,实现电力消耗、乘坐舒适性和出行效率的协同优化。
式中:α1、α2与α3为各指标的权重系数;N、Pbat和ΔT分别为行程长度、电池功率和单位控制步长;Nred_light、Ncollision与vlimit分别为闯红灯次数、碰撞次数与道路限速。
由于目前CAV 在实际道路上的渗透率较低,因此在研究场景中,假设其他车辆均为传统的人工驾驶车辆。此外,为了简化问题,本文只考虑影响自车纵向运动的相关因素,例如速度、加速度、交通信号灯和前车等,而不考虑车辆的横向动作。
2 基于深度强化学习的生态驾驶策略
为了解决上述多目标生态驾驶问题,本文提出了一种基于DRL 的实时生态驾驶策略,策略框架如图2 所示。DRL 算法根据收到的交通状态与自车状态信息,利用训练好的DNN 计算车辆目标参考车速。同时,基于跟车安全模型与交通灯安全模型的安全速度建议模块用于实时监控并修改DRL 智能体规划的高风险动作,以保障驾驶安全。修改后的参考速度被发送给底层动力系统中的车速跟踪控制器。然后,由车速跟踪控制器利用参考车速与实际车速的误差计算驱动电机输出转矩,以控制车辆跟踪参考车速。所提生态驾驶策略的设计与实现细节详细介绍如下。

图2 基于深度强化学习的生态驾驶策略框架
2.1 基于马尔可夫决策过程的生态驾驶问题
DRL方法通常将实际环境简化为马尔可夫决策过程(Markov decision process,MDP)[11]。即假设环境转移到下一个状态si+1的概率仅与上一个状态si有关,与更早之前的状态无关。在状态si执行动作ai后,转移到状态si+1的概率可以定义为
式中:s′为下一个状态;s和a为当前i时刻的状态与动作。DRL 的动作可以由策略π决定。当策略π是确定策略时,当前状态si下采取动作ai后的期望累积收益可以推导为
式中:期望累积奖励Qπ(si,ai)也被称为动作价值(或Q 值);γ∈[0,1]为折扣因子;T为有限MDP 的长度;rn(sn,an)为在状态sn采取动作an后的奖励值;E为状态集合。对于MDP,式(5)可以转化为如下递归关系:
DRL 算法的任务是找到一个最优的策略π*,使期望的累积奖励Qπ(si,ai)最大化。对于本文研究的多目标生态驾驶问题而言,式(3)的目标函数也可被表述为递归形式:
式中:costins(i)表示考虑电耗、舒适性与行驶效率的瞬时成本。比较式(6)与式(7)可知,当DRL 的奖励函数等于负的瞬时成本时,生态驾驶问题的目标函数可以转化为基于MDP的DRL算法的价值函数。
式中:rele=-Pbat为电耗奖励;rcon=-|aego|为舒适度奖励;reff=-ΔT为通行效率奖励。通过与环境交互,DRL 智能体可以迭代更新得到使累积奖励函数Qπ(si,ai)最大化的最优策略π。该最优策略可以直接应用于车辆生态驾驶控制,实现车辆电耗、舒适性和出行效率的协同优化。
2.2 状态空间与动作空间设计
如前文所述,生态驾驶策略需要在满足安全出行的前提下,实现经济性、舒适性和出行效率的协同优化。因此DRL 智能体的输入信息应充分反映车辆动力系统状态和交通环境状态。本研究中,DRL智能体的状态输入由如下3部分组成。
(1)车辆状态信息:参考车速vref、实际车速vego、电池SOC、电池内阻Rbat、电池开路电压Ubat。
(2)前车信息:前车速度vpre、前车加速度apre、两车距离dhead。
(3)道路信息和交通灯信息:自车行驶距离dego、道路坡度α、下一个交通灯路口距离dlight、交通灯剩余时间trem、交通灯相位。
在本文中交通灯剩余时间和交通灯相位被交通灯时间tlight所代替。它可以在降低输入状态维数的同时不丢失交通灯时间/相位信息。
式中Tred为红灯相位持续时间(注:在本文中,黄灯相位也被纳入红灯总时间中)。根据上述分析,观测状态向量公式如下:
为了合理控制车辆速度变化,本文选取车辆加速度作为DRL 智能体的动作变量输出。故DRL 智能体给出的自车参考速度可表示为
式中aDRL为DRL算法计算的车辆加速度。车辆加速度被限制为以避免产生不舒适的急加速/减速动作。
2.3 安全速度建议模块设计
安全速度建议模块由跟车安全模型和红绿灯安全模型组成。
2.3.1 跟车安全模型
为避免与前车发生碰撞,车速上限表示为
式中vKrauss是基于Krauss 跟车模型[18-19]推导的最大安全跟车速度。
式中:amax是最大加速度;Δdhead=dhead-Dmin;Dmin与τ分别为最小车头距与驾驶员反应时间。通过引入驾驶员反应时间,使得DRL 智能体可以学习类似于人类驾驶员的反应过程,从而提高乘客的接受度。
2.3.2 交通灯安全模型
如果车辆无法在绿色时间内通过交通路口,则车辆应及时停车避免闯红灯。因此,最大安全速度可表示为
此外,本文还根据红绿灯剩余时间tremain与离红绿灯距离dlight定义了一个阈值速度vtho(i)。
当车辆处于交通灯区域且交通灯为绿色时,避免闯红灯的安全参考速度上限可以表示为
当车辆处于交通灯区域且交通灯相位为黄色或红色时,避免闯红灯的安全参考速度上限可以表示为
根据式(12)、式(16)与式(17),基于跟车安全模型与交通灯安全模型的速度建议模块计算的安全速度上限可以表示为
式中δcf与δtl为调整速度建议模块安全阈值的比例因子。
此外,为了避免DRL 智能体规划负参考车速的不合理情况,本文采用安全速度建议模块进行修正。具体而言,当式(11)计算得出参考车速小于0 时,安全速度建议模块将把输出的安全参考车速设置为0。
因此,经过速度建议模块对DRL 智能体规划的高风险参考速度进行监控与修改后,发送给车速跟踪控制器的安全参考车速可以表示为
2.4 融合安全约束与塑形函数的奖励函数设计
为了使DRL 智能体学习一种既能满足安全约束又能实现多目标协同优化的生态驾驶策略,本研究除了式(8)基于目标函数转化的基础多目标奖励函数之外,还设计了式(20)安全约束奖励。
式中:α4为权重系数;aref(i)为速度建议模块修改后的加速度。
通过添加安全约束奖励函数,将安全约束条件融入模型训练中,可以使DRL 智能体在优化行驶车速时,避免输出会导致速度建议模块介入的高风险动作。
此外,在复杂交通场景中,多目标DRL 智能体的训练难度较大[16]。为了克服这一问题,本文设计了一种可以提供先验知识的塑形奖励函数,以鼓励DRL智能体产生安全高效的驾驶行为。该塑形奖励函数根据基于势能的塑形函数设计理论[20-21]开发,以确保添加塑形奖励函数后的最优策略不变性。
式中:Ffollow、Flight与Feff分别为跟车塑形奖励、交通灯塑形奖励与通行效率塑形奖励;γ∈[0,1]为折扣因子;Φfollow、Φlight与Φeff分别为跟车势函数、交通灯势函数和通行效率势函数。如果势函数的值较高,则表示当前环境所处状态接近所期望的状态。而当环境状态偏离期望状态时,势函数的值会减小。本文中势函数设计如下:
式中vadvisor(i)为根据交通灯时间/相位信息以及到交通灯距离信息计算的绿灯通行建议速度。
式中:n∈(0,1)为调节建议速度大小的权重;vlg_min与vlg_max为绿灯通行速度区间,计算方法如下。
如图3所示,根据dlight与下一个绿色相位的起止时间可以计算出车辆在此绿色相位内匀速通过路口的速度区间[vlg_min,vlg_max]。如果在道路限速内无法通过路口,则选择下一个周期的绿色相位作为目标相位重新计算[vlg_min,vlg_max]。
因此DRL智能体的总奖励函数为
2.5 基于TD3的参考速度规划算法实现
由于算法的状态与动作变量都是连续变量,因此本文选择适用于连续状态与动作空间的双延迟深度确定性策略梯度法(twin delayed deep deterministic policy gradient,TD3)来实现基于DRL的生态驾驶策略。基于TD3的生态驾驶智能体如图4所示,包含一个Actor神经网络μ(s|θμ)和两个Critic神经网络其中与为网络各节点的权重与偏置参数。TD3算法是目前最先进的用于连续控制的DRL 算法之一,通过设计两个Critic网络减小了Critic网络对动作价值函数的近似误差[14]。
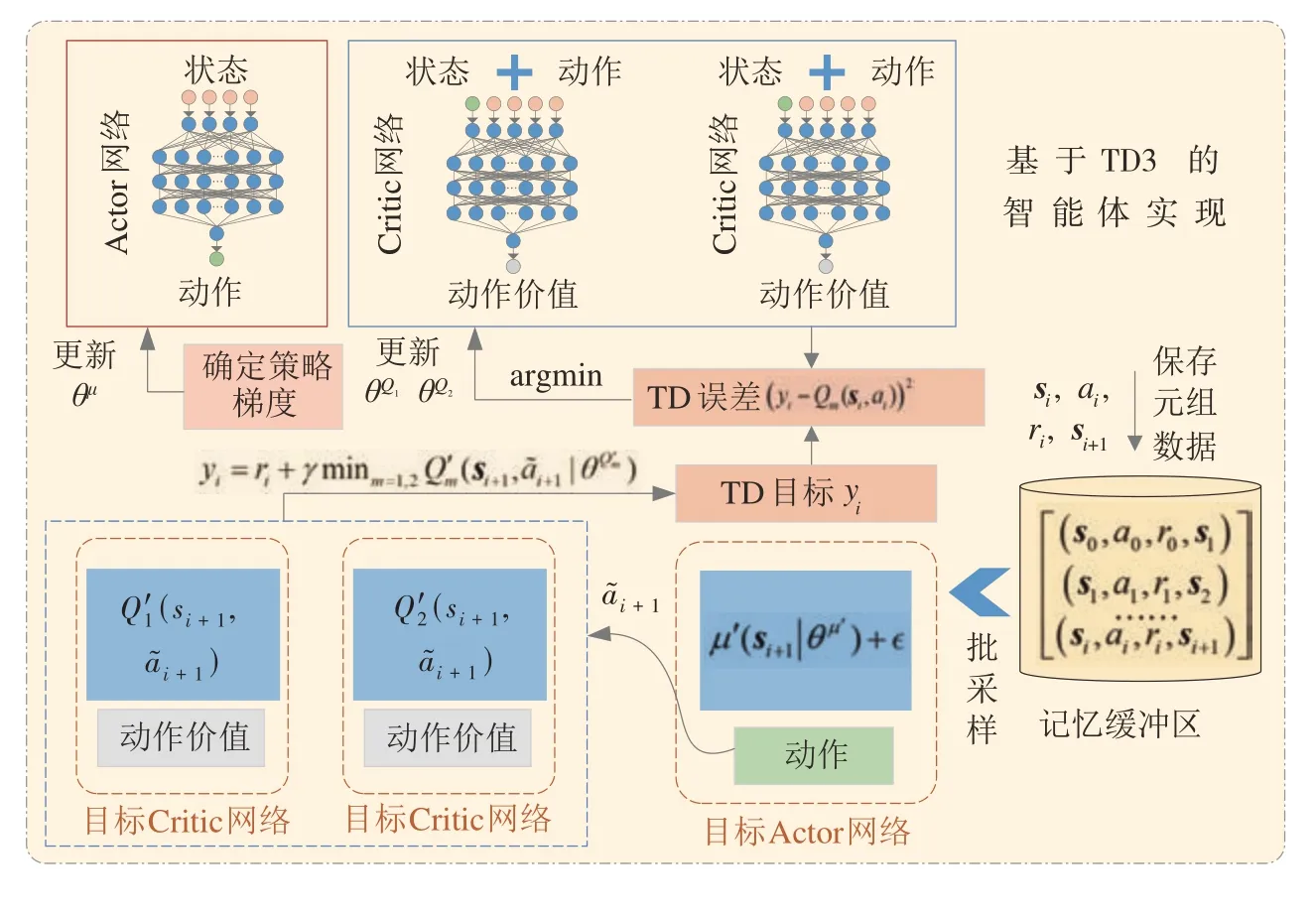
图4 基于TD3的生态驾驶智能体实现
在每一控制步中,TD3 智能体根据式(10)观测的状态向量利用Actor 网络计算动作ai。为了将智能体输出的车辆加速度限制为[-3,3] m/s2,Actor 网络的输出层添加了一层双曲正切函数层(tanh 层)。tanh 层使得Actor 网络的输出限制到[-1,1]之间,然后根据设定的实际车辆加速度范围对其乘3 进行缩放。因此在训练过程中TD3智能体规划的车辆加速度可以表示为
式中:N为训练过程中的高斯探索噪声。
每一控制步的观测状态si、Actor 网络计算的动作ai、采取动作ai后的下一步状态si+1以及奖励函数计算的相应奖励值ri被组成一个数据元组(si,ai,ri,si+1)存入记忆缓冲区R中。在训练过程中定期从R中随机批采样M组元组数据用于更新Actor与Critic网络。
批采样的每个数据元组的动作价值与时序-差分(temporal difference,TD)目标为
Critic 网络参数更新可以通过最小化TD 误差的平方实现[22]:
Actor 网络的参数可以根据确定性策略梯度法更新[23]。
本文中所使用的TD3 智能体的超参数以及Actor 与Critic 网络的结构如表1 所示。这些超参数和网络结构是通过反复试错调整而得到的。TD3智能体由Python 语言编程为库函数,在算法训练时通过s-function模块在Simulink模型中调用。
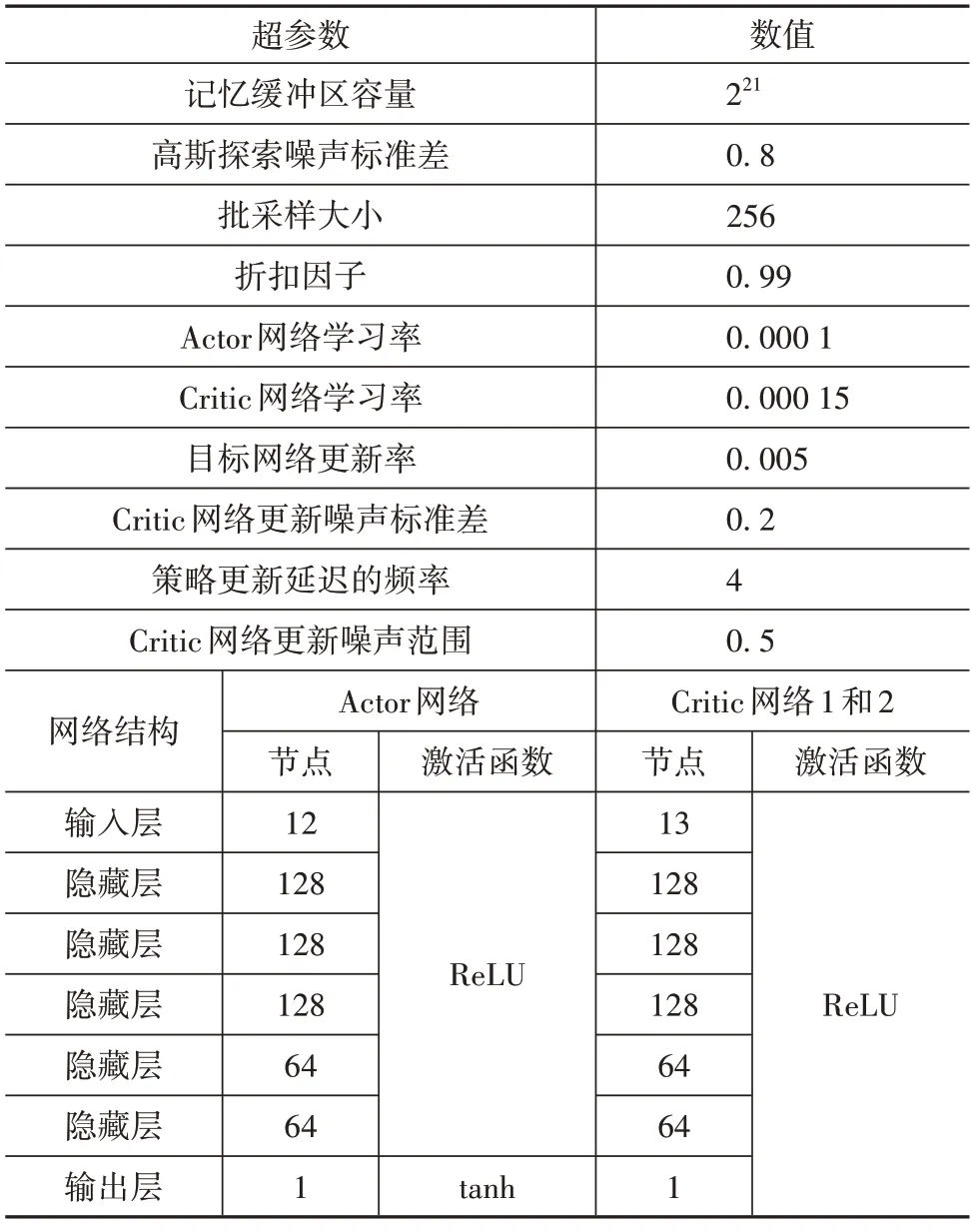
表1 TD3智能体超参数与网络结构
2.6 车速跟踪控制器设计
为了控制CAV 跟踪生态驾驶策略规划的参考车速,本文设计了一个简单而有效的基于比例-积分-微分(proportion integration differentiation,PID)的车速跟踪控制器。底层车速跟踪控制框架如图5 所示,通过参考车速与反馈的实际车速之差计算驱动电机输出转矩。
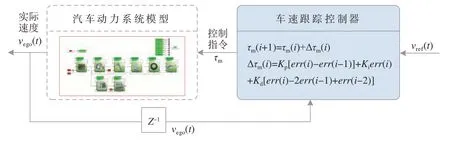
图5 底层车速跟踪控制框架
式中:Kp、Ki与Kd分别为PID 控制器的比例、积分和微分增益;err为参考车速vref与车辆实际车速vego之差。
3 算法验证
3.1 硬件在环实验平台设计
为了分析所提出的基于DRL 的生态驾驶策略性能,本文在HIL 平台上对算法进行了实验验证。如图6 所示,该HIL 平台主要包括车辆仿真模块、控制器模块与虚拟场景模块组成。各模块之间通过CAN总线进行数据通信。

图6 HIL实验平台原理图
车辆仿真模块由Speedgoat 公司开发的实时仿真器[24]实现。仿真器上运行的高精度车辆动力系统模型由美国阿贡国家实验室研发的车辆动力系统建模软件Autonomie[25]建立。该模型通过仿真器上位机编译后下载入实时仿真器,在HIL实验时启动以模拟真实的车辆。仿真车辆的参数详见表2。此外,仿真器上位机还用于实时监测CAN总线上的数据流。
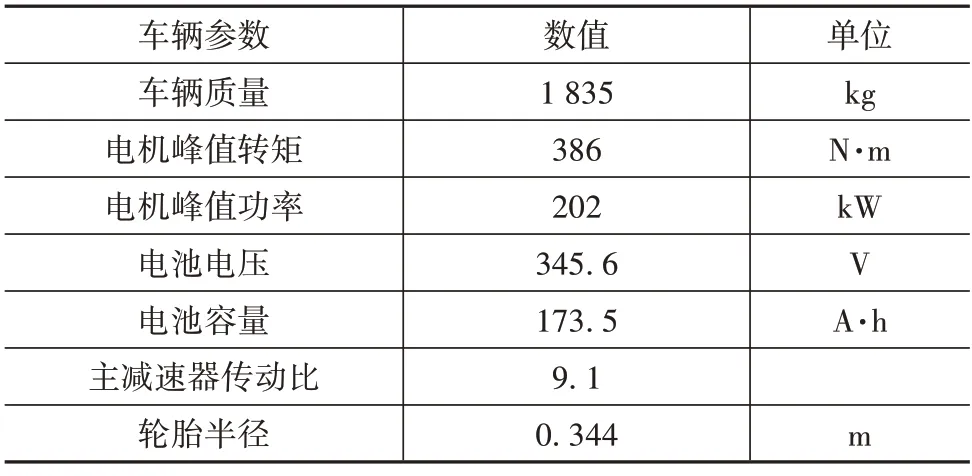
表2 车辆动力系统参数
HIL 平台的控制器模块采用一款基于英飞凌车规级芯片TC275T 开发的VCU。生态驾驶策略在Simulink 中建模并编译为.hex 文件后,通过刷写工具刷写到VCU中,在HIL实验时实时控制车辆运动。
虚拟场景模块负责模拟真实道路的复杂交通环境并在CAN 总线中实时广播虚拟车辆感知的交通状态信息。本文中虚拟交通场景仿真使用开源城市交通仿真软件(simulation of urban mobility,SUMO)[26]来实现。SUMO 中搭载的城市交通仿真模型根据德国TAVF(test track for automated and connected driving)计划[27]发布的汉堡市交通数据建立。如图7所示,被控车辆在虚拟场景中的预期行驶路线全长约7 060 m,沿途限速为50 km/h,共经过27 个交通灯路口。
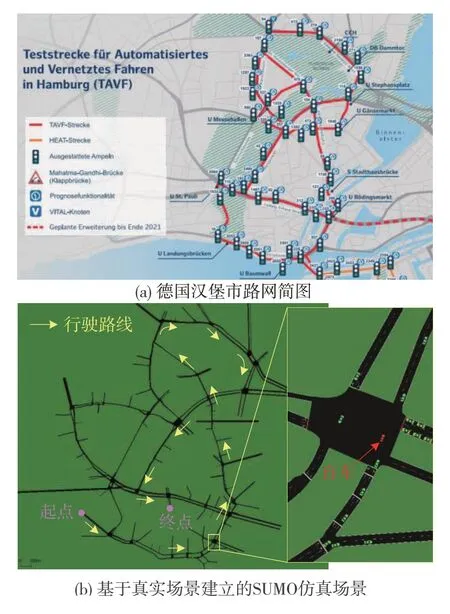
图7 虚拟交通场景
3.2 算法迭代训练结果
为了将所提基于DRL 的生态驾驶策略用于实时控制,首先需要将TD3 智能体训练至累积奖励值收敛到稳定状态。本文中最大训练轮次被设置为300轮,每轮训练的车辆行驶里程被设置为3 500 m。训练过程在一台具有AMD 4800U 处理器的笔记本电脑上完成,总训练时间为19.04 h。训练过程的奖励轨迹如图8所示。
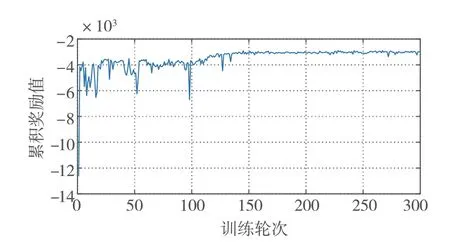
图8 所提算法总奖励曲线
由图8 可见,在训练过程的开始阶段,由于网络的训练还不足,TD3 智能体倾向于充分探索整个环境,每个回合的累积奖励虽然呈现上升趋势但波动较大。随着训练轮次的增加,从第100 轮到150 轮,TD3 智能体逐渐意识到最优策略的存在,总奖励开始稳步上升。当TD3 智能体训练到150 轮之后,已经达到收敛状态,累积奖励轨迹相对稳定。但由于Actor 网络计算的动作添加了高斯探索噪声,累积奖励值仍在一个小范围内波动。总的来说,随着训练轮次的增加,累积奖励值呈现上升趋势,表明本文设计的状态空间、动作空间和复合奖励函数可以使得DRL智能体学习最优策略。
离线训练完成后,提取训练过程收敛阶段内单轮训练累积奖励值最高的Actor 网络的节点权重和偏差值。在Simulink 中构建基于训练后Actor 网络与安全速度建议模块的生态驾驶策略模型,编译后下载入HIL实验平台的VCU中进行算法性能验证。
3.3 算法性能对比分析
为了全面分析本文所提基于DRL 生态驾驶策略的优化性能,本文根据文献[4]与文献[28]中提到的智能驾驶员模型(intelligent driver model,IDM)设计了基于IDM的对比生态驾驶策略作为基准。由于经典IDM 模型仅适用于跟车任务[29],为了遵守交通灯规则,设计了基于IDM 的对比策略框架,如图9 所示。该框架与所提基于DRL 的生态驾驶策略一致,只是将DRL智能体替换为IDM模型。
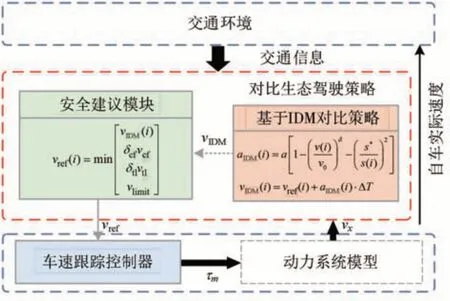
图9 基于IDM的生态驾驶策略框架
对比策略中IDM模型计算的参考车速为

表3 实验结果对比

图10 两种策略车辆行驶轨迹时空图

图11 虚拟交通场景中自车与前车的距离信息以及前车的车速信息
从图10 中可以看出,两种策略都能满足交通灯规则的约束,没有发生闯红灯行为。此外,由于HIL平台中基于SUMO 的虚拟交通场景可以动态模拟真实车辆的变道和超车行为,因此被控车辆前方的车辆是可以随时发生变化的。即使在这样具有挑战性的场景中,如图11 所示,被控车辆与前车之间的距离始终大于零,表明整个行程都没有发生碰撞事件。可以说明本文所设计的考虑速度建议模块的生态驾驶策略框架能够有效地控制车辆在复杂城市交通环境中安全行驶。此外,表3 中所提策略控制的自车在实验过程中与前车的最小距离比对比策略高10.41%,说明所提策略更加安全可靠。
关于乘坐舒适性,如图12 所示,对比IDM 策略在加速度为-2、2 和0 m/s2附近的频数高于所提策略。而所提策略加速度更集中于[-1,1] m/s2的加速度区间。这是因为式(8)所提策略的奖励函数考虑了加速度奖励项,因此所提策略更倾向于采取较小的加速度,以较为温和的方式控制车辆加速/减速至目标车速。相比之下,对比IDM策略则更加激进,先通过较大的加速度调整车速,再匀速行驶。两种策略的加速度量化的对比如表3 所示,所提策略的加速度绝对值平均数小于对比IDM 策略。因此,所提出的策略比对比IDM策略更舒适。
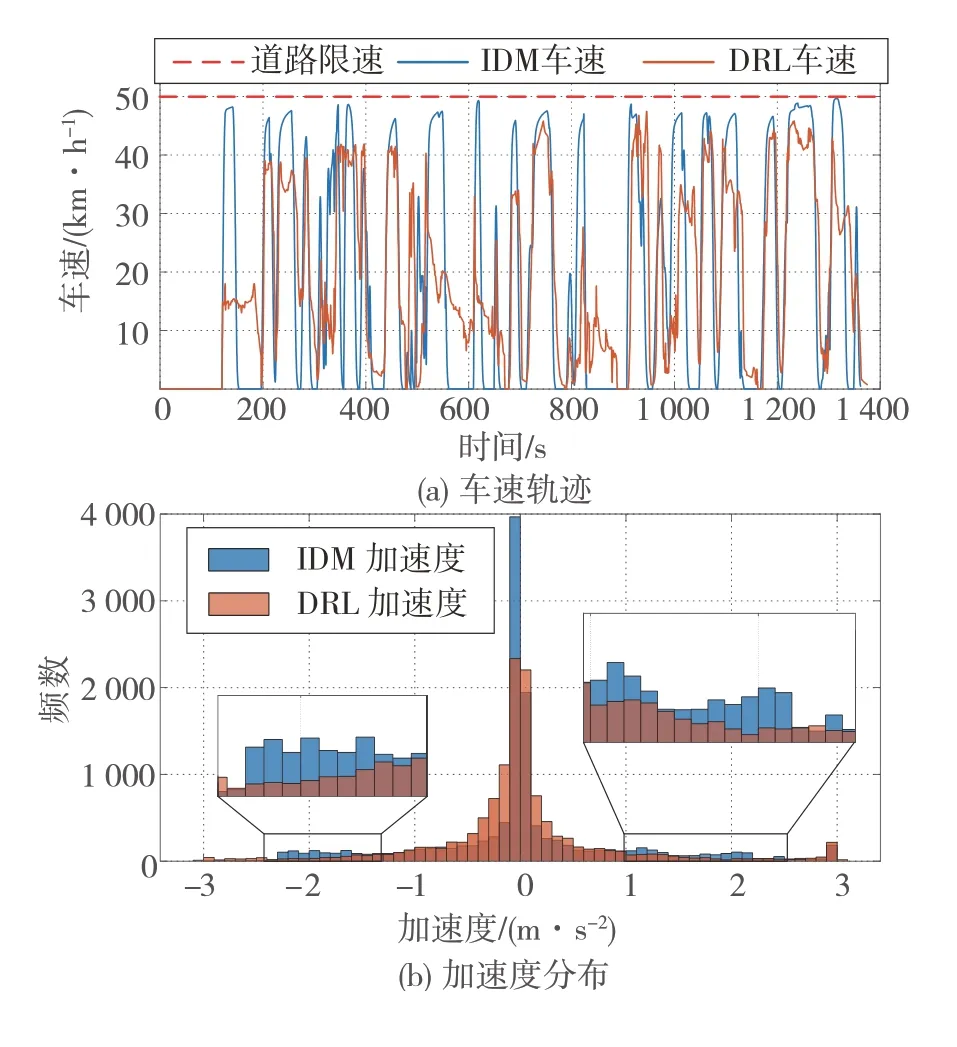
图12 两种策略的车速轨迹与加速度分布
在经济性方面,由于式(8)所提策略的奖励函数包括电池能耗项,基于IDM 的生态驾驶策略通过训练学到了优化车速以提高电能使用效率。从图13电机功率损失分布图以及表3 的电机损失电能项可以发现,所提策略的电机功率损失小于对比IDM 策略的电机功率损失。因此,如表3 中的电池电耗项所示,与对比IDM策略相比,所提策略的用电量降低了10.94 %,证明了所提策略具有良好的能耗经济性。

图13 两种策略的电机机械功率与电机功率损失分布
最后,在行驶效率方面,虽然表3 所示所提策略的总行驶时间与基于IDM的策略总行驶时间大致相同,但相较于对比IDM 策略,所提策略减少了83.38%的红灯停车等待时间。这一点也可以从图10 的示例段(a)、(b)、(c)和(d)中看出,所提策略相对于对比IDM 策略在交通灯路口停车次数更少,整个行程更加通畅。因此,所提策略的综合驾驶体验比对比IDM策略更好。
为了充分展现本文所提DRL 策略的有效性和实用性,选择了图10 中仿真时间范围为250-350 s的示例段(a)对所提策略展开了具体案例分析。此外,由于V2X 通信在实际应用中必然存在时延问题,进行了不同传输时延场景下的HIL 实验验证。结果表明,当时延小于500 ms 时,时延对控制算法性能的影响不大;而当时延大于500 ms 后,需要补偿传输时滞以克服对算法安全性带来的负面影响。
4 结论
本文提出了一种改善复杂城市场景下纯电动CAV乘坐体验的多目标生态驾驶策略。通过设计包含安全速度建议模块的生态驾驶策略框架,保证了被控车辆的安全性;并通过设计融合安全约束与塑形函数的多目标复合奖励函数实现了经济性、舒适性和出行效率的协同优化。在基于虚拟交通场景的HIL 平台下的实验结果表明,所提策略可以在确保驾驶安全的前提下,实时协同优化车辆的能耗经济性、舒适性和通行效率。与基于IDM对比策略相比,所提策略的电耗降低了10.9 %,证明了所提方法的有效性。为了更好地优化CAV 的驾驶行为,未来的研究可以进一步完善该策略,并将其应用于更广泛的交通场景中。此外,也可以探索更多的DRL 模型,以更好地提高汽车的行驶效率和安全性。

