超磁致伸缩式喷油器的结构参数优化及其响应特性研究
喻曹丰,段永勇,王玉,肖志豪,吴干,魏梓贤
(安徽理工大学机械工程学院,安徽淮南 232001)
0 前言
高压共轨喷油系统具有高压喷油、喷油速率柔性控制等优点,已成为柴油机燃油喷射系统的主流[1]。喷油器作为高压共轨喷油系统的终端,其响应特性直接影响燃油喷油规律,进而影响柴油机的性能[2]。目前主要的喷油器驱动形式为电磁式与压电式两种,但电磁式响应时间长,不能对输出位移进行调节,而压电式的输出位移小且居里温度低,因而限制了喷油器的发展。为进一步提高喷油器的响应性能,可采用超磁致伸缩材料(Giant Magnetostrictive Material,GMM)作为喷油器驱动元件。GMM具有响应速度快、精度高、输出位移大、可靠性高等优点[3],因此以GMM为换能元件的超磁致伸缩驱动器(Giant Magnetostrictive Actuator,GMA)可弥补电磁式和压电式驱动器的缺陷。
超磁致伸缩式喷油器(Giant Magnetostrictive Injector,GMI)工作过程涉及电-磁-机-液多场耦合[4-6],目前GMI结构设计与建模的主要研究成果有:薛光明等[7-8]设计出一种零偏置的GMI,提出了适当的驱动波形,并在AMESim中建立仿真模型,通过仿真与试验验证了其结构的喷油特性;HE等[9]设计一种GMM直驱针阀式喷油器,并将其简化为单自由度振动模型,推导出其运动学模型,研究了针阀初始位置与初始速度对针阀撞击的影响;徐彬[10]将GMM与柔性机构结合,通过柔性机构实现对GMM输出的换向与放大,实现了对针阀的控制,通过研究其动力学模型,得到了结构设计参数与针阀动态响应性能之间的关系。
综上,已有研究在GMI建模中缺少将GMM磁滞非线性特性耦合于喷油器模型[11],因此不能充分揭示超磁致伸缩式喷油器的性能特性。作者提出一种液压传动式GMI,基于Jiles-Atherton模型描述GMM的磁滞非线性特性,建立GMA输出力模型,同时建立喷油器液力系统数学模型,并在MATLAB/Simulink模块中建立耦合仿真模型,验证结构的可行性;同时研究了GMM棒预应力对球阀输出的影响;最后采用遗传算法,对GMA的预应力、进出油孔直径、控制腔容积等关键参数进行优化。
1 GMI结构设计与工作原理
GMI的结构示意如图1(a)所示,分为GMA与机液部分,其中GMA实现电能-机械能的转变,而机液部分实现喷油功能。
GMA核心元件GMM棒由材料Tb0.3Dy0.7Fe2制成,GMM棒工作原理是将供磁机构提供的磁能转换为自身应变,对外输出力与位移。双线圈式供磁机构具有良好的平均磁场强度与磁场均匀度,因此GMA采取双线圈式供磁,其中内线圈产生驱动磁场,外线圈产生偏置磁场。同时此结构通过预紧螺钉与碟簧的组合为GMM棒提供预应力,以改善GMM棒的驱动性能。
喷油器机液部分以球阀式喷油器为基础,通过GMM棒驱动球阀,打开球阀口。同时此结构GMM棒在轴向的输出是伸长的,需借助换向机构将GMM棒输出位移进行换向。而液压传动具有结构紧凑、承载能力大的特点,因此采用液压传动机构对GMM棒输出位移进行换向,采用的位移换向机构如图1(b)所示,其工作原理为当上活塞下行时,位移换向上腔压力增大,因位移换向上、下腔连通,则位移换向下腔的压力也增大,则下活塞受液压力的作用上行。
结合图1,GMI工作过程为:激励线圈与偏置线圈通入相反的电流,使磁场叠加为0,GMM棒处于零位状态。喷油器工作时,激励电流增大,在叠加磁场下,GMM棒发生应变,带动上活塞对位移换向上、下腔增压,球阀组件在位移换向下腔的液压力作用下,向上运动打开球阀口,控制室的压力降低,针阀组件受上液压力大于下液压力,从而打开喷孔实现喷油;当激励电流恢复初值后,GMM棒恢复原长,位移换向上、下腔压力降低,球阀杆在球阀弹簧的作用下关闭控制腔出油孔,控制腔压力恢复,针阀在控制腔液压力的作用下,向下运动,喷孔关闭,喷油结束。设计的GMA最大输出位移为35 μm,球阀最大位移为50 μm,针阀的最大位移为0.35 mm。图2为GMI工作流程。

图2 GMI工作流程
2 GMI建模
基于GMI的结构与工作原理,其数学模型包括多个子系统,但主要可分为GMA模型和液力系统模型两个部分。GMA模型包括电流、磁场强度、磁化强度、磁致伸缩系数与输出力模型;而液力系统包括位移换向上腔、位移换向下腔、控制腔、输出杆组件、球阀与针阀组件模型。
2.1 GMA模型
该GMA采用驱动线圈与偏置线圈共同驱动,即通过电流的磁效应对GMM棒提供磁场。电流与叠加磁场之间的关系:
H(t)=Hq+Hp=fqNqIq(t)+fpNpIp
(1)
式中:H(t)为GMA叠加磁场;Hq为驱动线圈产生的磁场;Hp为偏置线圈产生的磁场;fq为驱动线圈磁场系数;fp为偏置线圈磁场系数;Nq为驱动线圈匝数;Np为偏置线圈匝数;Iq(t)为驱动线圈电流;Ip为偏置线圈电流。
由于GMM材料具有磁滞非线性特性,因此需要建立叠加磁场与材料磁化强度之间的关系。基于修正后的Jiles-Atherton模型建立GMM棒磁滞模型,在模型中同时考虑预压应力[12],则外加磁场H与磁化强度M的关系如下:
(2)

经推导得出适合建模的形式:
(3)
c、α、a、k、Ms需通过参数辨识获得,在此直接引用,其值[13]如表1所示。

表1 参数辨识结果
根据二次畴转模型,对于各向同性的材料,可得到磁致伸缩应变λ与GMM棒内磁化强度M关系为
(4)
式中:λs为饱和磁致伸缩系数,λs=1 500×10-6。
根据材料力学知识,可知GMM输出力FGMM为
FGMM=EHArλ
(5)
式中:EH为GMM棒的弹性模量;Ar为GMM棒的横截面积。
将GMA简化为单自由度的质量-阻尼-弹簧系统[14],如图3所示。

图3 GMA输出简化图
GMM棒与输出杆的力平衡方程为
(6)
式中:mtot为GMM棒与输出杆等效质量,mtot=mGMM/3+msh;cM为GMM棒等效阻尼系数,cM=cDAr/L,cD=3×106N·s/m2,L为GMM棒长度;kM为GMM棒等效刚度系数,kM=ArEH/L;Fspr为碟簧预压力;Fu为位移换向上腔对输出组件的力,Fu=pouAu。
2.2 液力系统模型
基于质量守恒方程与力守恒方程建立一维湍流可压缩的液力系统模型,作以下假设[15]:
(1)腔室假定为集中容积,且不考虑压力传播的时间;
(2)忽略密封件之间的泄漏;
(3)出油孔的横截面积正比于x/Xmax,其中x为移动件位移,Xmax为移动件最大位移;
(4)各部件视为刚体,不考虑其变形;
(5)动能在碰撞中完全耗散。
常温常压下,柴油的密度一般为ρ=820~880 kg/m3,在此取中间值850 kg/m3。柴油具有可压缩性,可通过有效体积模量β描述:
(7)
式中:p为柴油的压力。
位移换向上、下腔实现对GMA输出位移的换向与放大,忽略管道效应,即位移换向上、下腔压力相等,其简化模型如图4所示,则其流体连续性方程为
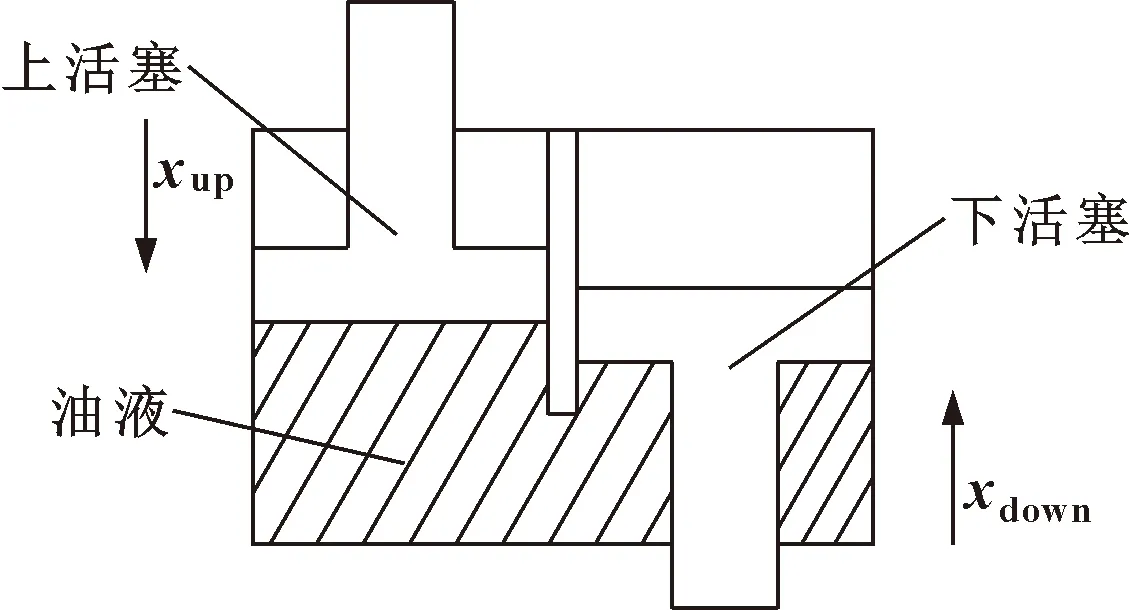
图4 位移换向上、下腔简化模型
(8)
式中:pou为位移换向上、下腔等效压力;Vou为位移换向上、下腔总容积,随两个活塞位移而改变;xup为上活塞位移量;xdown为下活塞位移量。
球阀在位移换向下腔的作用下,克服球阀弹簧预紧力,从而打开球阀口。喷油结束后,球阀在弹簧力的作用下,克服控制腔液压力关闭球阀口。球阀受力如图5所示。

图5 球阀受力简图
由牛顿第二定律可知,球阀力平衡方程为
(9)
式中:mq为球阀组件的质量;kqs为球阀弹簧刚度;cqs为球阀组件的阻尼系数;Fd为位移换向下腔对球阀组件的力;Fqs为球阀弹簧的预紧力;Fy为控制腔对球阀组件的力。
控制腔的压力与进油量、出油量以及针阀组件的运动位移和速度有关,据此可对控制腔的压力pco进行建模:
(10)
式中:
(11)
(12)
式中:Vco为控制腔容积,与针阀组件的位移有关;xzh为针阀组件的位移量;xq为球阀组件的位移量;Xq为球阀组件的最大位移量,为0.35 mm;qin为控制腔入口流量;qout为控制腔出口流量;Azh为柱塞上表面积;Cdin、Cdout分别为进油孔与出油孔流量系数,对于细长孔其值可取0.82;Ain为进油孔面积;Aout为出油孔面积。
因为研究单次喷射,假设蓄压腔压力与轨压相同,当控制腔压力降低时,针阀组件在其底部液压力的作用下,克服弹簧预紧力向上运动,进而打开喷孔;当控制腔压力恢复后,针阀又在弹簧与控制腔液压力的作用下,关闭喷孔,针阀受力如图6所示。
由牛顿第二定律可知,针阀组件力平衡方程为
(13)
式中:mzs为针阀组件质量;czs为针阀弹簧阻尼系数;kzs为针阀弹簧刚度系数;Fdh为Fzm与Fzd之和,Fzm为针阀组件在蓄压腔受力,Fzd为针阀组件的底部受力。
针阀孔喷油率计算公式为
(14)
式中:n为喷孔数量;Cdinj为喷孔的流量系数;Xzh为球阀组件的最大位移量;Ainj为喷孔的截面积;pc为汽缸内压力。
对喷油率进行积分,可以获得喷油量Q计算公式为
(15)
2.3 GMI模型搭建
通过MATLAB/Simulink模块建立J-A模型具有很大的优势,因此根据上述数学模型,采用MATLAB/Simulink模块搭建GMI模型。模型的输入为驱动线圈电流、偏置线圈电流与轨压。求解器为定步长的四阶龙格-库塔,仿真时间为8 ms,步长为1 μs。GMI系统仿真模型如图7所示,GMI主要参数如表2所示。

表2 GMI主要参数

图7 GMI的Simulink仿真模型
3 GMI响应性能研究与优化
3.1 GMA性能研究
GMA驱动性能对喷油器性能有很大的影响,由式(5)可知,GMM棒输出力与磁致伸缩系数成正比,因此可通过研究磁致伸缩系数,进而对GMA的输出特性进行分析。不同偏置磁场下的GMM棒磁致伸缩系数曲线如图8所示。

图8 不同磁场下的磁致伸缩系数曲线
由图8可知:由于GMM材料的磁滞特性,当驱动磁场恢复初值时,GMM棒存在残余的磁致伸缩系数,并且值小于4×10-5,由式(5)(6)计算可知,GMA输出不足以打开球阀口,因此GMM材料的磁滞特性不会影响喷油器的工作。同时在偏置磁场下,GMM棒磁致伸缩曲线具有更大的线性区间,这有利于实现对输出的控制。
GMM棒预压应力可以提高GMM棒的输出性能,但当预压应力过大时,反而会导致性能降低。工况选定为轨压100 MPa,偏置电流1.5 A,驱动电流-0.8~0.2 A。分别取0、1、2、3、4、5、6 MPa下GMM棒预应力研究球阀的响应情况,驱动电流波形如图9所示,上升时间与下降时间为0.1 ms,不同GMM棒预应力下的球阀响应如图10所示。

图9 驱动电流

图10 不同预应力下球阀开启位移
由图10可知:随着GMM棒预应力从0 MPa增加到3 MPa,球阀响应性能得到提升;而当GMM棒预应力从3 MPa增加到6 MPa后,球阀的响应性能降低。同时当预应力处于3 MPa时,球阀开启延迟为34 μs,上升时间为158 μs,因此GMA式喷油器的响应迅速。
3.2 基于遗传算法的喷油器优化
为获得优良的喷射响应性能,对GMI关键参数进行优化是必不可少的。利用遗传算法可实现全局收敛从而得到最优解,并得到GMI喷射性能的最佳参数组合。选取针阀位移各阶段时间作为喷油器喷射性能的评价指标,各阶段时间可定义为针阀开启延迟t1、针阀上升时间t2、针阀关闭延迟t3和针阀下降时间t4,如图11所示。

图11 喷油器响应性示意
采用综合评分法评价GMI的响应性能,因喷油器需满足缓开急关的喷油特性与多次喷射能力的需求,选取t1、t2、t3、t4的权重为
t=0.2t1+0.25t2+0.25t3+0.3t4
(16)
结合前文所述与文献[16],对GMM棒预应力,控制腔容积,进、出油孔直径与针阀弹簧预紧力进行优化,优化变量原值与取值范围见表3。在MATLAB中编写遗传算法程序进行优化,工况不变,以t值最小为目标,设定种群大小为100,复制概率为80%,变异概率为1.5%,迭代次数为50次。

表3 优化参数的原值与范围
3.3 优化结果分析
每代最优适应度和迭代次数关系如图12所示。可知:在第12代后,适应度达到最小值,可以认为满足算法终止条件。最终优化的参数值:GMM棒预应力为2.65 MPa;进油孔直径为0.300 mm;出油孔直径为0.749 mm;控制腔容积为8.153 mm3;针阀预紧力为67.8 N。
表4为优化前后的针阀响应特性计算结果,结果显示针阀的开启延迟与关闭延迟得到显著降低,针阀响应性能有所提高。

表4 针阀响应特性的优化结果
图13为优化前后的针阀运动升程对比,可以看出:参数优化后GMI的针阀运动得到了很大改善,响应速度得到了提高,可以获得理想的喷油规律,同时有利于精准控制喷油正时,可使柴油机获得理想的燃烧状态,降低有害排放。

图13 优化前后针阀响应特性对比
4 结论
(1)提出一种超磁致伸缩式喷油器的设计方案,其主要工作原理是GMM棒通过位移换向上、下腔实现对球阀的控制。同时将超磁致伸缩驱动器的输出力模型与喷油器的机-液部分耦合,建立了完整的超磁致伸缩式喷油器电-磁-机-液多场耦合模型。
(2)在MATLAB/Simulink中搭建超磁致伸缩式喷油器仿真模型,通过仿真验证了GMM棒的磁滞特性不会影响喷油器工作,研究GMM棒预应力对球阀输出特性的影响,得到最佳预应力在3 MPa附近。
(3)采用遗传算法优化了喷油器的5个关键参数,相较于原参数方案,优化后针阀开启延迟缩短了27.3%,开启时间减小了11.0%,关闭延迟缩短了19.5%,关闭时间减小了9.9%,针阀响应特性获得了较大程度的提升,可得到理想的喷油规律,降低有害气体的排放。

