数控机床直线进给系统相位特性的建模与分析
王泓元,胡亚辉,张现,张大卫
(1.天津理工大学海运学院,天津 300384;2.天津大学机械工程学院,天津 300350)
0 前言
直线进给系统是数控机床的核心部件之一,是数控机床的主要传动方式[1]。多轴联动机床加工过程中,需要多轴进给系统共同完成三维空间的加工,而各个轴的进给系统的动态特性呈现复杂变化的特点[2],因此多轴耦合过程中误差增加。直线进给系统运行过程中,由于工况复杂,其参数的变化会使输出信号的响应规律发生改变。因此,借助动力学模型仿真方法对进给系统参数变化进行建模仿真,求得进给系统相位特性变化规律,对进给系统的动态特性研究与机床的轴间耦合研究有着重要的意义。
近年来,对于进给系统的动态特性国内外学者开展了大量的研究。王磊等人[3]建立集中参数的动力学模型,验证了轴间耦合作用对多轴联动机床的动态特性有较大的影响,通过加速度的频率响应曲线得出三轴机床不同刀尖点具有不同动态特性。HUNG等[4]基于Hertz接触理论对滚动结合面的刚度进行分析,确定了滚动部件的动刚度与振动模态的关系,可用于评估不同滚动部件对机床系统整体动态性能的影响。VICENTE等[5]建立了进给系统的高频动态模型,将滚珠丝杠建模为一个连续的子系统,从而为控制器的参数设计提供参考,降低轨迹的跟踪精度。然而对进给系统的动态特性研究[6-10],目前多以进给系统首阶与次阶固有频率作为衡量指标,分析固有频率变化规律,弱化工况变化对固有频率的影响,使进给系统的动态特性更稳定。若想对各个轴向进给系统的动态误差进行量化,从结构与控制等方面对多轴耦合误差进行补偿,需对进给系统动态特性有着更详细的衡量指标。
因此,本文作者针对进给系统的输出信号与输入信号之间的相位特性变化规律进行研究。建立进给系统的集中质量动力学模型,并结合进给系统运行过程中的不同工况,对动力学模型参数变化规律进行分析。通过动力学模型的仿真,分析参数变化对进给系统相位特性的影响。
1 直线进给系统动力学模型
将进给系统的伺服电机、丝杠、螺母与工作台理想化为集中质量块,建立进给系统的集中质量模型。简化后的质量块之间存在刚度特性与阻尼特性,因此将部件之间的结合面简化为非线性的弹簧阻尼单元,其中丝杠自身的刚度与轴承刚度进行串联。建模方法的精度与可靠性已在文献[11]中得到验证。
根据达朗贝尔原理可得直线进给系统的动力学模型为
(1)
其中:M10×10、C10×10、K10×10分别为系统的质量矩阵、阻尼矩阵与刚度矩阵;F10×1为外部对进给系统的激励;x为部件对应的位移。
2 直线进给系统参数分析
由于加工过程中工况复杂,进给系统工况不同,部分动力学模型参数会发生改变,对会发生变化的系统参数进行分析。
2.1 导轨滑块副静刚度分析
导轨滑块副由滑块、滚柱与导轨共同组成,其简化模型如图2所示。导轨直线度误差是进给系统误差重要来源之一。进给系统运行过程中,导轨误差不同会使导轨滑块副的静刚度改变。
其中ei为导轨的直线度误差,当导轨误差变化,会使滑块内滚柱、滑块裙边、工作台甚至导轨表面产生弹性形变。但由于工作台与导轨表面刚度远大于其他部分刚度,因此可将二者理想化为刚体。导轨直线度误差发生变化时,滚柱会因直线度误差的变化发生弹性变形,而弹性力的作用在滑块裙部因变形会释放滚动体的压缩变形量,二者达到平衡状态。
基于赫兹接触理论的经验公式[12],滚柱内部接触力与变形量之间关系为
Q=Cδ10/9
(2)
(3)
其中:Q是滚柱轴向的法向载荷;δ为滚珠接触变形;ν1、ν2分别为滚柱与滚道面泊松比;E1、E2分别为滚柱与滚道面的弹性模量;l0为滚柱长度。
将法向载荷Q分解到水平、垂直方向,且法向载荷Q与水平轴夹角均为45°。因此滚动体的等效刚度为
(4)
其中:kx1、ky1分别为滚动体水平与垂直方向的等效刚度。
其中:Q为滚柱作用于滑块裙边的弹性力。滑块裙边可简化为悬臂梁结构,等效刚度为
(5)
其中:Fs为滚柱对滑块裙边的弹性力;Eh为滑块裙部的弹性模量;I为裙部的截面惯性矩;lh为滑块裙部悬臂梁长度的一半。因此导轨滑块副等效刚度简化模型如图4所示。
将公式(4)、(5)刚度计算公式代入公式(6)、(7)中,计算出导轨滑块副等效模型水平与垂直静刚度
(6)
k1y=k2y=ky1
(7)
其中:k1x、k2x为导轨滑块副水平刚度,由滚柱等效刚度与滑块裙边等效刚度串联求得;k1y、k2y为导轨滑块副垂直刚度。
2.2 工作台摩擦力分析
摩擦力计算与正压力相关,首先需对工作台内部弹性力进行求解。工作台与4个滑块由螺栓进行固定连接,某一滑块受力情况发生变化时,所有滑块均发生改变,最终工作台达到受力平衡,如图5所示。
利用力学平衡可对4个导轨滑块的4个方向等效结合面的变形量进行求解:
(8)
式中:δxi,1、δxi,2、δyi,1、δyi,2分别为X正方向、X负方向、Y正方向、Y负方向的滚柱变形量;exi,1、exi,2、eyi,1、eyi,2分别为对应方向的导轨直线度误差;ξi,1、ξi,2为滑块裙边变形量;g为等效模型的预紧压缩量;xi、yi分别为滑块在X、Y方向的位移量;i=1,2,3,4对应工作台的4个滑块。
将式(2)—(7)代入式(8)可求得对应导轨滑块副的刚度系数弹性力:
(9)
其中:Fx与Fy分别为导轨滑块副水平与垂直方向等效弹性力;kx、ky为代入公式(6)、(7)求得的刚度系数。将弹性力作为结合面的正压力FH,与摩擦因数μ相乘可得摩擦力,将4个滑块摩擦力求和,可求得工作台受到的总摩擦力:
(10)
其中:FxHi、FyHi分别为4个滑块与导轨的等效正压力;Ff为工作台受到的总摩擦力。
2.3 丝杠轴向静刚度变化分析
丝杠的轴向拉压刚度反映了进给系统受到轴向作用力的抗变形性能。由于丝杠采用一端固定一端自由的支撑方式,因此由螺母传递的轴向力作用点与固定端之间的丝杠部分会发生改变。工作台位置发生变化时,丝杠的轴向刚度会随之改变,其计算公式为
(11)
式中:Ksa为丝杠轴向拉压刚度;E为丝杠材料的弹性模量;A为丝杠螺纹部分最小截面积;d为丝杠的螺纹底径;xs为载荷作用点到固定端轴承的轴向距离,会随着工作台位置变化而改变。
3 进给系统动力学模型参数确定
结合具体工况,确定进给系统动力学模型参数。
3.1 动力学模型参数规律分析
动力学模型包括进给系统的质量矩阵、刚度矩阵与阻尼矩阵,通过计算,不随工况改变而变化的进给系统动力学模型参数如表1所示。
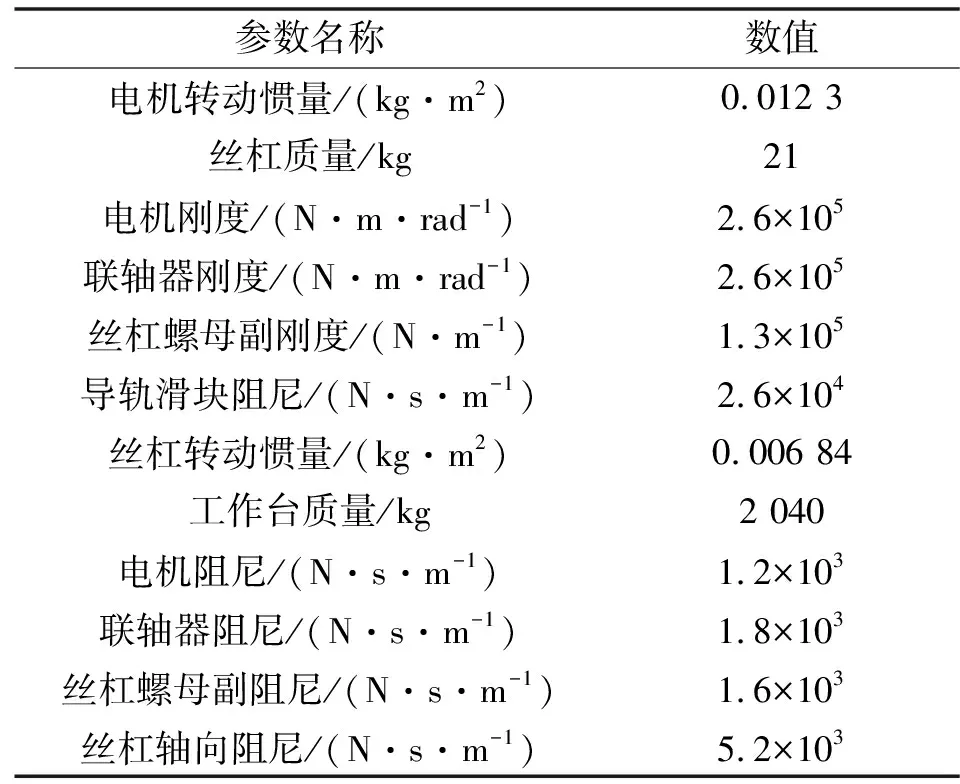
表1 动力学模型参数
机床制造过程中为补偿导轨梁在重力作用下的弯曲变形,会对导轨进行反变形补偿,因此导轨直线度误差呈拱形[13]。实际测量结果验证了这一现象[14],如图6所示。
因此本文作者将直线度误差简化为水平与垂直的拱形误差,探究工作台位置改变过程中,导轨直线度误差变化对内部参数的影响。
(12)
(13)
其中:ex(z)、ey(z)分别为X、Y方向直线度误差;Z为工作台位置;L为工作台总行程;e0为导轨误差最大值,在导轨中点取得。
工作台有效行程L为900 mm,以150 mm为步长,表2为导轨滑块副参数,将数据代入公式(2)—(9)中可求得导轨误差对导轨滑块副刚度系数与弹性力的变化规律。

表2 导轨滑块副参数
图7(a)与图7(b)分别为出现拱形误差时,4个滑块刚度系数变化规律。图7(c)为导轨滑块副平均弹性力,由于X方向为滚动体与裙边共同作用,与Y方向相比弹性力较大。图7(d)为位置改变丝杠轴向刚度的变化规律。综合图7可得:工作台位置改变过程中,进给系统的部分动力学模型参数会发生改变。
3.2 工作台摩擦力
工作台位置变化弹性力发生变化,工作台摩擦特性随之改变,图7(c)为导轨滑块副水平垂直方向平均弹性力,查阅文献[15]得7 000~10 000 N的载荷作用下摩擦因数μ=0.004 3,将刚度与变形代入公式(10)中,求得4个滑块与导轨之间的摩擦力,工作台总摩擦力变化规律如图8所示。
工作台受到的摩擦力改变,从而改变进给系统受力情况,进给系统相位特性随之发生改变。
4 直线进给系统相位特性仿真分析
4.1 相位特性模型
基于Simulink,利用状态空间方法对进给系统动力学进行仿真,仿真模型如图9所示。
如图10所示,由伺服电机输入正弦激励信号,输入信号首次到达波峰时间为t0,输出信号首次到达波峰的时间为t1,相位角φ计算公式为
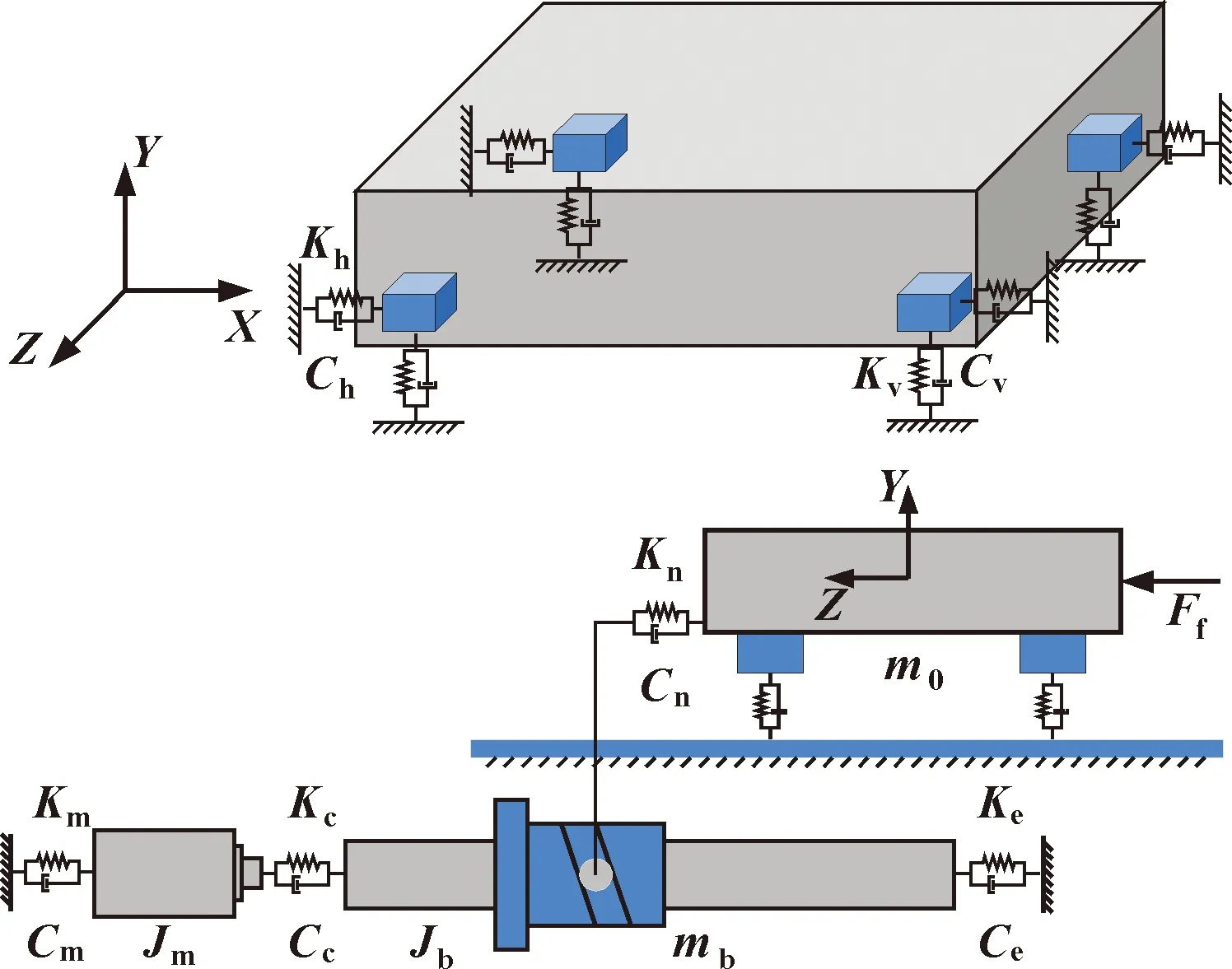
图1 进给系统简化模型
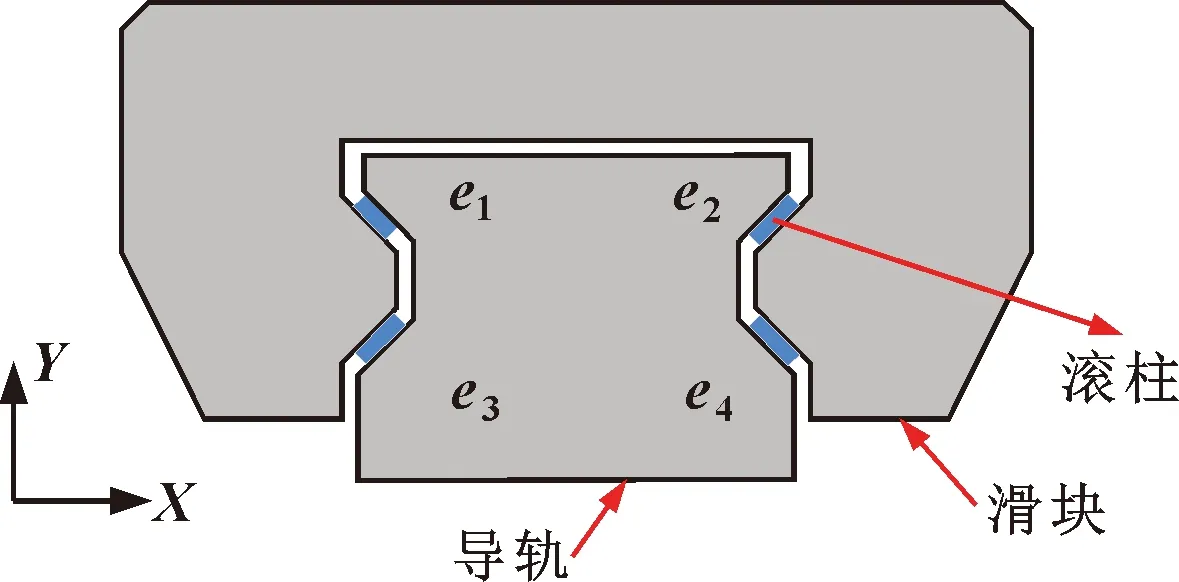
图2 导轨滑块副示意
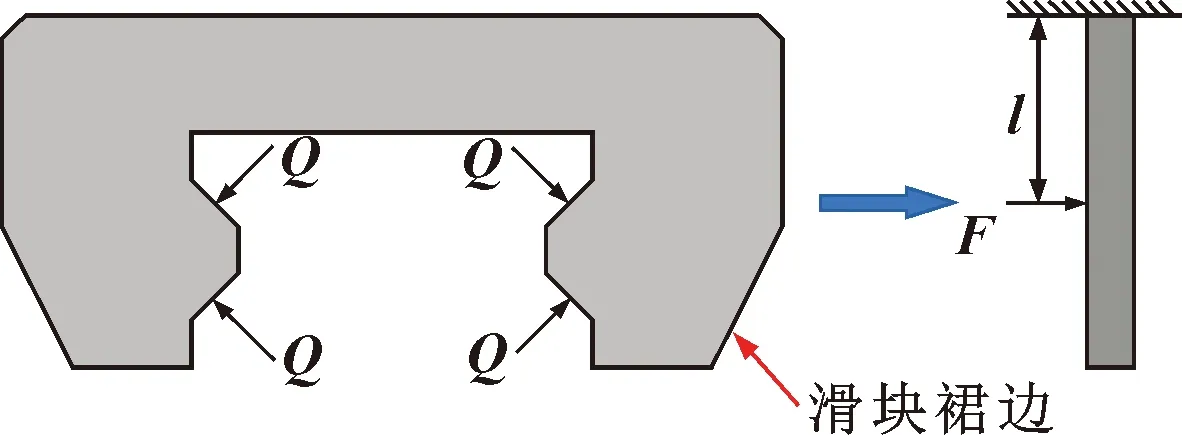
图3 滑块裙边等效示意
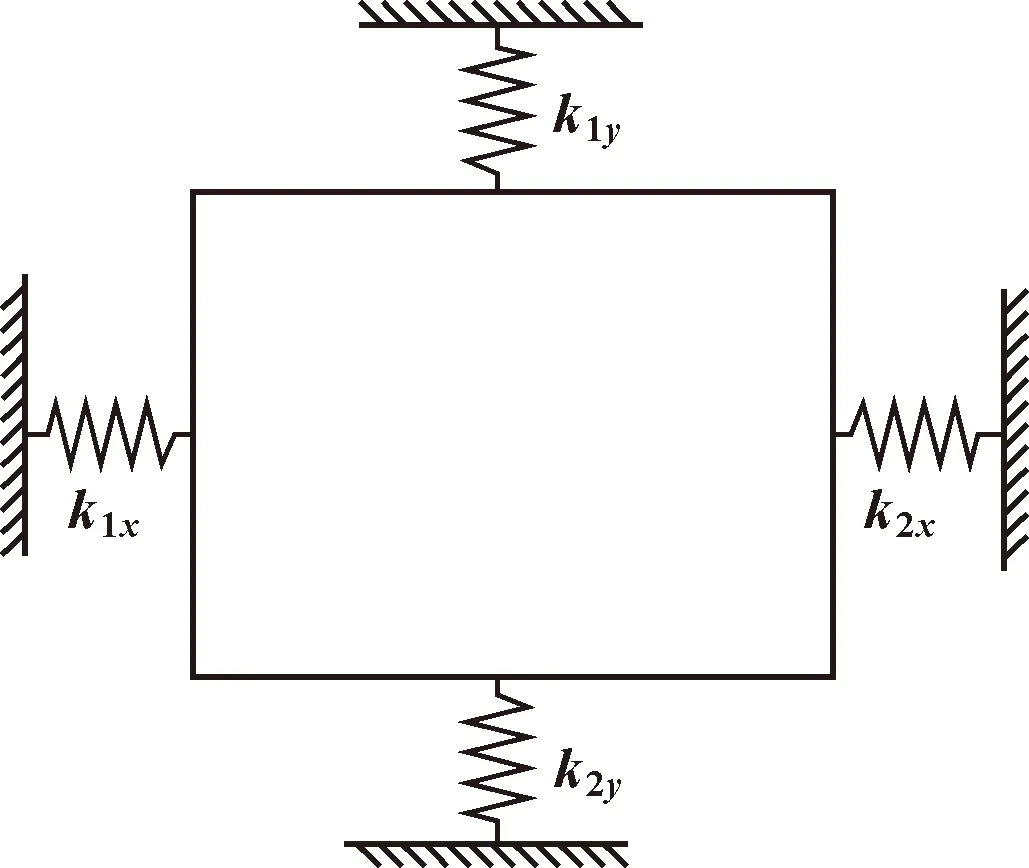
图4 导轨滑块副等效模型
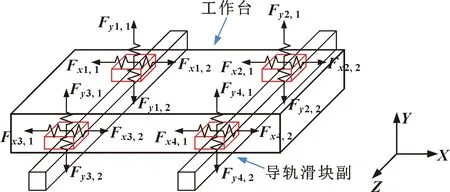
图5 工作台静力平衡模型

图6 导轨水平(a)与垂直(b)方向一侧存在拱形误差示意
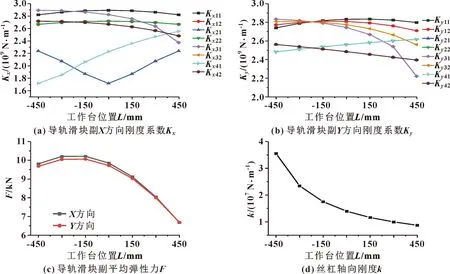
图7 不同工作台位置时进给系统内部参数
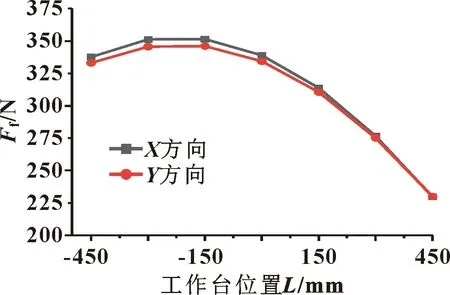
图8 工作台总摩擦力与位置关系
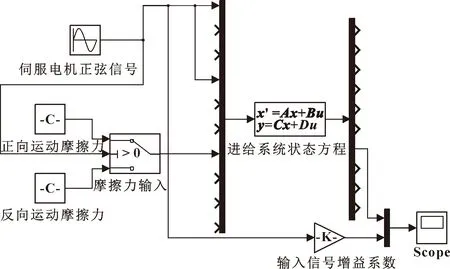
图9 Simulink仿真模型

图10 输入信号与输出信号对比
(14)
4.2 频率对相位特性影响
进给系统激振力频率由伺服电机转速决定,伺服电机的转速范围为0~1 800 r/min,因此保持其他参数不变,在转速范围对进给系统相位变化规律进行分析。具体工况为:X方向导轨误差e=0.01 μm,摩擦力由公式(10)计算可得Fc=334.38 N;Y方向导轨误差e=0.01 μm,摩擦力由公式(10)计算可得Fc=338.97 N。改变伺服电机转速,结果如图11所示。

图11 不同转速的相位特性曲线
由图11可得:伺服电机转速变化会改变进给系统相位特性,随着伺服电机转速增加,进给系统相位差逐渐增加。相位差小代表输出信号与输入信号之间延时小,进给系统有良好的跟随特性;相位差较大则代表工作台对输入信号的响应有一定滞后性,跟随特性较差。
当伺服电机转速在0~1 200 r/min之间时,输出信号与输入信号之间的相位差较小,且在1 200 r/min转速附近相位差趋近于零,输出信号对输如信号有着较好的跟踪特性。由于文中将摩擦力简化为固定值输入至系统当中,使得输出信号存在提前到达波峰的现象。而随着伺服电机转速的增加,1 200~1 800 r/min范围内进给系统机械特性当中的阻尼、摩擦等特性对系统影响逐渐显著,进给系统滞后的相位角有着较大的增加。1 800 r/min转速时,输出信号的相位差达到了28.12°,此时工作台对输入信号响应有着较大的滞后性。
综上可得:较低的转速时进给系统跟随特性较好;在高转速范围内,工作台输出端对伺服电机输入信号的响应存在一定的延时。因此,若使用轴间耦合技术对工作台移动的滞后特性进行补偿,可提高高速加工精度,需进一步进行相关研究。
4.3 摩擦力对相位特性影响
工作台摩擦力对进给系统相位特性也有一定的影响。保持输入信号频率不变,探究导轨存在拱形误差、工作台不同位置摩擦力变化时相位特性规律情况。具体工况为:伺服电机转速为1 800 r/min,保持其他参数不变,导轨X与Y方向分别存在拱形误差,不同位置摩擦力由图8可得。
由图12可得:工作台受到的摩擦力变化会对进给系统相位差产生影响。摩擦力越大,进给系统滞后的相位角增加。因此,高速高精度进给系统需对摩擦力进行相应的补偿,能进一步提高进给系统跟随特性。

图12 不同位置摩擦力变化的相位特性曲线
4.4 结合面参数对相位特性影响
大尺寸零件加工过程中,伺服电机转速不变,在此工况下进给系统输入信号频率保持不变,然而由于工作台位置变化较大,若导轨误差不同,不同位置下进给系统部分结合面参数会发生改变。具体工况为:伺服电机转速为1 800 r/min,平均摩擦力Fc=314.22 N,结合面参数由图7与表1可得。
由图13可得:丝杠轴向刚度变化对进给系统相位特性影响较大,导轨滑块副刚度变化对相位特性影响较小。由于丝杠刚度与工作台进给方向相同,系统对丝杠轴向刚度变化更敏感;而导轨滑块副刚度变化对相位特性影响较小,其弹性力的变化对进给系统影响体现在改变工作台摩擦力中,如图12所示。因此进给系统结合面参数变化会影响其相位特性,减小运动方向结合面参数的变化,能提高加工过程中动态特性的稳定性。
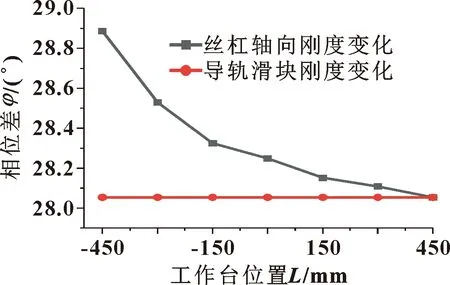
图13 不同位置刚度系数变化的相位特性曲线
5 结论
基于多轴耦合技术在多轴联动过程中,不同进给轴之间无法进行有效补偿的问题,对进给系统动态特性进行仿真分析,提出对工作台的输出端与伺服电机的输入端之间的响应滞后性进行量化,为多轴耦合提供参考。通过对进给系统相位特性进行分析,得到不同工况下进给系统相位变化规律,得出以下结论:
(1)由于工况不同,进给系统运行过程中动力学模型参数会发生改变。
(2)工作台受到的摩擦力增加,相位角越大,跟随特性越差,因此可通过摩擦力补偿提高动态特性。
(3)丝杠轴向刚度改变对相位特性影响较大,导轨滑块副刚度改变对相位特性影响较小,加工过程中保持关键动力学参数稳定,能有效提高动态特性。
(4)伺服电机转速变化对相位特性有着较大的影响,输入信号频率较低时相位差较小,进给系统跟随特性较好;转速较高时相位差增大,进给系统跟随特性较差。因此高速加工过程中进行轴间耦合时,可将相位差作为参数,补偿加工过程中的动态误差。

