基于改进粒子群算法的大件运输通行路径优化研究
方 鸿,吴 欣,郭伟奇,徐 凤
(1.湖南省交通科学研究院有限公司,湖南 长沙 410015;2.交通运输安全应急信息保障技术及设备交通运输行业研发中心(长沙),湖南 长沙 410015)
0 引言
近年来,随着我国经济建设的不断发展,大件运输车辆通行数量呈现出连年增高趋势。大件运输是指大型设备的运输配送工作,一般具有超限、超重、超几何尺寸等特点,由于大件运输的安全性与时效性具有深远的社会影响,部分专家学者对大件运输领域相关问题展开了研究。当前,关于大件运输的研究方向主要集中于两个方面,一是对大件运输车辆对桥梁承载能力的影响研究,钟杰等[1]以四川省大件运输桥梁可通行评估工作为工程依托,对普通公路大件运输的桥梁通行性评估体系进行系统分析与梳理;袁阳光等[2]同时考虑安全性与正常使用性能两方面要求建立了大件运输车辆过桥安全性评估方法,基于可靠度理论分析了桥梁构件的安全评估目标结果,实现了大件运输车辆可通行性的快速判定;高文博等[3]针对大件运输车辆通过斜拉桥时斜拉索钢绞线的强度退化问题,采用可靠度理论建立了斜拉索在大件运输车辆荷载下的两层次安全评估方法,可为大件运输荷载下的大跨桥梁构件安全评估提供相应的参考。此外,还有一些专家学者针对车辆荷载对桥梁的影响进行了评估[4-5]。二是对大件运输路径方案的选择研究,与常规的车辆路径规划问题不同,大件运输车辆路径优化既要考虑到线路的技术可通行性和经济因素,同时因为大件运输车辆具有可改装性,还需考虑在车辆参数变化情况下的可通行路径变化问题,故当前大件运输路线决策方案的相关研究,仍以定性的方法为主[6-7]。
根据现有研究总结可知,如何在保证桥梁结构安全的前提下合理地选择大件运输的最优路径,实现批量的大件运输车辆路径优化,是当前亟待解决的问题。基于此,本文以湖南省公路路网数据库和桥梁通行能力数据库为依托,创新性地提出一种大件运输车辆最优路径决策的优化模型,根据液压平板车可改装这一特点,将大件运输的路径优化问题转化为车辆轴重优化问题,实现可通行线路的重新匹配,以空间通行性、桥梁通行性、经济性和时效性为指标建立多目标优化模型,采用一种基于非线性惯性权重和动态学习因子改进的粒子群算法对车辆参数进行寻优分析,为公路大件运输通行路径优化问题提供一种新的解决方式。
1 问题描述
运输单位在对大件货物进行承运时,需要考虑运输的技术性影响因素及经济性影响因素,其中技术性影响因素不受经济性影响因素制约,是大件通行需要遵循的必要条件,对出发地至目的地间满足技术性条件的线路进行筛选后,余下的线路需要做技术性与经济性的分析,确保所选线路安全性最高,经济性最强,节约大件运输成本,故大件运输最优路线的决策问题,是一个典型的多目标优化问题。
1.1 影响因素分析
1.1.1技术因素分析
大件运输车辆在高速公路运输途中可能需要经过收费站、匝道、隧道、天桥、门架等存在多类几何限制条件的路线,这就要求大件运输车辆的车身几何参数需要满足该类设施的几何限制条件。令大件运输车辆的车身宽度为B,车身长度为L,车身高度为H,对于普通直线段公路则有:
(1)
式中:Wl为普通直线段上的公路宽度;Hb为高速公路上的障碍物高度,例如天桥、隧道、门架等。
弯道路段是高速公路互通或枢纽的常见路段,其通常以匝道形式出现在高速公路路网中,大件运输车辆在通过弯道路段时,如不能保证超长车身的扫空区域被包含于弯道区域内,则极易造成大件车辆或货物与弯道边界障碍物进行直接接触或碰撞,具有极大的安全隐患。此外,由于车辆过弯时会存在离心力,当车辆过弯的离心力大于车辆接地摩擦力时,会引起车辆侧翻,故大件运输车辆的弯道可通行性是大件车辆在运输路径选择中的重点技术性因素。为计算弯道可通行性数据,通常根据弯道经纬度数据获取连续的弯道边界,再使用Lagrange差值法对坐标进行插值拟合得到曲线函数,而大件运输车辆的扫空区则需通过车辆轮廓模型进行计算,如图1所示,根据文献[8]中的研究,给出大件运输车辆典型轮廓点A、I点的行驶坐标轨迹,计算公式分别如式(2)、式(3)所示。

图1 大件运输车辆转弯示意图
A点:
(2)
I点:
(3)
式中:(XA,YA)为A点的行驶轨迹坐标;V为大件运输车辆的行驶速度;Δt为车辆过弯时的瞬时取样时间;αA0为车头与Y轴正方向的夹角;αZ0为车头在Δt内转过的角度。
桥梁可通行性是大件运输车辆在高速公路上安全行驶的基本技术性条件之一,对于高速公路上的所有桥梁,利用有限元模型计算车辆荷载下的结构内力,并与桥梁承载能力进行对比,当大件车辆荷载下的结构内力小于桥梁最大承载能力时,允许车辆通过该座桥梁所在线路;当大件车辆荷载下的结构内力大于桥梁最大承载能力时,禁止车辆通过该座桥梁所在线路。综上,桥梁承载能力限制条件如式(4)所示:
Md<γMc
(4)
式中:Md为大件运输车辆荷载下的桥梁内力;Mc为通行路线上的桥梁承载能力,γ为桥梁承载能力安全储备系数。
以桥梁和枢纽为节点对高速公路路线进行分段划分,选取大件运输车辆空间可通行性和桥梁承载能力富余度作为技术性条件的目标函数,如式(5)所示。
(5)
式中:μ1、μ2、μ3为技术指标权重;n为该条公路上以桥梁为节点的分段数。
1.1.2经济因素分析
大件运输车辆的运输成本构成较为复杂,不仅包含燃油成本、改装车辆等基础运输费用,还包括运输时间、转运成本等间接运输费用,因此对于大件运输车辆运输经济性的最优选择需要同时考虑大件运输过程中的直接经济成本与时间成本,选取该两项因素建立经济性条件的目标函数[9],如式(6)所示。
(6)
式中:φ1、φ2为经济指标权重;tij为i、j城市间的运输时间;cij为i、j城市间的运输费用。
1.2 数学模型
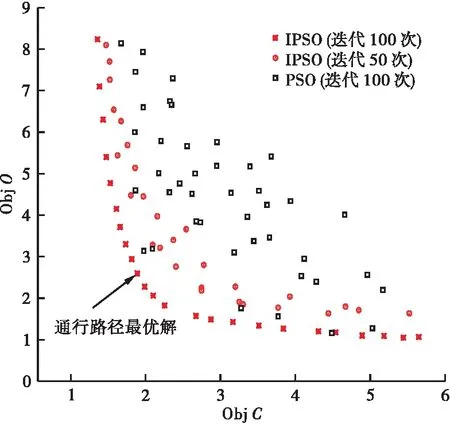
大件运输车辆通行路径优化问题不同于一般的路径优化问题,并非简单求解出发地与目的地之间的最短通行路径,而是根据大件运输车辆的超限性质,在考虑路线规划时应首先保证通行路径的技术性因素满足条件,同时,基于大件运输车辆的可改装性,液压平板车可以通过添加或减少轮轴的方式控制平板车的载货轴重。如图2所示,平板车减少轴数会导致轴重增加,此时P1>P2,由于桥梁承载能力的控制,部分线路上的桥梁无法通行要求,但减少轴数使得车身长度降低,线路的空间可通行性增强;反之,当平板车增加轴数使轴重减少时,P1 图2 大件运输车辆轴重分布图 故本文将大件运输车辆通行路径的优化问题转化为大件运输车辆参数优化问题,车辆申请参数的变化可改变各路径的可通行性,通过优化后的车辆参数信息重新匹配公路桥梁数据库中的通行路径,确定该优化后车辆申请参数的最优路径;此时,该优化问题为车辆参数的非线性优化模型。选取大件运输车辆液压平板车的轴重作为待优化参数,基于技术性指标和经济性指标,如式(7)所示构建大件运输车辆的路径选择的多目标数学优化模型,在保证空间和桥梁可通行性的前提下确定最优通行路径。 FindP min{O,C} s.t.Pmin≤P≤Pmax S>0 γMci>Mdi T≤Tmax C≤Cmax (7) 式中:P为行驶车辆待优化轴重;Pmin和Pmax分别为平板车轴重可变范围上下限;S为路线上的空间可通行性;T为运输时间;Tmax为运输单位申请的最大可接受通行时间;C为运输成本;Cmax为运输单位申请的可承受最大通行成本。 基于大件运输车辆路径优化问题的复杂性,车辆轴重进行增减动态变化时,相关技术性及经济性指标的变化趋势是非线性的;因此,本文采用粒子群算法对申请参数附近范围的最优参数进行随机搜索。粒子群算法是一种基于鸟类种群信息共享机制的进化计算技术,通过赋予粒子个体速度与位置属性,根据粒子之间的信息传递以更新每个粒子的速度方向,实现种群整体向搜索空间中最优解进行迁移。假设D维搜索空间中有粒子种群N,粒子群的标准更新公式如式(8)所示。 (8) 式中:vi ̄为粒子速度属性,决定粒子进化方向;xi为粒子位置属性,表明粒子当前在搜索空间中的位置;ω为惯性权重因子;c为学习因子;r为[0,1]上的随机数;pbi为个体极值;gbi为全局极值。 标准粒子群算法中惯性权重常采用线性递减策略,如式(9)所示。 (9) 式中:ω(t)为第t次迭代时的惯性权重值;ωmax、ωmin分别为惯性权重的最大、最小值;Tmax为最大迭代次数;T为当前迭代次数。 线性递减策略在遇到某些问题时易使算法陷入局部最优解,从而难以继续迭代收敛,为解决这一问题,平衡算法在全局空间和局部范围内的寻优能力,本文引入非线性惯性权重因子改善粒子群算法的寻优能力[10-11]。 (10) 学习因子作为粒子群算法中pbi和gbi的权重,可以控制粒子群的对个体最优解和全局最优解的记忆和学习能力,根据粒子群的搜索原理,为加快算法前期对搜索空间全局开发能力,同时保证算法后期侧重于局部精细化搜索,引入动态学习因子对原常数学习因子进行改进,动态学习因子的改进方式如式(11)所示[12]。 (11) 式中:cmax、cmin分别为学习因子的最大值和最小值。 为验证基于非线性惯性权重和动态学习因子改进的粒子群算法的寻优能力(Improved Particle Swarm optimization,IPSO),分别选取Sphere和Rastrigin函数对算法寻优性能进行测试,函数表达式如表1所示;算法仿真环境为Matlab2019a,种群规模取50,空间维度取30,最大迭代次数取500,为避免计算的偶然性,各算法均独立运行20次。同时,分别选取标准遗传算法(Genetic Algorithm,GA)、标准粒子群算法(Particle Swarm optimization,PSO)在同一环境下进行测试,以对比改进粒子群算法的寻优能力,遗传算法变异率Pm取0.5,交叉率Pc取0.7。算法测试结果如表2所示。 表1 基准测试函数 表2 测试结果 由表2可知,对于单峰测试函数Sphere,3种算法均有较好的收敛性,对于多峰测试函数Rastrigin,GA和PSO算法的寻优能力较差,在算法500次的迭代运算内未跳出局部极值,而基于非线性惯性权重和动态学习因子改进的粒子群算法仍可以跳出多峰测试函数的局部最优解,收敛至该测试函数的理论最优值附近。此外,对比20次寻优的平均耗时可知,改进粒子群算法在两种测试函数下的寻优速度均大幅优于GA和PSO算法,证明了改进策略的有效性。 为实现大件运输的最优路径决策,确保车辆轴重及轴距参数满足桥梁承载能力要求,采用Matlab编译优化程序,调用高速公路大件运输标准车型可通行性数据库进行可通行性验证,优化模型的基本设定流程如图3所示,基本执行步骤如下: 图3 算法执行流程图 a.初始化算法参数,令粒子种群数量为50,搜索空间维度D=30,最大迭代次数为100,根据车辆申请数据设定数学优化问题的约束条件。 b.评估当前个体最优解和全局最优解。 c.判断算法是否达到最大迭代,若达到则输出最优解,算法结束;若未达到,则进入步骤d。 d.根据式(8)更新非线性惯性权重,根据式(9)更新动态学习因子。 e.更新粒子适应度值。 f.返回步骤b重新确定种群个体最优解和全局最优解,并判断算法是否达到终止条件。 湖南省作为中南部地区的重点工业省份之一,大件运输许可申请数量连年递增。为解决大件运输车辆最优通行路径的决策问题,本文以湖南省大件运输智能审查系统、湖南省公路路网数据库和桥梁通行能力数据库为依托,基于改进粒子群算法的寻优模型,对算例中的车辆进行路径寻优,并验证该优化模型的可行性。 某大件运输车辆申请货物为塔筒,申请车辆类型为液压平板车,车货几何尺寸为:车货总长35 m,车货宽度4 m,车货高度4.5 m,车货总质量为135 t,轴荷分布为(10+20+7×15)t,平板车轴间距为1.2 m,申请起始收费站为A,终点收费站为B。由图4所示(虚线为非高速公路路段),根据路网数据库的分析结果,当前轴重下该车的可通行线路为G55-G72-G0421-G536。 图4 AB地简化路网示意图 采用Matlab将该车辆的申请信息编入优化程序,并调取公路路网数据库以匹配可通行线路,分别采用标准粒子群算法和改进粒子群算法对车辆轴重进行寻优分析,并匹配最优轴重下的通行路径,该问题的Pareto前沿分布如图5所示。 图5 Pareto前沿分布 由图5可知,改进粒子群算法对该大件车辆轴重优化下的路径决策问题具有更好的适应性。改进粒子群算法可以完成较快速度的迭代收敛,有效跳出局部最优解,种群在有效迭代次数内迅速收敛至Pareto前沿,而标准粒子群算法种群则无法完成搜索寻优,100次迭代后仍未到达Pareto前沿。根据粒子群寻优结果,当平板车轴重为11.67 t时,车辆可以行驶G55-G72-G0422线路抵达目的地,此时平板车轴数增加至9轴,长度增加至37.4 m。 图6给出了新运输路线与运输路线的技术经济指标相对变化率,由图6可知,新线路桥梁承载能力平均富余度相对原线路下降了4.8%,空间通行能力富余度下降4.6%,说明新线路桥梁承载能力低于原线路,由于车长的增加,线路的空间富余度也出现一定程度的下降,而由于新线路高速路段更长,大件运输时间节省15.7%,经济成本降低10.4%,有效提高了大件运输车辆运输效率。相较于原通行线路,新线路在充分利用公路资源,保障运输安全的前提下节省了运输成本,提高了大件运输的经济效益,说明了该优化模型的可行性。 图6 评价指标相对变化率 本文为解决大件运输车辆最优通行路径决策问题,基于一种非线性惯性权重和动态学习因子的改进粒子群算法,依托公路路网数据库,将大件运输路径优化问题转化为路网数据下的轴重寻优及路线匹配问题,得到结论如下: a.大件运输车辆申请起始地与目的地之间的最优通行路径决策问题可以转化为依托路网数据库下的最优轴重确定问题,通过改变平板车轴数以调整轴重的方式可以在保证线路桥梁承载能力、空间通行能力等技术性指标的同时匹配路网数据库中技术性及经济性最优的通行路径。 b.基于非线性惯性权重和动态学习因子改进的粒子群算法相较于标准粒子群算法寻优能力得到了大幅提升,对于大件运输最优通行路径决策问题具有良好的适应性。 d.优化后的大件运输通行线路相较于原通行线路实现了公路通行能力资源的高度利用,降低了运输成本,提高了大件运输的经济效益。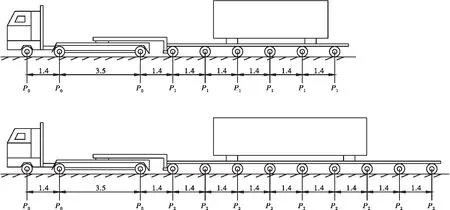
2 基于非线性惯性权重和动态学习因子的粒子群算法
2.1 标准粒子群算法
2.2 非线性惯性权重因子和动态学习因子


2.3 算法性能验证


2.4 优化模型设计

3 案例分析


4 结论

