隧道开挖致使土层缺失对桩基稳定性影响研究

王 真，陈双庆 ，王吉平

(1.湖南省交通科学研究院有限公司，湖南 长沙 410015；2.交通建设工程湖南省重点实验室，湖南 长沙 410015；3.中南大学 土木工程学院，湖南 长沙 410014)

1 概述

随着我国城市基础建设的快速发展，为缩短运行距离及缓解交通压力便利出行，城市地铁建设发展迅速；而新建地铁隧道开挖施工导致的地层缺失将不可避免地对周围岩土层造成一定程度的扰动，使隧道地层发生位移变形，进而影响邻近地表建筑物、路面结构、地下管线及桥梁桩基的正常使用和结构安全，严重时会造成地面塌陷甚至出现桥梁失稳等重大事故[1-3]。由此可见，地铁隧道开挖致使地层缺失引发的工程灾害问题不容忽视，因此对隧道开挖过程中各影响因素及其稳定性开展研究，对隧道设计、施工有积极的指导意义。

近年来国内外已有许多学者通过理论、数值计算及现场监测对隧道开挖桩基稳定性问题展开研究。如康庄等[4]引入角度系数对Peck公式进行修正，并利用动力学仿真分析研究不同斜交角度所产生的不同沉降形式对脱轨系数及减载率的影响。林存刚等[5]基于虚拟镜像技术，推导了在隧道土层不同收敛模式下的地面沉降计算公式，该算法高估了横向地面沉降槽宽度。SAGASETA等[6]基于镜像法原理，考虑地层损失推导了应变场弹性半空间解析解。魏其涛、梁发云等[7-8]分别基于Poulos两阶段法，提出了考虑土体侧移和既有轴向荷载耦合作用近似单桩的简化计算方法。DING等[9]基于弹性半空间理论，求解了扰动荷载作用下，盾构施工引起邻近建筑物的地表沉降。孙宇坤等[10]通过杭州地铁某区间隧道工程，发现砌体结构建筑物后续沉降阶段的下沉量占累积沉降量的比例明显大于天然地表。邓崴等[11]通过对广州地铁二号线盾构隧道工程中砂黏互层地层的横向沉降监测，根据现有的沉降槽宽度系数预测理论，提出了更适合砂黏互层地层沉降槽沉降系数的计算方法。袁孝蓓等[12]通过对南京地铁四号线某盾构施工期间现场实测数据进行Peck公式拟合，分析了典型沉降槽曲线特征，获得了不同地貌单元的沉降槽形状特征及沉降槽宽度参数经验值，并对不同地质条件沉降影响范围作出了预测。可见，现有研究对于隧道开挖致使地层缺失引发的邻近桩基失稳及其桩土相互作用机理并不明确，同时地层缺失对邻近桩基的内力与位移影响问题理论研究较少。

鉴于此，本文拟考虑隧道开挖下土体自由场位移，并根据地基反力系数法及桩侧水平向荷载传递机理，建立了桩基受力变形简化计算模型，并通过有限差分法和增量法对桩身内力和位移进行求解，最后探讨了桩径、桩-隧相对距离等因素对桩基受力变形的影响，以期为类似隧道工程设计提供参考。

2 隧道开挖下邻近基桩非线性分析

2.1 隧道开挖桩周土位移场模型

隧道开挖必定会对基桩附近土层产生扰动，使得土层位移场发生改变，进而对邻近桩基稳定性产生不利影响，因此土层自由位移场对桩基的影响可简化为如图1所示。由隧道开挖引起的桩-土相互作用问题，基于Winkler理论作如下假定：桩基为弹性体；岩土体为理想弹塑性连续变形体；桩-土之间不发生滑移，且始终保持弹性接触。

图1 土层自由位移场对桩基的影响示意图

由于隧道开挖对土层位移场的影响并不明确，因此分两步对该问题进行分析，第一步是估算隧道开挖施工时桩周土层自由位移场大小，第二步是在第一步计算的基础上，进一步考虑土层缺失对基桩受力与变形的影响。对于隧道开挖土层自由位移场的估算，采用LOGANANTHAN等[13]提出的修正解析方法进行计算，其表达式为：

(1)

(2)

式中：Δs(z)为桩周土层任意点竖向位移；ωs(z)为桩周土层任意点水平位移；x为土体与隧道轴线的距离；z为地面到土层中计算点的深度；h为隧道轴线埋深；νs为土体泊松比；ε0为等效地层损失比，表达式为：

(3)

式中：g为间隙参数；R为隧道半径。

2.2 桩侧水平向荷载传递模型

由2.1节得到隧道开挖土层自由位移场解答，桩基水平承载特性的变化主要是土层缺失导致桩周土体水平抗力减弱，进而引发桩基水平向稳定性问题。在此基础上，可采用地基反力系数法来考虑土体扰动产生的自由位移场对邻近桩基水平向受力变形的影响，桩身水平向荷载传递模型选取KONDNER[14]和GOH等[15]推荐的双曲线形式，其桩侧土抗力与桩土水平相对位移的表达式：

(4)

式中：p(z)为桩侧土抗力；ωp(z)为深度z处桩基水平位移；Rf为破坏比，一般取值为1.0；pu(z)为桩周土极限抗力，根据不同土体类型取值不同，黏性土计算式为：pu(z)=(3+γz/cu+0.25z/r0)cu，砂土计算式为：pu(z)=3γz(1+sinφ)/(1-sinφ)，γ为土体平均重度，cu为土体不排水抗剪强度；kni为土体初始地基反力系数，可由式(4)确定：

(5)

式中：r0为桩基半径；Ei为土体弹性模量；EPIP为桩基抗弯刚度。

2.3 桩身内力位移计算的理论解答

为建立基桩水平向受力变形基本方程，根据Winkler弹性地基梁理论，可知地面上某点沉降y与底部压力p成正比，即p=ky，式中k为弹性地基基床系数。并对模型进行一些假定：忽略桩身轴力对基桩内力与位移的影响，只考虑桩身水平向的受力和变形。基桩简化计算模型，如图2所示。

图2 桩基简化计算模型

图2中，桩基长为Lp，桩顶受竖向荷载P0、横向荷载和H0，以及弯矩M0组合作用，桩侧土提供土抗力来平衡外荷载。为方便求解计算，以桩顶轴心为原点建立基桩微元段yOz坐标系，其微元段受力分析示意图，如图3所示。

图3 桩基微元段示意图

根据图3取桩身微元段进行受力平衡分析，略去高次微分项，并求导即可建立该桩段的挠曲微分方程：

(6)

根据材料力学可知，M和dH/dz分别可表示为：

(7)

(8)

将式(7)和式(8)代入到式(6)中，并且由于主要考虑桩基水平向变形，因此忽略竖向荷载P对桩基的作用，由此方程可简化为：

(9)

由2.2节所得桩侧土抗力式(4)代入式(8)中，可得考虑土层缺失影响的桩身挠曲微分方程：

(10)

根据桩身受力及桩基刚度等情况，将桩身等分为n段，每段长为l，桩身节点号为0，1，…，N。同时为方便差分法求解，特在桩基顶部和底部分别增加2个虚拟桩段，其节点编号分别为：-2、-1和N+1、N+2，桩基挠曲及桩身差分示意，如图4所示。

图4 桩身挠曲及其差分点

基于差分法原理，将差分代替微分可得第i桩段的差分格式为：

(11)

式中：ωp，i为第i桩段的挠曲值；ωs，i为第i桩段桩周自由场土体的水平位移；pu，i为第i桩段桩周土体水平抗力。

桩顶和桩端的边界条件由差分格式分别给出。

(12)

(13)

每个相邻桩段必须满足相应的协调条件，如桩段位移、转角、弯矩和剪力都满足相等关系，其对应的差分格式为：

(14)

由于方程组为非线性，而式(11)右侧不能直接化简为矩阵模式，不便于计算求解，因此引入增量法[15]对方程进行求解。

假设μ=ωs(z)-ωp(z)，即μi=ωs，i-ωp，i，由此将式(10)化为增量形式为：

[Kp]{Δωp，i}=[Ks]{Δμi}=

[Ks]{Δωs，i-Δωp，i}

(15)

式中，{Δωp，i}为第i桩段水平位移增量列向量；{Δωs，i}为第i桩段处桩周自由场土体位移增量列向量；[Kp]为桩身水平刚度矩阵；[Ks]为桩侧土弹簧刚度矩阵。

(16)

[Ks]=2r0×

(17)

据此可通过增量法求解方程，首先根据土体缺失产生的土体自由场确定土体位移向量；然后通过编制相应matlab计算程序求解桩身水平位移及桩土相对位移；最后通过桩身水平变形换算得到桩身内力。

3 试验对比及影响因素分析

3.1 与现场实测情况对比

LEE等[16]对英国伦敦某隧道开挖致使桩基位移进行监测，实际工程中隧道下穿建筑时为群桩基础，但现有研究发现隧道开挖对群桩侧向影响并不明显[17]，因此本文为简化计算将只考虑隧道开挖对单桩的影响。隧道与桩基距离为5.7 m，开挖隧道在地表下15 m左右，桩基长为28 m，桩径1.2 m，弹性模型30 GPa，黏土不排水抗剪强度50～200 kPa，由桩顶至桩底呈线性增大。隧道及其邻近桩基相对位置，如图5所示。

图5 隧道及邻近桩基位置示意图

根据图5所示，通过计算分别得到第一阶段开挖导洞和第二阶段开挖扩大洞时桩身水平位移，以及开挖完成后桩基最终水平位移。计算值与实测结果对比，如图6所示。

图6 桩身水平位移实测与计算结果对比图

通过图6可以发现，随着隧道开挖桩身水平位移沿深度逐渐增加，当接近隧道水平轴线时，桩身水平位移达到峰值，并且现场实测结果和理论计算值变化趋势基本吻合，桩身最终位移理论计算值略大于实测值，结果偏保守。计算阶段1开挖导洞时桩身位移较小，当开挖到阶段2扩大洞时桩身水平位移较阶段1大幅增加，可见土体自由场位移对桩身位移的影响较大，因此在实际隧道工程开挖后未支撑阶段为最危险工况应加强监测。

3.2 桩身水平承载特性影响因素分析

隧道开挖致使对桩基水平承载特性的影响因素众多，于此本文仅以3.1节中伦敦地铁第二阶段开挖扩大洞后桩基变形情况为例，分别对桩径大小及桩-隧相对位置等因素进行分析计算，探讨其变化对桩基内力与位移的影响。

3.2.1桩径的影响

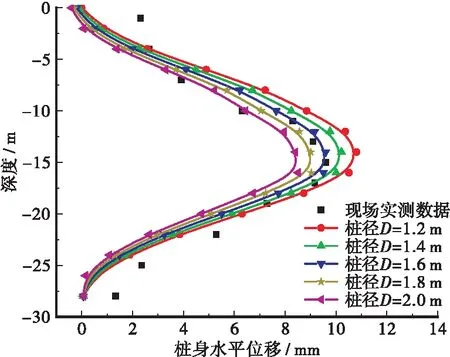
为了探讨隧道开挖工况下，不同桩径变化对桩基水平承载特性的影响，通过计算得到了桩身水平位移和桩身弯矩随桩径D(1.2、1.4、1.6、1.8、2.0 m)增大的变化曲线，如图7(a)和图7(b)所示。

(a)桩身水平位移变化曲线

图7(a)和图7(b)是随着桩径增大、隧道开挖对桩基水平位移以及弯矩的影响曲线。由图7(a)可知，当桩径D分别为1.2、1.4、1.6、1.8和2.0 m时，对应桩身最大位移分别为10.81、10.22、9.61、9.03、8.51 mm，桩径由1.2 m增大至2.0 m时，桩身最大水平位移减幅为21.3%；随桩径增大桩身水平位移逐渐减小，曲线变化趋势基本一致。同样地，通过图7(b)发现，桩身最大弯矩随着桩径增加呈非线性增大。对比各个工况，在同一条件下，桩径越大，隧道开挖对桩基水平位移的影响较小，而对弯矩影响较大，这是由于桩径增大会使得桩身抗弯刚度变大，其抵抗变形的能力增加，导致桩身水平位移变小，进而使得桩基承受的弯矩变大。由此可知，增大桩径可在一定程度内减小桩基水平变形，继续增大桩径对改善基桩水平位移的效果有限，反而会增加施工成本，因此建议在兼顾安全性和经济性的同时，可对桩基设计进行优化。

3.2.2桩基-隧道相对水平间距的影响

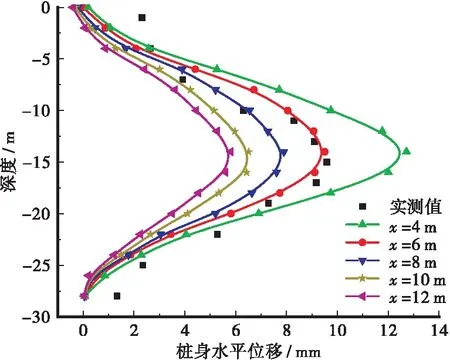
为考虑隧道与桩基的相对距离对桩基稳定性影响，在保证其他条件不变，分别取桩-隧相对间距x为4、6、8、10、12 m时，桩身水平位移及桩身弯矩变化曲线，如图8(a)和图8(b)所示。

(a)桩身水平位移变化曲线

通过图8(a)和图8(b)可以发现，桩基与隧道相对距离越大、隧道开挖对桩身水平位移和弯矩的影响越小，说明随开挖距离增加，由卸荷引起的土体侧移对桩基承载性能的影响较小。当隧道中轴线距离桩基越近，对桩基水平承载的影响最大，桩身水平位移和弯矩均越大，曲线出现峰值点，其变形峰值位于隧道中轴线处深度15 m左右。当桩-隧相对距离x分别为4、6、8、10、12 m时，对应桩身最大位移分别为12.72、9.51、7.92、6.51、5.81 mm，最大弯矩值分别为105.22、63.91、33.49、14.91、4.26 kN·m；桩-隧相对距离x由4 m增大至12 m时，桩身最大水平位移减幅为54.3%，桩身最大弯矩减幅为96.0%。相较于桩径变化，桩-隧相对距离对桩基的影响更大，这表明当隧道下穿既有建筑物时，应明确是否有建筑桩基，同时应探明桩基位置、数量，尽量避开或远离桩基，减少因隧道开挖对邻近桩基稳定性的影响。

隧道开挖不可避免地会对周围建筑物基础产生影响，通过本文研究成果可在理论方面对隧道开挖引起的桩基受力特性进行计算，可初步对桩基稳定性进行评估。鉴于现在城市地铁隧道建设的持续推进，基于本文方法计算结果，可评价城市隧道开挖对邻近建筑物桩基的影响，并制定切实可行的防控措施，有重大实践意义及广泛的应用前景。

4 结论

本文基于理论方法研究了隧道开挖对邻近桩基水平向承载特性的影响，并对桩径、桩-隧相对距离等参数展开影响因素分析，得到如下主要结论：

a.通过考虑土体自由场位移及桩身水平荷载传递机理，建立了桩基内力位移简化计算模型，并通过有限差分法和增量法进行求解，对比分析发现理论值与现场实测数据较为吻合，验证了理论计算模型的合理性。

b.桩身弯矩随桩径增大而增加，而桩身水平位移呈非线性减小，桩径由1.2 m增大至2.0 m，桩身最大水平位移减幅为21.3%；增大桩径可一定程度提高桩身水平承载能力，而减小桩身位移。

c.随桩-隧相对距离增加，桩身位移和弯矩均减小，由4 m增大至12 m时，桩身最大水平位移减幅为54.3%，桩身最大弯矩减幅为96.0%；隧道中轴线距离桩基越近，桩身水平位移和弯矩均越大；相较于桩径，桩-隧相对距离变化对桩基的稳定性影响更大。

在缺少现场实测数据和试验资料的情况下，上述结论可为城市隧道开挖及邻近建筑物桩基设计提供参考。鉴于理论计算进行了理想化的假定和简化，忽略了实际工程复杂的环境因素影响，进而导致计算结果与实际工程监测结果有一定误差，理论计算结果虽能反映一些定性的规律，但仍需继续开展更多的现场试验研究工作，以期对理论模型进行修正和完善。