沥青加铺层反射裂缝动应力强度因子分析

黄钦寿，陈晋平，曾威凯，孟勇军

(1.广西交通设计集团有限公司，广西 南宁 530029；2.广西大学 土木建筑工程学院，广西 南宁 530004)

0 引言

大量城市周边高速公路或一级公路随着城市快速发展不断提升改扩建为城市快速路，当前水泥混凝土路面改扩建项目广泛应用方案为加铺沥青面层。但由于旧路水泥板接缝存在，在沥青面层极易形成反射裂缝，缩短路面寿命，国内外学者围绕反射裂缝扩展原理开展深度分析。王金昌等[1-2]、黄志义等[3]基于动力学理论和平面应变有限单元法,探讨车辆动荷载作用下道路结构参数和地基参数改变下动应力强度因子变化规律及对道路结构工作特性影响。蒋建群等[4]深度分析黏弹性地基在动荷载作用下所产生相关稳态响应机制。罗辉等[5]基于结构动力学相关理论,探讨多层沥青路面响应机制。苗雨等[6]结合动力学理论分析含裂缝沥青路面动力学信息。张程[7]建立车辆通过减速带路面冲击荷载作用数值模型,研究冲击荷载作用沥青加铺结构参数敏感性。胡蓝心[8]综合线弹性断裂力学等理论开展分析,建立不同结构参数旧水泥混凝土沥青加铺层三维模型,分析计算加铺层结构在单独车辆荷载作用及温度-荷载耦合作用下力学响应。

本文在现有研究成果基础上，以南宁现有高速公路东环改造二期工程典型沥青加铺层为例开展分析，结合动力学和断裂力学理论，采用有限元法围绕沥青加铺层动应力强度因子开展分析，研究了行驶速度、轴载、裂缝长度、路面结构层材料和接缝宽度变化下动应力强度因子伴随时间的变化规律。

1 基本理论

1.1 动力学基本理论[9]

运用有限单元法开展车辆载荷指标分析，对于路面的控制方程[9]为式(1)与式(2)：

(1)

C=αM+βK

(2)

(3)

式中：w1为基本圆频率；ζ1为阻尼比。

1.2 动态应力强度因子KI(t,θ)的确定[2]

裂尖附近坐标示意图见图1，含反射裂缝路面结构图见图2。裂尖附近位移场表达式[2]为式(4)。

图1 裂尖附近坐标示意图

图2 含反射裂缝路面结构图

(4)

式中：u(t，θ)和ν(t，θ)分别为沿x轴方向的位移、沿y轴方向的位移；s=3-4μ；μ为泊松比。令α=180°，获得垂直反射裂缝面位移表达的具体因子表达式[2]，见式(5)：

(5)

(6)

对式(6)取极限[2]，可得式(7)：

(7)

确定奇异单元上J、N节点具体竖向位移参数，通过式(7)确定出A(t，θ)，再由式(6)、式(7)确定出KI(t，θ)。由以上分析可知KI(t，θ)是一个由动位移场唯一确定的导出参量。

2 分析模型和荷载场

2.1 分析模型的简化

顺着行车方位构建应变计算模型，有限元计算模型见图3，反射裂缝尖端附近网格划分见图4，沥青加铺层结构计算图见图5，路面建成后现场图见图6，计算参数见表1，其中阻尼矩阵系数的取值见文献[10]。

表1 主要计算参数

图3 计算模型

图4 裂缝网格划分图

图5 沥青加铺层结构计算图

图6 路面建成后现场图

沥青混凝土动态性质的主要影响因素为车辆荷载、温度变化和作用时间等，选择20 ℃情况下具体的动态模量参数[11]展开分析。多种加载频率下计算得出的动态模量参数详见表2[12]。

表2 不同加载频率的动态模量(0.7 MPa,20 ℃)[10]

表2仅介绍4种加载频率情况下具体的动态模量参数，通过针对性的回归研究得出动态模量和加载频率存在较为优秀的幂乘关系，见图7。加载周期和频率之间存在特殊的倒数联系，通过公式换算处理得出混凝土和加载周期的关系式，详见式(8)：

图7 沥青加铺层动态模量与加载频率的关系

(8)

式中：MA和T分别为沥青混凝土动态模量、加载周期。

2.2 荷载场的确定

荷载选用车辆标准轴载BZZ-100[11]，接地压力0.7 MPa[11]，荷载变化规律的具体参数选择Kenlayer简化方案[13]，为对称作用于沥青加铺层反射裂缝正上方的正弦分布荷载,见图2和式(9)。

(9)

式中：T为荷载的作用时间；L为轮胎的接触面积半径(15 cm)；V为行驶速度。转换荷载作用时间至[0，T]区间得出式(10)：

(10)

结合式(10)可以获得多种车速的具体荷载时间,再结合式(8)可获得多种车速的动态模量值，具体信息详见表3。不同车速荷载强度随时间变化图见图8。半周期动态荷载参数详见表4。

表3 不同车速下荷载作用时间与动态模量

表4 动态荷载半周期变化值

图8 不同车速荷载强度随时间变化图

3 参数变化对动应力强度因子的影响

计算参数分别为：车速、车辆轴载、反射裂缝长度、路面结构层厚度或模量、旧水泥混凝土板接缝宽度。

3.1 车速变化对KI(t,θ)的影响

车辆行驶速度从40 km/h递增至120 km/h，逐级增幅为20 km/h，具体的计算结果见图9。

(a)1 cm裂缝长度

图9为不同车速在裂缝扩展3个不同时期所对应的动态应力强度因子随时间变化结果。结合图9所述的数据能够发现，动应力强度因子伴随时间表现为周期性转变，KI峰值参数伴随车速的不断提升而不断下降。对于裂缝扩展的初、中、后期，120 km/h与40 km/h的KI峰值参数进行对比降幅分别为24.3%、6.5%与3.9%。结合数据对比能够得出，车速的提高有利于延缓裂缝的扩展，但实际运营中存在大量的超载和车速较低的车辆，加速裂缝的扩展。图9(d)为车速对最大动态应力强度因子影响分析图，伴随速度的提升最大动态应力强度因子数值不断降低。取1 cm长度为例，选择速度40 km/h和120 km/h进行对比，数值由0.128 MPa·m1/2降低至0.097 MPa·m1/2，降幅为24.3%。研究得出车速较高的情况下，对于裂缝扩展所构成的影响相对较小。

图10为正则化Kr(动/静应力强度因子)在裂缝扩展1 cm时多种车速作用下最大动/静应力强度因子的变化曲线。结合图10数据能够发现，动态荷载对Kr所产生的影响与静态荷载影响原理有所区别，这也是和车速复杂特征有关。Kr的峰值在车速小于90 km/h时超过了对应的静态应力强度因子；Kr峰值参数在车速超过90 km/h时低于静态因子，结合图示信息能够发现高速行驶对裂缝扩展所构成的影响小于低速行驶。数值伴随车速提升而不断降低。动应力强度因子在速度提升至90 km/h时低于静应力强度因子，结合图10中得出提高车速有助于减少动应力强度因子。

图10 正则化I型动/静应力强度因子曲线

3.2 车辆轴载变化对KI(t,θ)的影响

固定车速80 km/h，车辆轴载由100 kN递增到240 kN，逐级增幅为20 kN，具体的计算结果数据见图11。

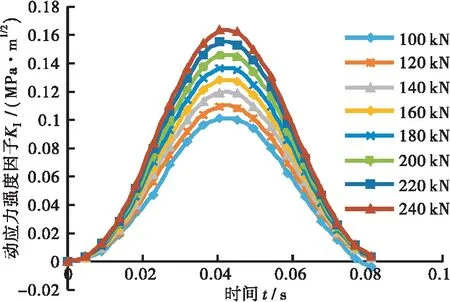
(a)1 cm裂缝长度

由图11可知，动应力因子在轴载影响下的变化特征和外部荷载函数具有相近性。裂缝扩展3个不同时期的动力响应参数伴随轴载参数的增加不断增大。1、4、8 cm裂缝对应的强度因子在轴载从100 kN提升到240 kN时，分别从0.100 8、0.280 7、0.709 8 MPa·m1/2增加到0.162 7、0.489 4、1.209 0 MPa·m1/2，增幅分别为61.4%、74.3%、70.3%。结合图11信息得知轴载对于裂缝扩展的影响较大，在实际运输过程中应当加强管控超重车辆，减缓裂缝的快速扩展。图11(d)为轴载对最大动态应力强度因子影响图。选取4 cm长度为例,动应力强度因子在轴载从100 kN提升到200 kN时,数值由0.280 7 MPa·m1/2大幅度提升到0.442 0 MPa·m1/2，增大57.5%，表明了轴载的提升会加快裂缝的扩展。

3.3 反射裂缝长度变化对KI(t,θ)的影响

反射裂缝长度由1 cm增加到8 cm,采取1 cm逐级递增,固定车速为80 km/h,计算结果见图12。

(a)不同裂缝长度

从图12可知，动应力强度因子曲线伴随裂缝长度的提升而不断向上突起，这种趋势随着裂缝长度的增加增幅越来越大。当长度从1 cm增长至2 cm时，强度因子增加0.035 MPa·m1/2，增长比例为34.8%；当长度从5 cm增长至6 cm时，强度因子增幅为0.152 MPa·m1/2，增长比例为42.8%。图12(b)为不同裂缝长度下最大动/静应力强度因子变化曲线，动荷载数值相对于静荷载数值显著偏大，两者插值伴随裂缝的不断增长而不断增大，裂缝长度为1 cm时差值为0.035 MPa·m1/2，裂缝长度为8 cm时差值为0.139 MPa·m1/2。研究得出扩展相同的裂缝长度可承受的荷载次数伴随裂缝的扩展而不断减少。

3.4 路面结构层参数变化对KI(t,θ)的影响

保持车速为80 km/h不变，只改变沥青加铺层、应力吸收层厚度或模量中一个材料参数计算动应力强度因子，计算参数见表1。

3.4.1沥青加铺层厚度变化对KI(t,θ)的影响

取沥青加铺层厚度9 cm，从10 cm逐级递增2 cm到20 cm进行分析。计算结果见图13。

(a)1 cm裂缝长度

从图13得出反射裂缝扩展3个阶段动应力强度因子随加铺层厚度变化的曲线图。KI峰值随加铺厚度的增加而不断降低。取1 cm长度为例，选择厚度9 cm和20 cm数值进行对比，KI由0.101 MPa·m1/2减小到0.025 MPa·m1/2，减幅为75.2%。而且从图13所述的数据能够得出，动应力数值伴随厚度的增加非线性递减。选取4 cm长度为例，面层厚度由10 cm提升至14 cm时动应力强度因子减幅38.2%，面层厚度由14 cm提升至18 cm时动应力强度因子降幅29.2%。综合研究得出厚度提升会降低动应力强度因子，若是单纯依靠提升厚度延缓反射裂缝的扩展并不理想。

3.4.2沥青加铺层动态模量变化对KI(t,θ)影响

沥青加铺层动态模量由800 MPa递增至2 400 MPa，逐级增幅为200 MPa，计算结果见图14。

(a)1 cm裂缝长度

从图14可以看出，动应力强度因子变化曲线与动荷载变化曲线相似，动应力强度因子数值伴随模量的提升不断下降，扩展后期模量变化产生的影响最为显著。选择800 MPa和2 400 MPa数值进行对比，1、4与8 cm裂缝尖端强度因子降幅分别为62.9%，52.6%和36.9%。结合图14(d)能够发现强度因子的降幅趋势不断减缓，选择1 cm裂缝为例，取800 MPa和1 600 MPa数值进行对比，模量的提升数值降幅为43.0%；取1 600 MPa和2 400 MPa数值进行对比，模量的提升数值减幅为32.2%。研究得出加铺层模量的提升可有助于降低反射裂缝的扩展，对模量选取应当结合多个因素进行综合考虑。

3.4.3应力吸收层厚度变化对KI(t,θ)的影响

应力吸收层厚度由1 cm递增至4 cm，逐级增幅为0.5 cm，计算结果见图15。

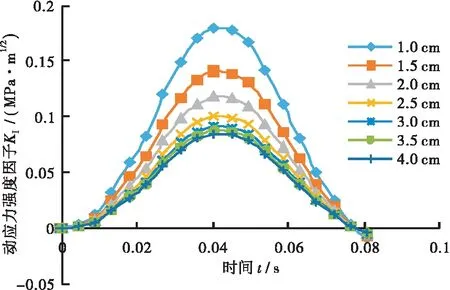
(a)1 cm裂缝长度

从图15得出应力强度因子的变化曲线伴随层厚提升而不断减缓。如4 cm裂缝在厚度从最初的1.5 cm提升至2.5 cm的时最大KI值的减幅为28.5%，从3 cm提升至4 cm时降低幅值为7.6%。结合图15所示信息可得出适度的应力吸收层厚是必要的，但过厚的吸收层厚度无法实现很好的减弱效果又浪费资源。

3.4.4应力吸收层弹性模量变化对KI(t,θ)影响

应力吸收层模量由400 MPa递增至1 600 MPa，逐级增幅为200 MPa。计算结果见图16。

(a)1 cm裂缝长度

图16为吸收层模量与动应力强度因子关系图。

结合图16所述的数据能够发现，动应力强度因子的变化曲线随着吸收层模量的增加而不断向下变化，但变动幅度相对较小。选择400 MPa和1 600 MPa数值进行对比，1、4与8 cm裂缝的最高KI值随着模量的提升降低幅度分别为4.6%、4.8%以及7.4%。分析可知吸收层模量的提高可降低强度因子数值，但所构成的影响相对较小，仅采用提升模量减缓裂缝扩散的方案是不合理的。

3.4.5旧水泥混凝土板接缝宽度变化对KI(t,θ)的影响

保持车速为80 km/h不变，采取0.2 cm逐级递增，接缝宽从0.2 cm增长至2 cm。计算结果见图17。

(a)1 cm裂缝长度

结合图17得知动应力强度因子数值伴随接缝宽增加而不断增大，特别是裂缝扩展后期所产生的影响相对显著。1、4与8 cm裂缝的最高KI值从接缝宽度0.2 cm提升至2 cm的情况时增加幅度分别为19.3%、24.1%和33.1%。结合研究可知接缝宽对强度因子的影响较小，核心原因是接缝自身不具备传荷能力，接缝增长对水泥板总面积影响偏小。

4 结语

本文以广西南宁市现有高速公路东环改造二期工程为例，基于动力学理论等开展分析，探讨动荷载作用下沥青加铺层反射裂缝的强度因子变化规律，涉及分析参数有车速、轴载、结构层厚度和模量等。通过计算分析得到如下结论：

a.动应力强度因子伴随速度提升数值逐渐减小，意味着车速越快，对裂缝增长所构成的影响相对较小。

b.伴随车辆轴载的提升动应力强度因子逐渐增大，表明轴载会有显著加快裂缝扩展，为了应对该问题应当严格限制超重车辆的行驶，减缓裂缝的发育。

c.伴随反射裂缝长度的增长，对应的动应力强度因子曲线逐步向上突起，随着裂缝长度的增幅越来越大，意味着伴随裂缝的不断扩展，扩展相同裂缝长度可承受的荷载次数不断减小。

d.伴随加铺层厚度或模量增大，动应力强度因子时程曲线逐渐减缓。增加加铺层的厚度可降低强度因子数值，如果仅是采用提升厚度的方式来延缓裂缝的扩展并不科学。提升加铺层模量有助于减弱动荷载所构成的影响，其具体的选择应当系统考虑多方面的影响要素。

e.伴随应力吸收层厚度的增加或者弹性模量的增大，动应力强度因子时程曲线逐渐减缓。适度的应力吸收层厚度有必要，但是过厚吸收层无法实现很好的减弱效果又浪费资源。模量所产生的实际影响相对偏小，单纯通过模量的提高来减弱裂缝的扩展是不经济的。

f.旧水泥板接缝宽度对于裂缝的扩展影响相对偏小，主要原因为接缝自身并不具备传递荷载的能力，接缝宽度在混凝土板面积中所占的比例很小。