一种产生双频涡旋电磁波的反射型超表面

王俊磊, 韩国瑞, 袁 浩, 陈新伟

(山西大学 物理电子工程学院, 山西 太原 030006)

0 引 言

随着现代社会技术的发展和无线通信用户数量的不断增加, 有限的带宽范围限制了无线通信技术的发展。 OAM由于模式之间相互正交以及模式的无限性[1], 对于扩大信道容量具有重要的意义, 因而引起了研究者的广泛关注。 20世纪90年代, G.A.Turnbull等[2]利用螺旋相位板, 首次产生了毫米波频段的涡旋电磁波; 2007年, B. Thidé等[3]提出用圆形阵列天线调相的方法, 在低频段生成了的涡旋波。 当前, 在太赫兹波段利用超表面生成涡旋波束也有丰硕的成果[4-6]。 在微波波段, Q.Bai等[7]提出了一种矩形微带贴片阵元和微带移相馈电网络组成的相控阵天线, 通过计算中心馈电点到微带贴片之间的微带线长度, 使得相邻微带贴片之间的相位相差45°, 并首次在10 GHz下通过实验证明可以产生l=±1的涡旋电磁波, 然而, 馈电网络的设计过于复杂; Liu B.Y.等[8]提出了一种基于折叠反射阵列的具有可编程特性的OAM发生器, 可以在9.5 GHz～10.5 GHz频率范围内产生高增益的OAM模式可重构波束, 但需要独立控制各单元的相位状态, 电路结构繁琐且制作成本较高; Chen G.T.等[9]设计了一种由在两个介质基板上蚀刻的两个菱形金属贴片组成的双线性极化单元, 由此单元所设计的超表面阵列由于其双层结构, 导致加工难度较大; Z.Akram等[10]提出了一种1/4波长的单元, 单元由方形环、 交叉偶极子和4个方形贴片组成, 可以在6 GHz频率下实现360° 的相位覆盖范围, 设计并制造了一款宽带涡旋波反射阵列, 在6 GHz频率下能够生成l=+2模式的OAM涡旋波; Huang H.等[11]设计了一款由 10×10 个单元构成的小型化高效平面反射型超表面, 单元是由两个同心圆环组成的, 通过调节圆环的半径, 可以生成不同模式的OAM 涡旋波束, 测试结果表明, 该天线阵列在中心频率5.8 GHz 处生成了l=+1的 OAM 涡旋电磁波。 但上述两种超表面反射阵列仅工作在单一频率, 不能充分利用频谱资源; 孙胜等[12]提出了一种基于反射超表面的偏馈式涡旋波产生装置, 实现了场增强低交叉极化涡旋波的产生。 为了改善螺旋相位板尺寸过大、 贴片阵列天线馈电网络复杂、 工作频率单一的问题, 可以设计双频的反射型超表面。

本文设计了一种加载传输线型的双对称C型环超表面单元, 由此单元构成了一款工作于双频波段的超表面。 通过改变加载传输线的长度, 可以在两个频率处达到360°的相位覆盖范围, 同时, 不同频率之间可以实现独立调控。 基于此单元, 设计了工作在8 GHz和18 GHz 的13×13单元的双频反射型超表面。 仿真结果表明, 所设计的超表面在两频率处均生成了l=+1 模式的OAM 涡旋波束, 同时具有结构简单、 尺寸小等优点。

1 设计原理

本文所设计的超表面阵列结构如图1 所示, 由馈源喇叭和超表面反射阵列组成。 根据广义斯涅尔定律[13], 若要生成OAM涡旋波束, 则需要在超表面上引入相位因子exp(jlφ), 即需要对超表面上每个单元进行相位补偿。 馈源喇叭辐射出的球面波经过不同的路径照射到反射阵列上的单元, 从而产生了不同的相位差。 通过计算各位置所需的相位补偿, 进而改变超表面各单元的加载传输线的长度, 即将不同尺寸的单元与每个位置所需相位补偿一一对应, 从而生成OAM涡旋波束。

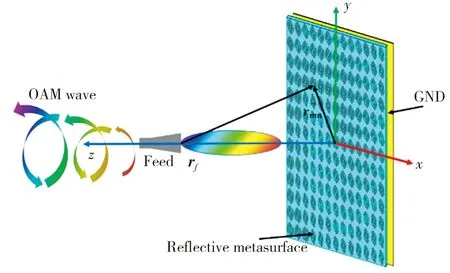
图1 OAM涡旋波束生成示意图Fig.1 Schematic diagram of OAM vortex beam generation

根据阵列天线理论[14], 反射单元需要对馈源喇叭天线的相位延迟进行补偿, 才能形成平面波, 所需相位补偿为

Δφr(x,y)=k0(|rf-rmn|-rmn·u),

(1)

式中:k0为自由空间中的波数;rf为喇叭天线相位中心矢量;rmn为第(m,n)单元的位置矢量(xm,yn, 0);u为OAM涡旋波束的方向。

同时, 基于反射阵天线的OAM涡旋电磁波束的设计, 是在生成平面波的基础上引入一个螺旋相位因子。 即在式(1)中加上螺旋相位的变化, 如

(2)

式中:l为OAM涡旋波的模式数。

因此, 超表面反射阵列生成OAM 涡旋波束所需的总相位为

φr(x,y)=k0(|rf-rmn|-rmn·u)+

(3)

通过式(3), 可以计算出生成任意模式数的OAM 涡旋波束的相位, 再通过所需相位与单元之间的转换, 即可排列出符合要求的反射型超表面。

2 结构设计

基于以上工作原理, 设计了一款加载相位延迟的线型反射单元, 其结构如图2 所示。 该结构由关于中心对称的内部C型环和外部C型环构成, 在内部C型环和外部C型环上加载长度可调节的相位延迟线, 延迟线逆时针延伸。 通过改变延迟线长度, 来控制反射相位; 延迟线和C型环分别由宽度为0.25 mm和0.5 mm的金属贴片连接。

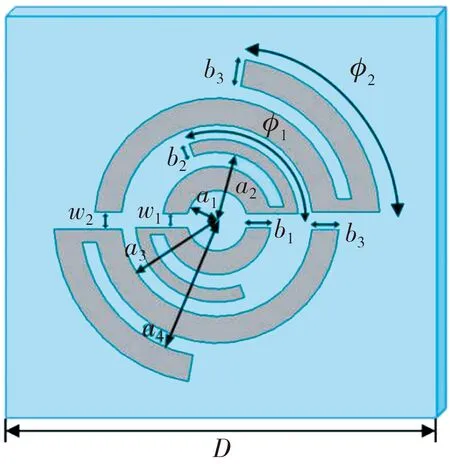
(a) 顶视图

该结构单元印刷在厚度为1 mm、 边长为14 mm的正方形F4B(εr=2.2)介质基板上, 在介质基板下方2 mm处设置与介质基板同大小的接地板, 介质基板和接地板之间是2 mm的空气层。 详细结构参数如表1 所示。

表1 超表面单元结构参数Tab.1 Unit cell structure parameters of metasurface

通过使用仿真软件CST Microwave Studio对超表面单元中C型环工作在8 GHz和18 GHz进行了分析。 在保证内部结构不变, 而改变外部C型环的延迟线的长度, 即φ2的大小发生改变情况下, 对应的幅度和相位变化曲线如图3 所示, 从图3 可以看出, 在8 GHz时, 当内部C型延迟线φ1分别取15°, 35°, 75°, 115°, 随着φ2由5°变化到175°, 外部延迟线的长度逐渐增加, 反射波的相位改变量超过400°, 幅值达到0.9以上, 说明通过改变外部相位延迟线对应的圆心角φ2可以独立调控相位, 与内部延迟线没关系。

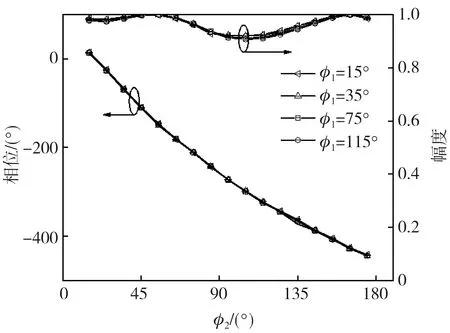
图3 在8 GHz时单元的幅值和相移曲线Fig.3 Magnitude and phase shift curves of the unit cell at 8 GHz

在保证外部结构不变, 而改变内部C型环延迟线的长度, 即φ1的大小发生改变情况下, 对应的幅度和相位变化曲线如图4 所示。 从图4 可以看出, 在18 GHz时, 当外部C型延迟线φ2分别取70°, 90°, 110°, 130°, 随着φ1由5°变化到175°, 内部延迟线的长度逐渐增加, 反射波的相位改变量超过400°, 幅值达到0.9以上, 说明通过改变内部相位延迟线对应的圆心角φ1, 可以独立调控相位, 与外部延迟线没关系。

图4 在18 GHz时单元的幅值和相移曲线Fig.4 Magnitude and phase shift curves of the unit cell at 18 GHz

由上述分析可知, 在工作频率为8 GHz时, 通过改变变量φ2, 可以调节低频时的相位, 此时φ1可以任意取值; 在工作频率为18 GHz时, 通过改变变量φ1, 可以调节高频时的相位, 此时φ2可以任意取值; 两频率之间能够实现独立的相位控制且互不影响, 且反射幅值均超过0.9, 反射相位覆盖范围均超过360°。

3 超表面设计

将上面设计的超表面单元周期排列成13×13的阵列, 构成反射型低剖面双频超表面OAM反射阵列天线, 超表面的大小为182 mm×182 mm。 通过设计原理中的相位补偿公式, 计算出生成不同模式OAM涡旋电磁波的单元内、 外相位延迟线相位需求, 再根据相移曲线调节内、 外相位延迟线的尺寸, 最后, 设计出所需的超表面反射阵列。 本节在8 GHz 生成l=+1 , 在18 GHz 生成l=+1模式的OAM 涡旋电磁波, 仿真分析了一款超表面。

具体设计过程如下: 首先, 计算出在8 GHz处生成l=+1模式的涡旋波所需的相位补偿量, 如图5(a)所示, 再通过图3 所示的相移曲线将相位补偿量转换为加载相位延迟线的长度所对应的圆心角的大小, 得到图6(a)所示; 采用同样的方法, 可以得到在18 GHz处生成l=+1模式涡旋波的单元大小。 将内部结构与外部结构按图6 排列组合后最终形成反射型双频超表面, 如图7 所示。

(a) 8 GHz处所需的相位补偿量

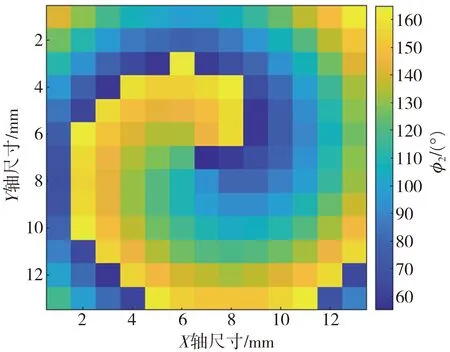
(a) 外部结构尺寸大小

图7 双频超表面反射阵列

4 结果分析

对上节所设计的超表面反射阵列天线进行了仿真。 使用喇叭天线在8 GHz距离超表面反射阵列150 mm , 18 GHz距离超表面反射阵列300 mm处进行馈电, 图8 为在8 GHz 工作频率处的三维方向图和电场相位图。 图9 为在18 GHz 工作频率处的三维方向图和电场相位图。 通过观察电场相位图可知, 在8 GHz 和18 GHz 处均生成了l=+1的OAM 涡旋波束。 从三维方向图可以看出, 在8 GHz 和18 GHz 处所生成的OAM 涡旋波束均有较为明显的中空特征, 即产生了由相位奇点引起的零强度中心。 图10 为超表面天线阵列的Phi=0°和Phi=90°辐射方向图, 8 GHz 时l=+1 模和18 GHz 时l=+1模的最大增益分别为 16.2 dBi 和 21.6 dBi。 因此, 本文所设计的反射型超表面可以在两个频段内同时生成OAM涡旋电磁波。

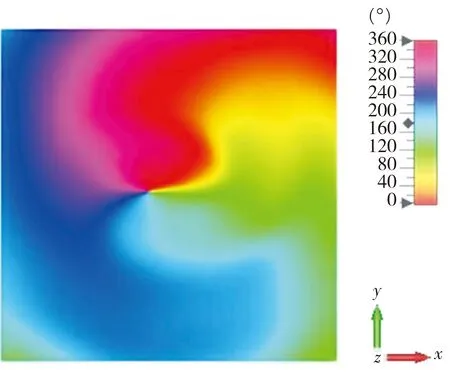
(a) 电场相位分布图

(a) 电场相位分布图

(a) 8 GHz辐射方向图

表2 给出了本文与参考文献的性能比较。 从表中的数据可以看出, 本文所设计的超表面是单层结构, 且工作在两个频段, 同时具有较高的增益。

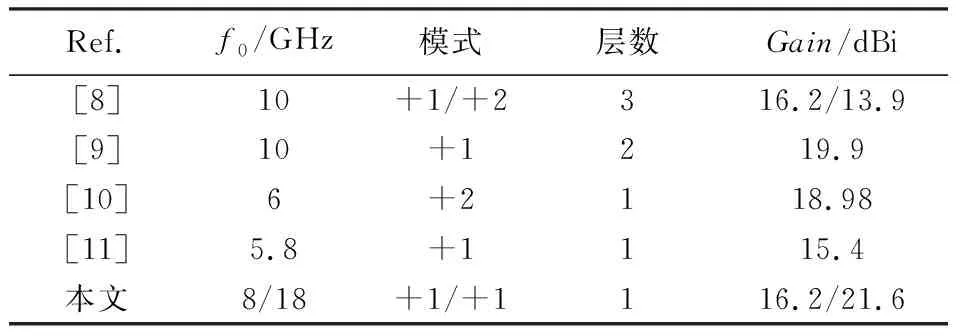
表2 文献对比Tab.2 Comparison of references

根据上述分析结果, 加工制作了所设计的双频涡旋波超表面, 如图11 所示, 并对超表面Phi=0°和Phi=90°的二维辐射方向图进行测量。 由于超表面阵列加工的精度以及测试条件的局限性, 导致测量与仿真结果存在一定误差。 图12 为8 GHz和18 GHz时归一化的Phi=0°和Phi=90°辐射方向图仿真与测量结果对比, 从图中可以看出, 测量的辐射方向图主波束方向都具有明显的中心凹陷, 符合涡旋电磁波“甜甜圈”形的电场特征。 综合仿真与测量结果, 误差在允许范围之内, 符合预期设计要求。

图11 超表面原型Fig.11 Prototype of the metasurface

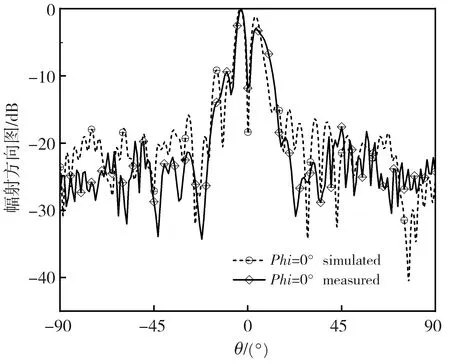
(a) 8 GHz时Phi=0°对比

5 结 语

本文设计了一款在两个频段内均能生成OAM涡旋电磁波的反射型超表面。 该超表面由加载相位延迟线的双对称C型环单元构成, 通过改变内外对称C型环相位延迟线的长度, 可以在两个频段范围内达到360°的相位覆盖范围, 仿真与测试结果表明, 所设计的反射型超表面在两个频段内均能生成l=+1模式的OAM涡旋电磁波, 在8 GHz增益达到了16.2 dBi, 在18 GHz增益达到了21.6 dBi。 设计的双频反射型超表面结构简单, 剖面较低, 在轨道角动量复用技术中具有良好的实用性。