基于点源成像的微球成像分辨能力仿真分析
王宇莹, 洪羽剑, 卢钧胜,2, 曾婧潇, 付晓锋, 胡晓东
(1. 天津大学 精密仪器与光电子工程学院, 天津 300072; 2. 天津工业大学 生命科学学院, 天津 300387)
光学显微镜丰富了人们对于微观世界的认识, 在生物医学、 材料科学等领域都有着广泛的应用[1-2]。 然而, 传统光学显微镜的分辨能力会受到衍射极限的限制[3]。 为了提高成像分辨能力, 2011年, Zengbo Wang等[4]提出了基于微球透镜的显微成像技术, 使用直径为2 μm~9 μm的二氧化硅微球, 结合80×, NA=0.9的物镜, 成功在卤素灯照明下实现了最小尺寸为50 nm的微结构的观测。 2022年, Yurong Cao等[5]使用完全浸没于PDMS、 直径为30 μm的钛酸钡微球辅助显微镜, 对金、 银、 铬制成的纳米颗粒样品进行了成像, 能够分辨出130 nm的间隙距离。 Jianguo Wang等[6]优化了浸没介质, 直径为10 μm的PS微球在半浸没状态下可以清晰分辨出直径为200 nm的二氧化硅纳米粒子阵列。 基于微球透镜的显微成像技术具有成像系统简单、 可实时成像、 不需要荧光染料进行标记等优点, 具有重要的研究意义和广阔的应用前景。
2015年, T.X.Hoang等[7]基于米氏理论, 仿真了微球对点光源的成像过程, 指出在共振模式下其分辨能力有显著提升; 2016年, A. V. Maslov和V. N. Astratov[8]对微球成像系统进行了二维仿真, 分析了光源相干性对微球分辨能力的影响, 发现相干光源照明条件下具有更高的分辨能力; 2020年, L.Y.Yu等[9]建立了三级全波模拟体系来深入分析微球的成像特性, 研究了样品的材料属性对微球分辨率的影响, 结果表明, 金属样品具有更好的成像效果。 以上研究工作分析了共振模式、 照明条件、 样品材料等对成像分辨能力的影响, 然而缺乏对于微球尺寸等成像系统参数变化如何影响成像分辨能力的仿真分析。 目前, 还有许多研究者已经开展了使用悬臂梁控制抬高微球脱离样品表面的成像实验[10-12], 然而在实验中并没有分析微球和样品距离的变化对成像放大倍数和成像分辨能力产生的影响。
因此, 本文提出了一种基于点源成像的仿真计算方法, 通过仿真, 分析了成像系统参数的变化对成像分辨能力产生的影响, 从而能够更好地指导实验。 首先, 使用COMSOL软件仿真了微球与点光源相互作用的过程; 再基于角谱法将仿真得到的远场进行反向传播, 获得了微球对点光源的成像结果, 从而对分辨能力进行分析。 本文分别设计了点光源与微球下端间距为5 nm以及点光源与微球下端间距为100 nm~1 000 nm的仿真模型来模拟实验中微球紧贴样品以及抬高微球脱离样品表面两种情况。 在微球紧贴点光源的模型中, 仅改变微球半径, 仿真分析了微球半径变化对成像分辨能力的影响; 然后, 在仿真模型中移动点光源位置, 分析了微球和点光源距离变化对成像分辨能力的影响。
1 基本原理与方法
本文使用COMSOL软件仿真了微球与点光源的相互作用过程, 仿真模型如图1 所示。 微球半径为R, 折射率为nm, 环境介质的折射率为nb, 点光源位于微球正下方, 与微球下端之间的距离为d, 波长为600 nm。 远场观察线相对于点光源的数值孔径为0.9, 模拟显微镜物镜对光场的收集, 记录下远场观察线上的场分布, 再利用角谱理论对平面波反向传输计算, 重构出点源的像。
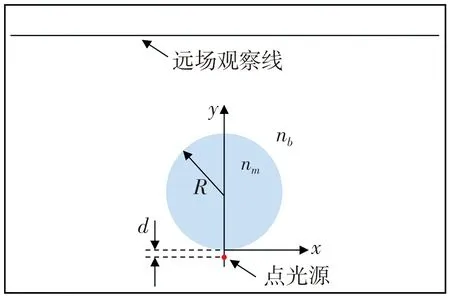
图1 仿真模型Fig.1 Simulation structure
根据角谱理论, 记录平面和待测平面的光场都可以看成是由无数组传播方向不同、 幅值不同的平面波叠加而成, 在叠加时每个单色平面波分量的振幅和相位都由相应平面上光场的角谱Ai(fx,fy)和A(fx,fy)决定, 其中fx=cosα/λ,fy=cosβ/λ, cosα和cosβ为传播方向的方向余弦,λ为波长。 记录平面和待测平面的光场可以分别表示为
Ui(xi,yi)=
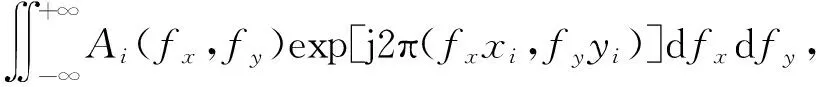
(1)
以及
U(x,y)=

(2)
由式(1)和(2)可知, 根据Ai(fx,fy)和A(fx,fy)之间的关系, 可以计算得到在传播过程中每一个平面波分量的振幅和相位的变化, 从而得到整个光场从记录平面到待测平面所发生的变化。 角谱传播规律的基础是标量波动方程
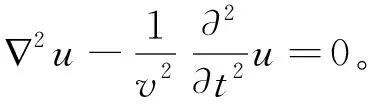
(3)
所以, 根据标量衍射的亥姆霍兹方程, 可以得到Ai(fx,fy)和A(fx,fy)之间的关系式
Ai(fx,fy)=

(4)
其中, 传递函数H(fx,fy)的表达式为
H(fx,fy)=
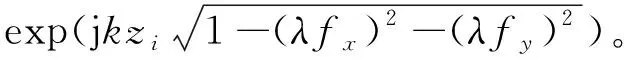
(5)
式(4)描述了角谱的传递规律, 根据记录平面上的角谱, 就可以得到待测平面上的角谱, 然后进行傅里叶逆变换, 就可以得到待测平面光场的复振幅分布, 计算公式为
Ui(xi,yi)=F-1{F[U(x,y)]×H(fx,fy)}。
(6)
因此, 基于角谱法, 可以将远场观察线位置处的场反向传播到空间中的任何平面位置, 此处选择重构图像沿y轴强度最强位置为微球对点光源的成像位置y′。 为了分析微球尺寸以及微球和样品距离对成像分辨能力的影响, 采用如图2 所示的方式, 根据成像位置和点光源的位置, 可计算得出成像放大倍数

图2 点源成像放大倍数计算示意图Fig.2 Schematic diagram of point source imaging magnification calculation
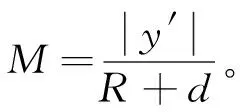
(7)
点源成像的图样宽度用点扩散函数(point spread function, PSF)的半高全宽值(full width at half maximum, FWHM)来表示, 即w。 通过计算点源成像图样宽度和放大倍数的比值来分析微球的成像分辨能力[13], 即w/M, 该比值越小说明分辨能力越强。
2 仿真结果与分析
2.1 微球尺寸对分辨能力的影响
为了分析微球尺寸对成像分辨能力的影响, 仿真了不同尺寸微球对距微球下端距离d均为5 nm的点光源的成像过程。 在仿真模型中设定微球折射率nm为1.46, 环境介质的折射率nb为1, 波长λ为600 nm。 以0.5 μm为间隔改变微球的半径值R, 从5 μm增大至10 μm。 微球半径分别为6.5 μm和8.5 μm时的仿真结果如图3(a)和图3(c)所示, 在相对于点光源的数值孔径为0.9的位置划定远场观察线, 模拟显微镜物镜对光场的收集, 并基于角谱法将仿真结果中远场观察线处的场分布进行反向传播, 计算得到其成像结果分别如图3(b)和图3(d)所示。
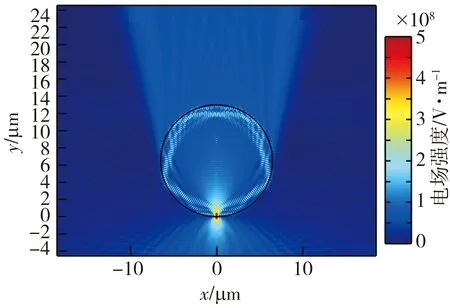
(a) 点光源位于半径为6.5 μm的微球下方5 nm处的仿真结果
计算并绘制得到成像图样宽度和放大倍数的比值w/M随微球半径R的变化曲线, 如图4 所示。 微球半径为5 μm时,w/M最小, 约为0.37λ。 当R从5 μm增大至10 μm时,w/M从0.37λ增大至0.52λ, 可以看出分辨能力随微球尺寸的增大而降低, 增长趋势逐渐趋于平缓。 仿真结果表明, 在其他参数保持不变时, 减小微球的半径可以有效地提高分辨能力。

图4 成像图样宽度和放大倍数的比值与微球半径的关系Fig.4 Relationship between w/M and radius of microsphere
由图4 可知, 成像图样宽度和放大倍数的比值与微球半径的关系曲线在R=9 μm处下降,R=9 μm时的仿真结果如图5 所示, 此时出现了明显的共振现象, 因此其分辨能力得到了提高。
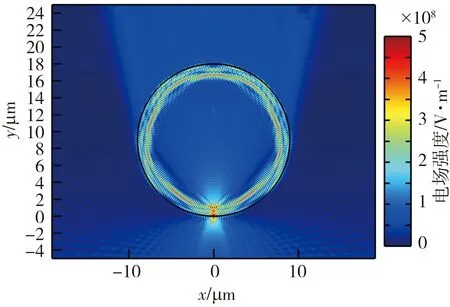
图5 点光源位于半径为9 μm的微球下方5 nm处的仿真结果Fig.5 The field intensity for a point source located at d=5 nm below the microsphere of R=9 μm
2.2 点光源与微球的距离对分辨能力的影响
为了分析点光源与微球的距离的变化对分辨能力的影响, 在仿真中改变了点光源和微球之间的距离, 模拟了微球对不同位置样品的成像。 在仿真中, 选取了半径分别为5 μm, 7.5 μm和10 μm的微球(微球折射率nm为1.46)进行分析, 环境介质折射率nb为1, 波长为600 nm, 仍与2.1节保持一致。 将点光源和微球下端的间距d从5 nm增加至1 000 nm, 仿真并计算得出微球对不同位置点光源进行成像的结果。 微球半径为7.5 μm时, 点光源和微球下端的距离d分别为200 nm和600 nm时的仿真结果如图6(a)和图6(c)所示, 在相对于点光源的数值孔径为0.9的位置划定远场观察线, 模拟显微镜物镜对光场的收集, 并基于角谱法将仿真结果中远场观察线处的场分布进行反向传播, 计算得到其成像结果, 分别如图6(b)和图6(d)所示, 二者对比可以看出, 点光源和微球距离增大时, 其成像图样宽度变宽。

(a) 点光源位于R=7.5 μm的微球下方d=200 nm处的仿真结果
计算和分析不同直径微球对不同位置点光源的成像分辨能力, 表1~表3 展示了半径分别为5 μm, 7.5 μm和10 μm的微球对不同位置点光源的成像图样半高全宽w、 放大倍数M以及二者的比值w/M。
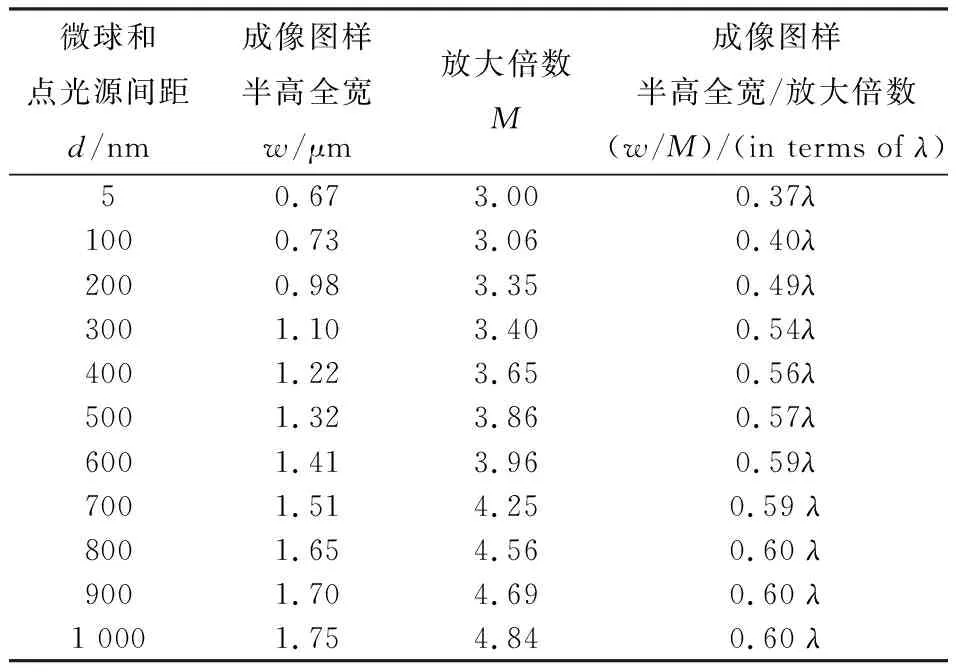
表1 半径为5 μm的微球对不同位置点光源的成像图样宽度、 放大倍数及二者比值Tab.1 Simulatedw, magnification M, and ratio w/M of 5 μm-radius microsphere based imaging system for different positions of the point source
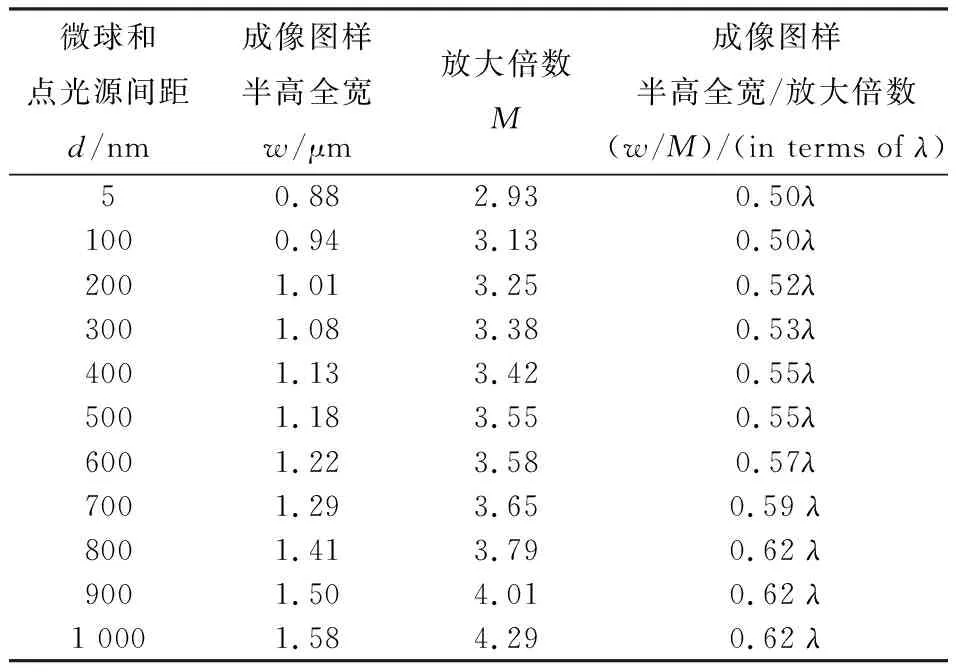
表2 半径为7.5 μm的微球对不同位置点光源的成像图样宽度、 放大倍数及二者比值Tab.2 Simulatedw, magnification M, and ratio w/M of 7.5 μm-radius microsphere based imaging system for different positions of the point source
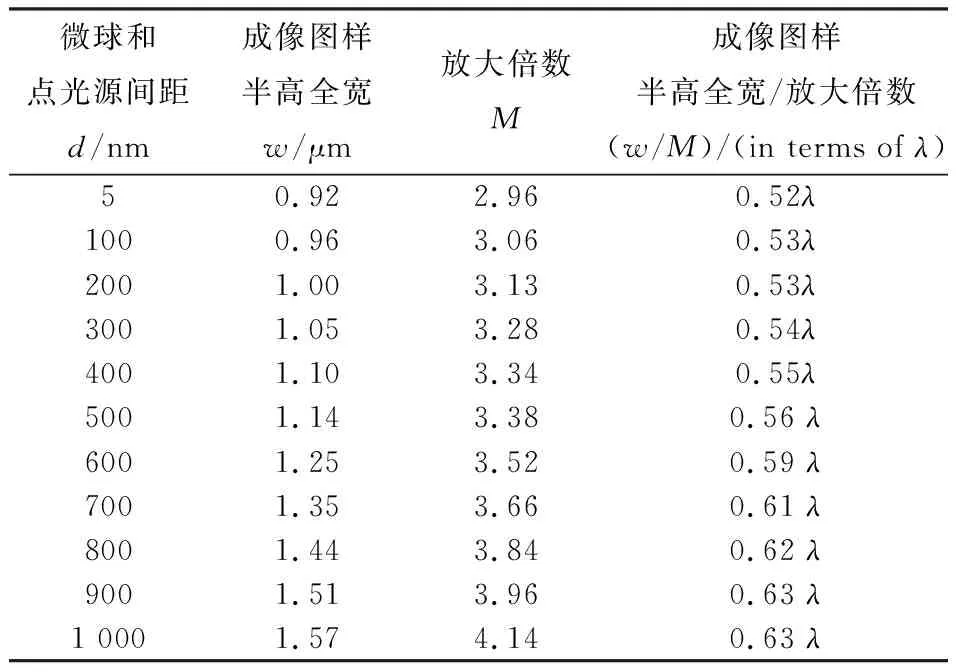
表3 半径为10 μm的微球对不同位置点光源的成像图样宽度、 放大倍数及二者比值Tab.3 Simulatedw, magnification M, and ratio w/M of 10 μm-radius microsphere based imaging system for different positions of the point source
表1~表3 的结果表明, 随着点光源和微球之间距离d的增加, 成像图样宽度w随之增大, 在图6中也有较为直观的体现, 放大倍数M随d的增大而增大。 以半径为5 μm的微球为例, 随着点光源与微球之间的距离d从5 nm增加至1 000 nm,w从0.67 μm增加至1.75 μm, 同时, 其成像放大倍数M从3增加至4.84, 这与几何光学的透镜成像规律具有相似性。 随着d的增加, 半径为7.5 μm和10 μm微球的w和M也具有同样的变化趋势。 对w/M进行计算, 可以对分辨能力的变化趋势进行分析, 当点光源和微球的距离从5 nm增加至1 000 nm时, 半径为5 μm微球的w/M从0.37λ增大至0.60λ, 半径为7.5 μm微球的w/M从0.5λ增大至0.62λ, 半径为10 μm微球的w/M从0.52λ增大至0.63λ。 通过w/M的变化趋势对分辨能力进行分析可知, 当间距小于800 nm时, 分辨能力随着点光源和微球距离的增加有明显的下降趋势。 当间距增大至800 nm~1 000 nm时, 其成像倍数仍然在增大, 但是分辨能力并没有明显的下降, 这一结果与Martí Duocastella[14]提出的“空放大效应”一致。
分析微球分辨能力随间距d的增大而下降的原因, 本文认为, 根据Abbe的成像理论, 物平面的光场分布是由不同空间频率信息线性组合而成的, 可以将在空间中传播的波表示为
E=Aexp(ikr)=
Aexp[i(xkx+yky+zkz)]=
Aexp[i(xkx+yky)]*exp(izkz),
(8)
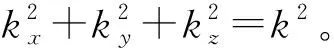
微球成像过程中倏逝波被耦合进微球并转换成微球内的传输波, 从而散射至远场参与成像[15]。 而随着微球和点光源距离的增加, 倏逝波不断衰减, 微球可以收集到的高频信息也随之减少, 因此, 成像分辨能力也随之降低。 当距离增大至800 nm时, 倏逝波衰减趋于0而无法被耦合进微球, 因此, 此时距离继续增大, 其分辨能力没有明显变化。
3 结 论
本文设计了微球对点光源成像的仿真模型, 并对微球的成像分辨能力进行了分析。 结果表明, 微球尺寸的增加以及微球和点光源距离的增加, 都会使分辨能力下降, 并根据微球通过耦合近场倏逝波提高成像分辨能力的理论对结果进行了合理的解释。 仿真结果对基于微球透镜的成像实验具有指导意义: 为了提高成像分辨能力, 在实验条件允许的情况下, 可以选择小尺寸微球; 当需要抬高并控制微球位置从而对样品不同区域进行成像时, 仿真结果表明, 成像分辨能力将随着微球和样品距离的增加而下降, 因此, 在实验中应当小幅度准确地调控距离, 使样品与微球间距离小于800 nm, 以获得更好的成像效果和更高的分辨能力。 本文提出的微球成像仿真分析方法也对今后开展微球成像分辨能力的相关仿真分析工作提供了方法基础。

