基于残差图卷积网络的运动想象任务分类

汪 健, 乔晓艳

(山西大学 物理电子工程学院, 山西 太原 030006)

0 引 言

脑-机接口(Brain-Computer Interface, BCI)是一种实现人类大脑与外部设备连接通路的人机交互技术, 在医疗康复、 军事、 娱乐、 人工智能等领域应用前景广阔[1]。

脑电信号解码是BCI技术的关键环节。 对运动想象任务的脑电解码, 传统机器学习方法采用傅里叶变换、 小波变换、 共空间模式等对运动想象脑电信号(motor imagery electroencephalogram, MI-EEG)进行特征提取, 再用支持向量机、 K 近邻等算法进行运动想象任务分类。 Sharma等[2]在BCI Competition IV Dataset1数据集上使用RBF 内核的支持向量机分类器和K近邻分类器, 分别获得80%和72.5%的分类准确率。 近年来, 深度学习方法被用于MI-EEG分类, 可直接从EEG中学习特征并实现分类, 应用最多的是卷积神经网络(convolutional neural network, CNN); Amin等[3]提出一种从EEG数据中捕获时空特征的MCNN方法, 在 BCI Competition IV 2a数据集上实现了 75.7%的任务分类准确率; Zhang等[4]提出了一种基于迁移学习的混合深度神经网络(HDNN-TL)处理BCI Competition IV2a数据集4类MI任务, 取得了0.81的平均kappa系数。

图结构包含节点信息和连接边信息, 图卷积神经网络(Graph Convolutional neural Network, GCN)是在非欧氏空间结构数据上的深度学习, 既能学习节点特征, 又能获得节点之间的关联信息。 受图数据结构启发以及多导联脑电具有的空间分布特性, 采用图卷积网络对MI-EEG数据进行解码, 可以从大脑空间关联中提取更多有价值的特征信息, 提高BCI运动想象任务分类的准确率。 由于图卷积存在网络退化问题, 目前多采用浅层图卷积网络实现运动想象任务分类[5]。 李珍琦等[6]提出了一种融合注意力的多维特征图卷积网络(AMFGCN), 能提取脑电信号在时频空域上的信息, 再融合注意力机制捕获各维度的动态关联强度, 在BCI Competition IV2a数据集上取得 85.74%准确率和 0.809 8的 kappa 系数; Sun B等[7]提出一种自适应时空图卷积网络(ASTGCN), 利用脑电信号时域特性和空域的通道相关性, 取得了90.6%平均分类准确率。 由于浅层图卷积网络对脑电信号特征提取能力有限, 深层网络的性能要比浅层网络好。 然而, 随着网络层数加深, 图模型性能难以提高, 这种现象为网络退化。 残差网络可有效改善模型因深度增加而产生的梯度消失、 梯度爆炸以及网络退化等问题[8]。 在深层图卷积网络中嵌入残差学习, 能提取到脑电更多的深层特征信息, 并且能使模型收敛和防止网络退化。 因此, 设计深层残差图卷积网络, 进行运动想象任务分类。 首先, 根据脑电电极的天然空间分布和相互关联性, 构建脑电图网络; 其次, 将图卷积网络和残差学习结合, 并利用分层图池化方法, 每两个图卷积构成一个残差块, 经过激活函数后添加一个图池化层, 实现深层残差图卷积网络模型对4类运动想象任务分类; 最后, 在不同BCI数据集上对提出的运动想象任务分类模型性能进行客观评价和分析, 验证模型的可行性、 有效性以及泛化能力。

1 算法基本原理

1.1 谱域图卷积

图卷积的本质是找到适用于图的可学习卷积核。 基于谱域的图卷积是根据图谱理论和卷积定理在谱域上定义卷积, 通过傅里叶变换, 将节点映射到频域空间, 在此空间做乘积来实现时域卷积[9]。 谱域图卷积是基于全图的傅里叶变换来实现图的卷积, 该方法无法保证局部性。 由于谱域图卷积方法的时空复杂度太高, 采用切比雪夫网络(ChebyNet)[10]对卷积核gθ进行参数化, 用切比雪夫多项式代替谱卷积的卷积核, 其逼近的卷积核为

(1)

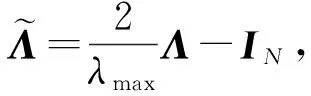
Tn(x)=2xTn-1(x)-Tn-2(x)。

(2)

对于输入x, ChebyNet 图卷积运算为

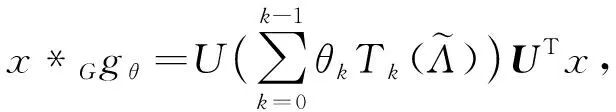
(3)

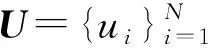
(4)

ChebyNet利用切比雪夫多项式代替谱域卷积核, 实现谱域图卷积, 免去了对拉普拉斯矩阵进行特征分解的复杂过程; 卷积核只有K+1个可学习的参数;K为“感受野”半径, 卷积核具有严格的空间局部性。

1.2 分层图池化

分层图池化方法是对图卷积分层进行图池化, 提取图的节点特征和局部结构信息并生成图表示。 EigenPooling图池化[11]是基于子图的特征向量设计的一种池化。 其主要由两步完成: ① 图粗化(graph coarsening), 根据谱聚类算法将原始图G划分为一组子图, 并将子图视为超节点形成粗化图(coarsened graph)。 粗化后的邻接矩阵为Acoar=STAS, 表示超节点之间的连接强度。 ② 将在原始图上定义的图信号池化为该图的粗化图上定义的图信号。 在确定粗化图及相应的邻接矩阵后, 对每个粗化图内的信息整合抽取, 使得以分层的方式逐层学习图表示成为可能。 子图与超节点之间是一一对应的, 保证了网络连接的稀疏性, 且大大降低了参数量和计算开销。 将EigenPooling与GCN相结合, 在6个常用的图像分类基准数据集上进行仿真实验, 均获得较好的结果, 证明了其有效性[11]。

1.3 残差学习

当输入为x, 学习到的特征为H(x)时,H(x)即为想要得到的映射。 将x直接连接到输出, 在输入和输出之间做恒等映射(identity)。 定义F(x)=H(x)-x为残差, 让非线性层Relu拟合F(x), 则原始映射为F(x)+x。 若F(x)为0, 下一层的输入为x, 即为一个恒等映射。 残差块结构如图1 所示。

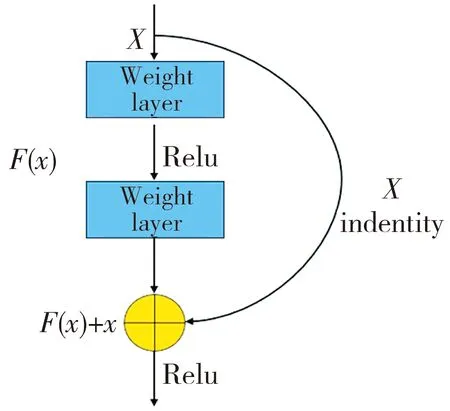
图1 残差学习: 一个残差块Fig.1 Residual learning: a residual block

利用图卷积神经网络处理非欧几里得数据的应用中, 构建图数据的高级特征需要在深层模型下才能提取得到。 大量研究表明, GCN 不能很好地扩展到深度模型架构[9,12], 因为堆叠多层图卷积会出现网络退化, 加大反向传播的复杂性。 受残差连接的启发, 将图卷积网络和残差学习相结合, 在几个图卷积层之间添加残差连接构成一个残差块, 再由多个残差块组合构成残差图卷积网络。 这样既可以学习到图数据的高级特征信息, 又能避免网络出现退化问题。

2 实验数据来源与预处理

2.1 实验数据集

本文使用的第一个数据集是BCI Competition IV 2a (http://www.bbci.de/competition/iv/。 该数据集包含9名被试进行左手、 右手、 双脚和舌头4类运动想象任务, 使用22个Ag/AgCl电极以250 Hz采样率采集脑电数据, 每名被试在不同日期记录了两组运动想象脑电数据。 每组试验中每名被试进行6轮运动想象, 每轮包括4种运动想象任务各12次, 共得到288次试验样本。 实验范式如图2 所示。

图2 BCI IV 2a运动想象实验范式Fig.2 BCI IV 2aexperimental paradigm of motor imagery

另一个数据集是BCI Competition III IIIa (http://www.bbci.de/competition/iii/)。 该数据集包含3名被试进行左手、 右手、 双脚和舌头4类运动想象。 使用Neuroscan 的 64 通道 EEG 放大器采集脑电信号, 采样频率250 Hz, 试验记录60个电极EEG数据。 被试K3b共360次试验样本, 被试K6b和L1b各有240次试验样本。 实验范式如图3 所示。

图3 BCI III IIIa运动想象实验范式Fig.3 BCI III IIIa experimental paradigm of motorimagery

2.2 数据预处理和数据增强

ERD/ERS现象主要发生在EEG的μ节律(8 Hz～12 Hz)和β节律(13 Hz～30 Hz), 能被用来作为脑机接口运动想象任务分类的依据, 有效获知被试的运动意图。 本文对原始EEG进行8 Hz～30 Hz带通滤波, 并做独立成分分析, 以去除眼电、 肌电等伪迹, 获得纯净的脑电信号。 对BCI IV 2a数据集按实验范式提取3 s～6 s的脑电信号, 对BCI III IIIa数据集按实验范式提取3 s～7 s的脑电信号, 并与想象任务标签对应。 本文对BCI IV 2a和BCI III IIIa数据集预处理和数据增强方法相同, 以下仅以BCI IV 2a数据集为例说明。

运动想象脑电数据采集成本高, 数据样本量较少, 可采用滑动窗方法扩增脑电数据[13]。 分别以2 s和1 s为滑动窗时长, 间隔0.5 s和0.25 s滑动。 先将BCI IV 2a数据集每名被试2个日期的脑电数据合并, 则每名被试有576个原始样本, 之后再进行滑动。 对每名被试的脑电数据样本按8∶2划分训练集和测试集, 经扩增后每名被试的训练和测试样本数如表1 所示。

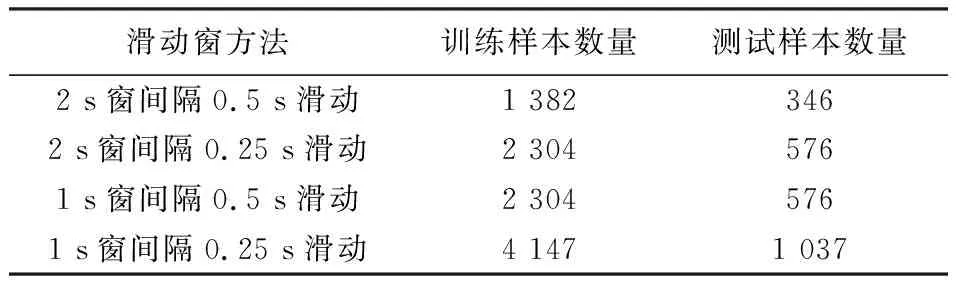
表1 BCI IV 2a数据集扩增后每名被试的样本数量Tab.1 The number of samples per subject after amplification of the BCI IV 2a dataset

3 运动想象脑电分类算法实现

3.1 脑电数据转换及图表示

将多导联MI-EEG数据每个导联定义为图中的一个节点, 导联之间的关联定义为边, 构成图G=(V,E)。 由于各个节点(电极)之间的关联性不同, 所以, 该图是一个包含权重信息的图。 皮尔逊相关系数可用来衡量两个对象之间的相关性, 本文使用皮尔逊相关系数的绝对值来表征不同导联EEG之间的相关性, 作为图的邻接矩阵A。 节点之间的皮尔逊相关系数为

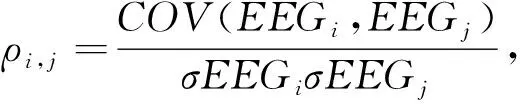
(5)

式中:EEGi和EEGj分别为第i个导联和第j个导联的脑电信号;COV为EEGi和EEGj之间的协方差;σ为标准差。BCIIV2a数据集每名被试脑电数据的邻接矩阵是一个22行22列的实对称矩阵, 将邻接矩阵每行之和作为度矩阵D相应列的列向量, 最后由L=In-D-1/2AD-1/2计算得到MI-EEG图的归一化拉普拉斯矩阵L。 以BCI IV 2a数据集被试A01脑电数据为例, 绘制其邻接矩阵、 度矩阵、 拉普拉斯矩阵的热力图如图4 所示。

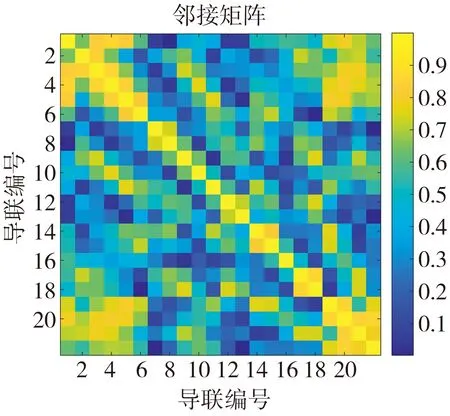
(a) 邻接矩阵

3.2 模型结构与算法实现

本文设计的残差图卷积网络模型架构如图5 所示。 每2层图卷积层添加1个残差连接, 构成1个残差块, 之后添加1个图池化层。 图卷积层采用2阶切比雪夫网络, 图池化层采用EigenPool图池化。 整个网络包含10层图卷积层、 5层图池化层、 全连接层和输出层。

图5 残差图卷积网络模型结构

由于脑电信号本身包含时、 频、 空域信息, 构建的残差图卷积网络能很好地提取其高级特征信息。 将所有脑电导联在滑动窗时长内的采样数据作为一次样本数据, 并且与运动想象4种任务标签对应, 每名被试采集处理得到的全部样本数据按8∶2 随机划分训练集和测试集, 运动想象脑电数据的邻接矩阵作为模型的输入。 输入数据经过5个残差块提取脑电信号的特征, 再由全连接层整合、 映射, 最后输出4类运动想象任务分类的准确率, 并用交叉熵损失函数计算分类损失。

实验采用Python编程, 模型搭建使用TensorFlow框架, 在NVIDIA GeForce GTX 3050Ti GPU上进行训练和测试, 模型计算复杂度较低, 测试运行时间较快。 通过消融实验进行滑动窗、 图卷积层数、 图池化层数、 以及残差块数量的模型优化, 参数设置及优化如表2 所示。

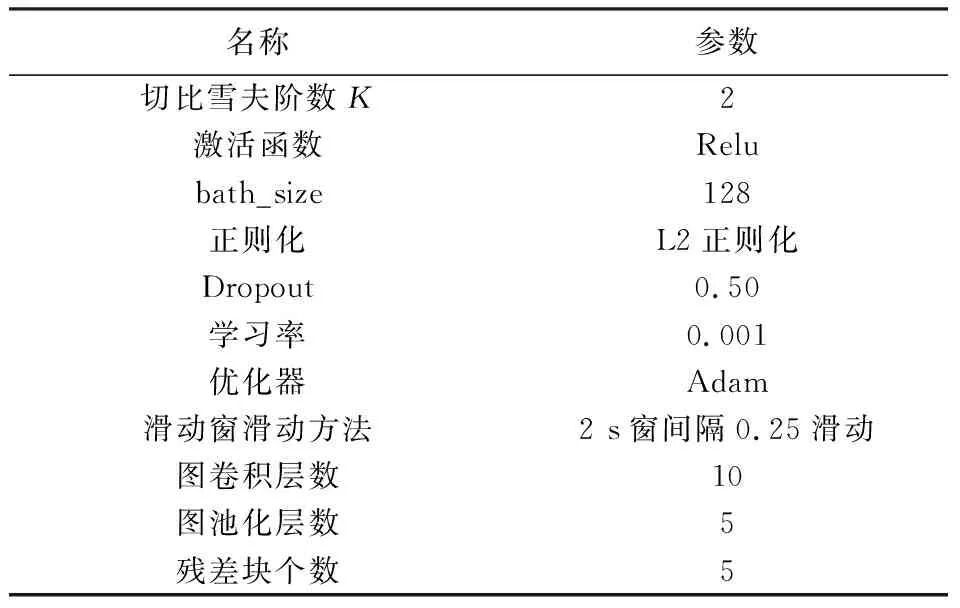
表2 模型参数设置及优化Tab.2 Model parameter setting and optimization

以BCI IV 2a数据集的被试A01为例, 模型训练和测试的准确率及损失曲线如图6 所示。

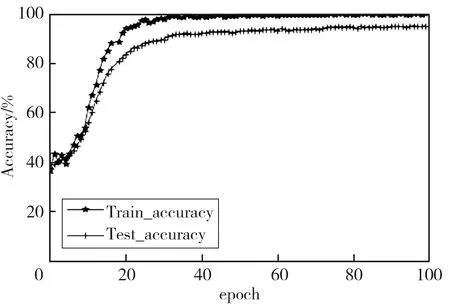
(a) 准确率曲线

从图6 可以看出, 在迭代80轮之后, 测试集的准确率和损失都趋于平稳。 本文实验设置训练和测试迭代轮数为100, 模型能取得稳定的收敛效果。

3.3 模型性能分析

以BCI IV2a数据集被试A01和BCI III IIIa数据集被试K3b为例, 左手、 右手、 双脚、 舌头4类运动想象任务分类结果的混淆矩阵如图7 所示。

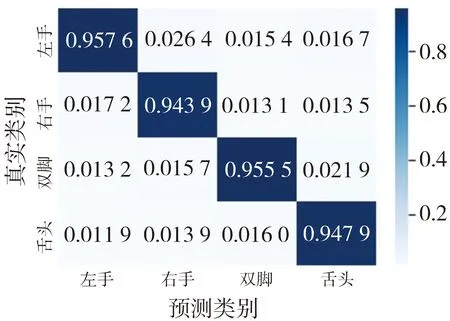
(a) 被试A01分类结果混淆矩阵

基于混淆矩阵计算BCI IV2a数据集9名被试运动想象任务分类结果的平均准确率和Kappa系数如表3 所示。

表3 BCI IV2a数据集每名被试的分类结果Tab.3 Classification results for each subject in BCI IV2a dataset

此外, 本文模型对BCI III IIIa数据集3名被试运动想象任务分类结果的平均准确率和Kappa系数如表4 所示。

表4 BCI III IIIa数据集每名被试的分类结果

结果表明, 本文模型用于运动想象脑电分类时, 在BCI IV2a数据集得到93.84%的平均分类准确率和0.917 1的平均Kappa系数, 在BCI III IIIa数据集得到96.39%的平均分类准确率和0.953 5的平均Kappa系数。 较高分类准确率表明模型可有效区分4类运动想象任务, 获知被试的运动意图; 较高的Kappa系数表明模型对4类运动想象任务的预测结果和实际分类结果几乎完全一致。 此外, 从混淆矩阵结果看模型在两个公共数据集上都取得较好的分类性能, 表明本文提出的残差图卷积网络模型具有较好的泛化能力。

3.4 与其它方法对比

为验证本文方法在运动想象任务分类中的优势, 选取在BCI IV2a和BCI III IIIa数据集上的其他方法与本文方法进行对比如下:

CNN+LSTM[14]: 一种将CNN和LSTM结合的深度学习网络。 CNN和LSTM共同提取MI-EEG的时域特征, 再进行分类。

TSCNN[15]: 一种基于时空特征学习的卷积神经网络。 对带通滤波后的EEG, 设计时空维度上的卷积, 提取MI-EEG的时空特征; 用 2 层二维卷积对EEG的时空特征学习并解码。

GCN[5]: 将GCN用于运动想象任务分类。 根据多电极EEG的相关性建立脑电数据的图结构, 提取EEG时频特征作为输入, 经过GCN进行节点特征聚合学习谱域特征, 再通过全连接层输出分类结果。

AMFGCN[6]: 一种融合注意力的多维特征图卷积网络。 根据电极分布的非欧空间特性构图, 用时空、 频空双分支框架, 融合注意力机制从图中学习EEG的时频空信息, 并捕获各维度的关联信息进行分类。

LAFFN[16]: 一种基于改进的注意力机制和张量分解法的轻量级特征融合网络。 将通过 ESRGAN 进行数据增强后的数据集送入 LAFFN 进行分类。

CSP/Hilbert +SVM[17]: 一种基于CSP、 Hilbert和SVM的运动想象脑电信号特征提取与分类算法。

OVO-CSP+SVM[18]: 一种基于通道频率选择的EEG识别方法。 通过OVO-CSP提取滤波后的运动想象脑电特征向量, 再用SVM分类。

本文与其它方法在BCI IV2a数据集上每名被试的分类准确率、 Kappa系数对比结果如表5 所示。

表5 不同方法在BCI IV2a数据集的分类性能对比Tab.5 Comparison of classification performance of different methods on BCI IV2a dataset

本文与其它方法在BCI III IIIa数据集上每名被试的分类准确率、 Kappa系数对比结果如表6 所示。

表6 不同方法在BCI III IIIa数据集的分类性能对比Tab.6 Comparison of classification performance of different methods on BCI III IIIa dataset

由表5 和表6 可知, CNN+LSTM方法仅提取MI-EEG的时域特征, 分类性能因此受限, 取得76.62%的平均准确率。 TSCNN方法从MI-EEG中提取时空特征, 并结合 2 层二维卷积联合学习, 充分挖掘了原始EEG蕴含的时空信息, 平均分类准确率提高到80.09%。 GCN方法将图卷积网络应用到MI-EEG分类中, 提取不同节点EEG的时频特征和节点间关联空间特征, 取得80.9%的平均分类准确率, 但模型较浅, 提取的特征信息有限。 AMFGCN方法用双分支框架从EEG转换的时空图和频空图中同时提取时频空多维特征信息, 并结合注意力机制和全局特征聚合模块, 捕获EEG在各维度的关联特征, 相较于GCN其平均分类准确率提高到85.74%, 但其模型较浅, 提取脑电深层信息能力有限, 且数据处理复杂。 LAFFN方法用ESRGAN进行数据增强, 基于注意力机制和密集连接的轻量级特征融合网络, 可有效利用中间卷积层提取的特征, 取得91.58%的较高平均分类准确率。 CSP/Hilbert +SVM和OVO-CSP+SVM方法都是先用手工方法提取脑电信号特征, 再用机器学习分类, 分别得到83.7%和86.85%的平均分类准确率, 其性能不及深度学习方法。

本文方法的优势在于将谱域图卷积和残差学习结合, 设计较深的残差图卷积网络, 从全脑空间关联中提取深层有价值的EEG特征信息, 且有效避免了模型出现梯度爆炸和网络退化问题。 分层图池化的降维作用让深层模型复杂度和参数量降低, 能加快模型训练速度, 提高模型测试准确率。

4 结 语

论文提出一种残差图卷积网络模型, 根据脑电电极的天然非欧空间分布, 构建图结构并计算电极之间的相关系数, 用来表征脑电节点空间信息和电极间相互关联信息。 将图卷积神经网络和残差学习结合, 提取运动想象脑电信号深层特征信息的同时, 避免出现网络退化。 将分层图池化方法运用到模型中, 提取图节点特征和局部结构信息并生成图表示, 减小模型复杂度和参数量。 仿真实验结果取得了较高的分类准确率和Kappa系数, 可较好地实现4类运动想象任务分类, 获知被试运动意图。 由于该图模型是基于单个被试进行训练和测试的, 未来仍需结合迁移学习进一步深入研究, 找到适用于跨被试运动想象任务分类的通用模型。