车床尾座同轴度误差快速高精度测量方法研究

吴祖冲, 余厚云, 许晓伟, 游嘉凯, 孙 筱

(南京航空航天大学 机电学院, 江苏 南京 210016)

车床主要由床身、 主轴箱、 尾座、 溜板和导轨等组成[1-2], 如图1 所示。 在加工过程中, 由于车床振动会造成尾座与床身的连接螺栓发生松动[3], 同时刀具和人为因素产生的径向力也会引起尾座的平移和倾斜, 从而形成车床尾座与主轴之间产生较大的同轴度误差, 导致轴类零件加工时, 两端圆柱面直径超差, 难以控制零件的直线度和圆柱度, 从而严重影响钻孔、 扩孔、 攻丝的精度, 最终降低车床的加工精度[4]。 因此, 在车床使用过程中, 必须严格控制车床尾座与主轴间的同轴度。

图1 车床尾座同轴度测量原理示意图Fig.1 Schematic diagram of lathe tailstock coaxiality measurement principle

目前, 可用于车床尾座同轴度误差测量的方法主要有打表法[5-6]和移动关节臂测量[7-8]等。 受制于表杆的长度, 打表法无法测量长距离尾座的同轴度, 并且测量效率低下, 测量过程易受表杆形变的影响, 测量精度低。 移动关节臂虽然测量过程较为简便, 但该方法通过三爪卡盘夹持标准轴来模拟基准轴线。 卡盘夹持存在较大误差, 且标准轴的长度有限, 因此, 该测量方法也难以达到较高精度。 同时, 该方法成本较高, 受限于关节臂长度也无法满足大跨度同轴度测量要求[9]。

本文利用激光良好的准直特性, 提出以激光束作为媒介, 由PSD测量各截面处的激光光斑中心坐标, 通过测量拟合的方法分别得到车床主轴轴线和尾座轴线, 在此基础上, 计算出车床尾座的同轴度误差[10-11]。 相对于传统打表法, 本测量方法将一组同轴度实验的测量时间缩短至10 min左右。

1 系统测量坐标系的建立

如引言中图1 所示, 车床尾座同轴度测量系统主要由准直激光器、 激光测距传感器和光电测头组成。 激光器装夹于车床主轴的三爪卡盘内, 光电测头则安装在尾座上, 测量激光束投射在测头PSD传感器上的光斑坐标。 激光测距传感器则用于测量光电测头沿车床导轨移动的轴向位置。 其中光电测头结构如图2 所示。

图2 光电测头结构图Fig.2 Structure of photoelectric probe

首先, 光电测头保持不动, 激光器绕车床主轴旋转一周, 光电测头测量这一周的激光光斑坐标并拟合得到中心点, 即为车床主轴轴线与当前测量截面的交点。 移动尾座的套筒测量多个截面, 可进一步拟合得到车床主轴轴线; 然后, 保持激光器不动, 光电测头绕车床尾座孔轴线旋转一周, 测量并拟合得到尾座孔轴线与当前测量截面的交点。 轴向移动尾座的套筒并测量多个截面后, 可评定出车床尾座相对于主轴的同轴度误差。

由上所述, 被测轴线与基准轴线是分别测量并拟合得到的, 在评定同轴度误差时需要将二者统一到同一个坐标系下。 为此, 本系统建立了世界坐标系和测头坐标系。

如图1 所示, 将车床尾座固定于导轨上的测量位置, 根据激光测距传感器读数设置光电测头的初始位置。 令PSD的二维坐标系为oxy, 测头坐标系OXYZ以PSD二维坐标系原点o为原点O, 测头坐标系OX与OY轴平行于PSD的二维坐标系, 为ox与oy轴, 指向三爪卡盘的方向定义为OZ轴的正方向, 此时, 双轴倾角传感器测得的初始旋转角为α0。 以在光电测头初始位置的测头坐标系为世界坐标系。

测量过程中, 由于PSD传感器通过安装夹具使其光敏面与尾座轴线垂直且光电测头是通过尾座的套筒移动, 所以, 光电测头是沿着尾座轴线即世界坐标系Z轴移动的。 所以, 测头坐标系在运动中只存在相对于世界坐标系Z轴的旋转和平移, 因此, 需要确定任意时刻两坐标系之间的旋转角和平移量。 如图3 所示, 在任意测量位置i处, 倾角传感器测得的旋转角为αi, 激光位移传感器测得的距离值为di(i>0), 即测头坐标系相对于世界坐标系存在绕Z轴的旋转角Δα和沿Z轴的平移量di, 其中Δα=αi-α0。

图3 系统坐标系与测头坐标系位置关系示意图Fig.3 Schematic diagram of position relationship between system coordinate system and probe coordinate system

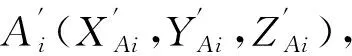
(1)

2 同轴度误差测量

2.1 光斑轨迹中心坐标测量

PSD测量的激光光斑中心是光斑的能量中心, 与光斑的形状和尺寸无关。 激光光斑的中心提取精度影响光斑轨迹中心坐标精度, 即影响主轴轴线或者尾座轴线与PSD所在截面的交点坐标精度, 由于需要一圈轨迹点拟合光斑轨迹中心, 因此, 激光光斑中心的提取精度对光斑轨迹中心的坐标影响较小。 由于激光器装夹于车床主轴三爪卡盘上时难免会存在激光束与主轴轴线之间的偏移和倾斜, 从而导致在激光器绕车床主轴旋转的过程中, 激光束所形成的空间轨迹是以主轴轴线为中心的一个圆锥或单叶双曲面, 其中异面直线和其绕主轴轴线旋转形成单叶双曲面轨迹, 如图4 和图5 所示。

图4 准直光束与主轴轴线的位置关系图Fig.4 Position relationship between collimated beam and main axis

图5 准直光束绕主轴轴线旋转轨迹图Fig.5 Track of collimated beam rotating around the main axis

不论是圆锥还是单叶双曲面, 任意正截面均为封闭圆形, 其圆心也落在旋转轴线上, 圆心即为主轴轴线与某一截面的交点, 因此, 准直激光只作为测量媒介, 三爪卡盘的夹持精度不影响同轴度测量结果。 本文采用PSD传感器测量任意测量截面的光斑轨迹, 即PSD感光面与圆锥面或单叶双曲面的相贯线; 针对旋转轨迹为圆锥的情况进行理论仿真, 单叶双曲面类似。 由于PSD传感器的感光面与基准轴线并不垂直, 因此, 传感器实际测量的是圆锥或单叶双曲面的斜截面, 此时截面轨迹应为封闭椭圆, 且椭圆中心并不落在旋转轴线上, 如图6 和图7 所示。

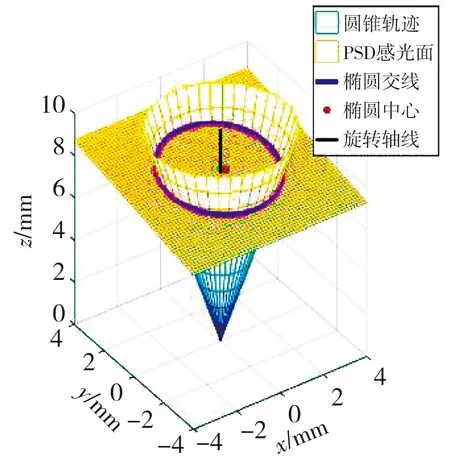
图6 基准轴线测量误差仿真三维图Fig.6 3D simulation diagram of datum axis measurement error

图7 基准轴线测量误差仿真二维图Fig.7 2D simulation diagram of datum axis measurement error

因此, 理论上利用多个斜截面的中心去拟合轴线, 存在一定的误差, 但是根据实验发现, 激光与车床主轴轴线的夹角一般在1°以内, PSD感光面与车床主轴轴线基本垂直, 其误差也在1°以内, 被测截面的位置与车床三爪卡盘之间距离小于1 000 mm, 测量位置处圆锥正截面的光斑轨迹圆半径r小于3 mm。 在此实验条件下, 仿真得到光斑轨迹中心坐标与对应位置正截面圆心坐标相差在1 μm以内, 所以, 将实际光斑轨迹的中心坐标直接作为正截面圆心坐标。

本文采用基于随机抽样一致性(RANSAC)[12-14]的最小二乘椭圆拟合算法, 拟合截面中心坐标。 RANSAC随机抽样一致性算法是一种参数估计法。 根据RANSAC算法的基本思想, 利用RANSAC算法改进了直接最小二乘拟合椭圆的方法, 具体实现步骤如下:

1) 设置迭代次数m与内点(误差在阈值内的点)个数最大值t。 定义模型中的距离, 并设置其阈值为d;

2) 在PSD传感器测得的所有光斑重心坐标点中, 随机抽取6个坐标点, 并利用最小二乘法LSA进行椭圆拟合;

3) 根据定义的距离模型, 遍历剩下的所有坐标点, 求各点到拟合的椭圆之间的距离, 若距离小于阈值d, 则标记为内点, 遍历完成后, 统计内点的总个数c;

4) 比较内点总个数c与理想内点个数最大值t, 当c>t时, 结束迭代过程并记录所有内点, 再利用最小二乘法对最优内点集合重新进行椭圆拟合, 得到最终需要的椭圆参数;

5) 若ct或迭代次数达到设定值m, 结束建模。 若由于迭代次数达到设定值m而结束建模, 那么取m次迭代中内点个数最多的集合重新进行拟合, 得到最终需要的椭圆参数。

算法流程图如图8 所示。

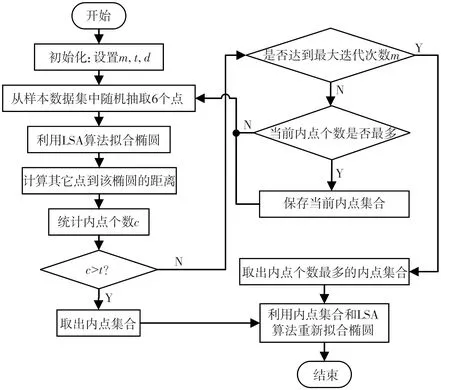
图8 椭圆拟合改进算法流程Fig.8 Flow chart of improved ellipse fitting algorithm

对于本系统而言, 距离模型的定义如图9 所示。 设椭圆O为从数据集中随机抽取的6个数据点, 是经最小二乘法拟合得到的, 点A为数据集中任意点, 连接AO与椭圆交于点B, 定义线段AB为本模型中的距离, 并将距离阈值d设为0.02 mm。

图9 距离模型的定义Fig.9 Definition of distance model

2.2 主轴轴线测量与同轴度误差评定

通过移动尾座的套筒, 将光电测头移到不同测量截面, 测得多个截面的光斑轨迹中心坐标。 主轴部分测得的轨迹中心坐标依据最小二乘原理得到的一条主轴轴线[15]。 根据国标《GB/T 1182-2018》和机械行业标准《JB/T 7557-1994》, 同轴度误差采用最小包容区域法评定。 如图10 所示, 尾座部分截面中心点分布在主轴轴线附近, 最小包容区域即以主轴轴线为中心线, 包围空间分布的尾座孔各截面中心点的最小圆柱体, 该圆柱体的直径为同轴度误差。

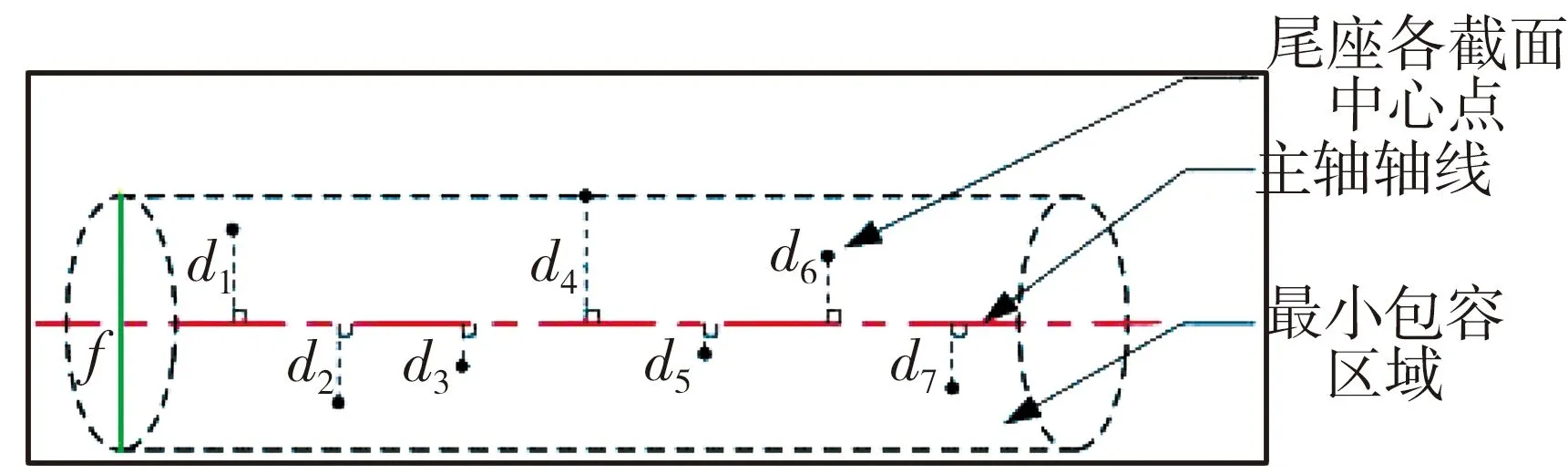
图10 最小包容区域示意图Fig.10 Schematic diagram of minimum containment area

通过计算尾座部分各测量截面交点到主轴轴线的距离, 本文取所有距离中最大距离的两倍作为同轴度误差值, 其中尾座孔任意测量截面的交点Ci(xi,yi,zi)到主轴轴线的距离

(2)

式中:P=(x0,y0,z0), 表示主轴轴线经过的基点坐标,Q=(m,n,p), 表示主轴轴线的方向向量。 则系统所求的同轴度误差为

f=2×max{di}。

(3)

3 实验与分析

3.1 椭圆拟合算法验证实验与分析

为验证2.1节中的基于RANSAC的最小二乘法拟合椭圆的拟合效果, 采用原始光斑轨迹坐标的实验数据, 通过在原始数据的基础上分别添加随机误差为±0.05 mm, ±0.1 mm, ±0.15 mm, ±0.2 mm, ±0.25 mm, ±0.3 mm, ±0.35 mm, ±0.4 mm的误差点。 针对上述添加不同误差值的数据集, 分别采用两种算法拟合得到的椭圆中心坐标分布结果如表1 所示。

表1 两种椭圆拟合方法得到的中心坐标Tab.1 Central coordinates obtained by two ellipse fitting methods

由表1 可以清晰看出, 基于RANSAC的最小二乘算法可以根据设定的距离阈值将大于阈值的外点剔除, 从而提高椭圆拟合的精度。

3.2 同轴度测量实验与分析

根据上述测量原理和测量系统坐标系的建立, 本系统拟定的基本测量流程如图11 所示。 将激光准直模块和光电测头分别装夹于车床三爪卡盘和尾座套筒内, 如图12 所示。

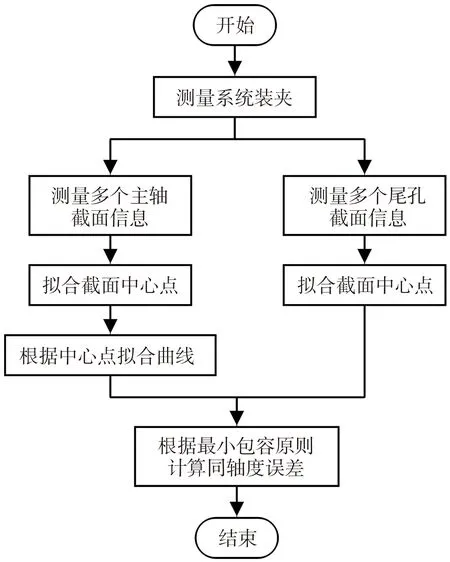
图11 同轴度测量流程Fig.11 Flow chart of coaxiality measurement

图12 车床尾座同轴度测量系统主要部件实物组成图Fig.12 Physical composition of main components of lathe tailstock coaxiality measuring system

调节尾座位置, 使光电测头分别位于距激光准直模块500 mm和750 mm位置。 在每个位置处, 选取5个测量截面, 相邻截面间距离为25 mm, 测量范围0～100 mm。 在两个测量位置分别进行10组同轴度测量实验, 实验数据如表2 所示。 500 mm处和750 mm处的拟合轴线为图13(a)和图13(b)所示。 以750 mm处的主轴轴线为例, 10组主轴轴线的直线方程参数如表2 所示。 表2 中x0,y0,z0为直线经过的基点的坐标,m,n,p为直线方向向量。 从数据可得, 主轴轴线重复性误差小于0.01 mm。

表2 同轴度测量实验数据Tab.2 Experimental data of coaxiality measurement

根据表2 测量结果, 绘制同轴度误差曲线, 如图14 所示。

图14 不同位置处10组同轴度误差变化曲线Fig.14 Variation curve of 10 groups of coaxiality errors at different positions

两个位置的同轴度误差不一致, 这是因为车床主轴与尾座不同轴, 两者之间距离变化导致两个异面直线距离变化。 在两个位置处的10组实验中, 同轴度测量结果的极差均小于0.01 mm, 两组测量结果的标准偏差s为0.002 2 mm和0.001 mm。 根据莱以特准则, 测量结果中未出现异常值, 则测量系统的A类不确定度优于0.003 mm。

计算同轴度误差测量不确定度的关键在于基准轴线和尾座孔截面中心的位置变动量。 系统不确定度主要来源于PSD的误差、 倾角传感器测量误差、 主轴和光电测头的径向跳动误差、 尾座套筒移动的直线度和激光位移传感器测量误差。 根据资料, PSD传感器误差为0.001 mm, 该误差的概率分布近似于正态分布; 根据资料, 倾角传感器分辨率为0.005 5°, 精度0.01°, 实际使用中旋转角的测量值存在±0.01°的波动, 且概率分布近似于均匀分布; 对于普通级车床, 其定心轴颈的径向跳动为0.01 mm, 对于本系统所用的光电测头, 经过打表测量, 其径向跳动为0.003 mm; 根据同轴度实验数据来看, 尾座套筒移动直线度为±0.003 2 mm, 假定该误差的概率分布为均匀分布; 根据资料, 激光位移传感器测量误差为±0.8 mm, 且测量值服从均匀分布。

基于测量模型和上述输入量的概率密度, 采用蒙特卡洛法对系统的测量不确定度进行评定。 评定过程基于Matlab平台, 分别对500 mm和750 mm位置处测得的第1组同轴度数据分别进行不确定度模拟计算, 试验次数为100 000次, 得到的概率密度分布直方图分别如图15(a)和图15(b)所示。 对于500 mm处的仿真计算结果, 同轴度误差的平均值为0.191 mm, 标准不确定度为0.002 7 mm, 包含概率为95%的置信区间为 [0.185 7,0.196 2]; 对于750 mm处的仿真计算结果, 同轴度误差的平均值为0.289 mm, 标准不确定度为0.003 2 mm, 包含概率为95%的置信区间为 [0.282 8,0.295 2]。 这为系统测量结果的可信度及可靠性提供了理论依据。

(a) 500 mm处

4 结 论

1) 提出了一种基于激光准直和光电检测的车床尾座同轴度误差快速高精度测量方法。 适用于能够旋转的轴系同轴度的测量, 对于测量时不能转动的轴系, 尚未找到理想的测量方法。 设计了相应的测量装置并进行实验验证。 测量装置的A类不确定度优于0.003 mm, 每组实验的同轴度误差的极差在0.01 mm以内, 解决了高精度、 高效率检测车床主轴与尾座的同轴度误差问题。

2) 利用随机抽样一致性算法改进最小二乘拟合椭圆算法, 通过随机抽取样本点进行拟合并标记误差点的方法, 构建了误差点检测和剔除机制, 实验结果表明, 该方法能够很好地剔除误差点, 大大降低了测量中的随机误差, 并提升了拟合速度, 提高了椭圆拟合的抗干扰能力, 实现了椭圆中心点快速高精度拟合。