超高精度测光观测及数据处理分析方法*

石亚卿,王炜,赵景昆

(1 中国科学院国家天文台 中国科学院光学天文重点实验室, 北京 100049; 2 中国科学院大学天文与空间科学学院, 北京 100101; 3 中国科学院国家天文台 中智南美天文中心, 北京 100101) (2022年1月14日收稿; 2022年4月7日收修改稿)

自Mayor与Queloz[1]于1995年通过视向速度法首次发现第一颗太阳系外行星飞马座51b以来,天文学家已发现了4 935多颗系外行星(截至2022年2月22日,数据来源于https:∥exoplanetarchive.ipac.caltech.edu/)。飞马座51b是一颗典型的热木星,即:公转周期少于10 d,温度高于1 000 K的气体巨行星。随着样本数量的飞速增长,系外行星及其大气的观测研究发展迅猛,使得系外行星的形成和演化等理论也日趋成熟。

Charbonneau等[2]于2002年利用哈勃空间望远镜对热木星HD 209458b展开多次凌星观测,首次探测到太阳系外行星的大气,揭开了探测和研究行星大气的序幕。在随后的20年里,利用空间望远镜哈勃、斯皮泽及大型地面光学红外望远镜,对大量系外行星的大气开展了不同程度的研究。现已在系外行星大气中探测到约20种原子及分子[3],如在HD 189733b, HD 209458b等系外行星大气中探测到水、一氧化碳及钠[4-8];在 KELT-9b上探测到大气中可能存在铁(Fe)及钛(Ti)或者钛离子[9]。系外行星领域的研究重点已逐渐由搜寻探测转移到通过高精度测光和光谱观测来测定系外行星大气的性质和成分,并对行星性质进行限制。而这些高精度的观测为系外行星的化学组成、大气温度轮廓、 云/霾分布、大气动力学及大气逃逸等理论提供了良好的限制,并极大促进了行星大气模型、行星大气光谱模型等研究的飞速发展[10]。

系外行星大气信号非常暗弱,且淹没在其主星的辐射中。对于热木星,行星大气的透射信号大约是恒星信号的10-3,发射信号大约为其10-4,对于更小更冷的行星,信号更弱。因此,要对系外行星大气进行有效的研究,需要观测数据的精度优于10-4。本文定义精度优于10-4的测光为超高精度测光。空间望远镜如哈勃[11]、斯皮泽[12]、开普勒[13]、TESS[14],因不受地球大气及观测时长影响,仪器设备条件相对稳定,测光及光谱精度较高,可接近或优于10-4。例如对超热木星WASP-12b,TESS 获得的测光精度达到10-5量级[15]。但空间望远镜时间宝贵,大部分系外行星大气的观测还是依赖于地面望远镜。

而地基望远镜因受地球大气抖动、天气变化、连续观测时长、望远镜指向等因素的影响,即使在测光条件良好的情况下,采用传统的观测模式和数据处理方法也很难达到或优于10-3的绝对测光精度和优于10-4的较差测光精度。

为通过超高精度测光方法探测和研究系外行星大气,地面望远镜——加拿大法国夏威夷望远镜(Canada-France-Hawaii telescope,CFHT) 开发了“凝视”观测模式,通过4个子窗口实时高频监测视场中4颗参考星的位置,快速调整望远镜姿态,从而维持望远镜指向的高精度和稳定性[16]。CFHT望远镜是一台口径为3.6 m的光学/红外望远镜,其配备的WIRCam红外照相机拥有20′的视场,由4块HAWAII2-RG探测器组成,是世界上最大的天文红外探测器之一,也是用于探测系外行星热辐射的重要地基望远镜之一。采用凝视观测模式之后,星像中心在探测器上位置移动很小,最多不超过2个像素。Croll等[17-18], Wang等[19], Martioli等[20]的工作都利用 CFHT 成功获得10-4量级的测光精度,从而对热木星大气给出了重要的观测限制。其他大型望远镜,包括Very Large Telescope (VLT) ,Hale 5 m望远镜,也开展了类似的观测研究[21-22]。然而,即使采用了 “视观测模式”,并不代表一定能获得超高精度,还需要优化观测模式、较差测光算法、模拟并扣除红噪声,才能最终达到10-4量级的测光精度。

高精度的时域测光不仅适用于行星凌星探测、行星大气研究,也可用于恒星活动性、 星震、双星系统等多种研究。不同科学目标所要求的时间采样率、测光精度不同,但总体来说,精度越高,可获得的信息越丰富越准确。影响测光精度有多重因素,能够模拟它们并消除各种因素带来的影响,使得测光精度接近理论极限,对科学研究是极为重要和关键的。

本文首先以系外行星凌星观测为例,介绍超高精度测光的基本原理和方法;然后以从CFHT的宽视场红外相机WIRCam获得的超热木星WASP-103b在J与Ks波段的两次次食观测为例,讨论如何设计观测并通过后期的数据处理和分析,实现亚毫星等的测光精度。

1 测光误差及超高精度测光

1.1 时序测光误差分析

探测系外行星大气信号的主要方法是凌星法和次食法。当行星位于恒星面与望远镜之间,即凌星时,行星本身对恒星面的遮挡造成系统的总亮度下降,下降幅度正比于行星恒星半径平方比。行星大气也会对恒星光造成一定的吸收,其吸收深度取决于连续谱和谱线吸收深度,与行星大气的性质,包括温度密度轮廓、分子混合比等密切相关。测量行星凌星时不同波长处的吸收深度,即透射光谱,可定量研究行星大气的性质。

而当行星位于恒星背面,即发生次食时,行星被恒星遮挡,整个系统的总亮度有微弱的下降。这个下降的亮度即反映了行星的亮度,是行星本身的热辐射及反射的恒星辐射被行星大气吸收和散射之后的亮度。因此,行星大气本身的发射光谱与行星的大气参数也密切相关,可用于研究行星大气性质。要获得这两种光谱,都需对凌星系统开展数小时或几十到上百次曝光的时域观测,通过对比整个系统在凌星/次食时的亮度与凌星之外的亮度,获得透射或发射光谱信号。

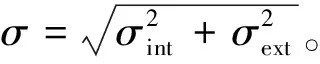
单次测光的理论误差一般由测光孔径内的信噪比决定,而信噪比(signal-to-noise ratio, 简称 SNR)有如下计算公式

(1)

其中:Np为总的由目标星光子转换成的电子的数目;而Nb是总的背景噪声电子数,包括了天光背景对应的电子数,探测器读出噪声和暗电流。

假设Nb=0,要实现SNR=10 000,对应精度约为 10-4,需要总的星光电子数为108。对于K=12.5等的恒星,利用3.5 m口径、总系统效率为0.3的望远镜,需要积分时间20 min才能在探测器上收集到108个电子。而实际上Nb>0,因此要实现超高精度,目前只能针对亮星,即K<12.5。也因此,在高精度测光中遇到的情况是光子噪声占主导地位,而光子噪声是随机噪声,或称白噪声,服从泊松分布,无法消除或减弱。天光背景、探测器读出电路和暗电流带来的噪声,也无法扣除,只会在积分时间增加、光子数增加的情况下,其相对影响逐渐变小。因此,要想获得接近于极限的测光精度,首先要尽量增加有效积分时间,其次是需要在观测时尽量减少红噪声,在数据处理时通过各种算法削弱它们的影响。这是实现超高精度较差时序测光的关键。

1.2 观测策略和仪器设置

首先,从科学目标出发,选择合适的观测波段,提高一定观测时间内可累计的光子数以及行星信号的相对强度。例如,为了对系外行星热辐射进行有效的观测,一般在近红外波段开展观测。因为系外行星在近红外波段热辐射相对较强,而恒星辐射在近红外波段相对较弱,选择近红外波段观测更有利于探测行星热辐射信号。也可针对与拟探测分子的光谱特征,选择特定的波段。比如,为探测水分子信号,一般选择中心波长为1.6 μm的H波段,为探测CO或者CO2,中心波长为2.21 μm 的K或者Ks 波段为最佳的宽带波段。

其次,优化观测设备和观测策略。一般对系外行星大气的观测,要覆盖行星凌星或次食的全部时间,以及前后1 h以上的基线观测,因此需要连续观测4～8 h,具体时间取决于凌星时长。长时间的时域观测过程中,台址天文条件包括视宁度会有波动,大气质量会有连续的变化。考虑到这些变化在视场内是近似同时同量的,可以通过与参考星的对比从而消除或减弱上述变化带来的测光误差。因此需要视场中有多颗亮度和颜色与目标星接近、且不存在短周期光变的恒星作为参考星。而实际上,天气的变化可能会是局部的,视场中不同位置的大气质量也存在微小的变化,多个探测器芯片拼接而成的相机中的各个芯片也存在读出电路和暗电流速率等因素的差别,最好选择位于同一个芯片且角距离较小的星作为参考星。

探测器芯片中各个像素对入射光的响应不同,像素内不同位置对于光子的响应也不同,即:intra-pixel sensitivity variation, 以下简称IPSV[23]。此外,探测器中往往有不少有缺陷的像素,包括失去感光性的死像素以及读数比本底高的热像素。由于望远镜指向存在一定的误差,恒星在视场中有小的移动,星像在探测器上也将移动。即使忽略大气变化等外部因素导致的影响,假设望远镜接受到的光子数不变,探测器通过光电效应转化而成的电子数也会发生变化,从而导致测量出来的恒星星等或亮度发生变化。传统的利用平场改正的方法,可以消除像素间的不均匀性,但精度难以优于1%,而且此方法无法改正IPSV。因此要实现高精度测光,望远镜的指向精度或者相机的稳像精度必须很高。除此之外,对于较亮的系外行星主星,利用米级望远镜1 s曝光都可使得感光像素进入非线性区甚至饱和,这种情况下的测光是不准确的。如果采取1 s或更短曝光时间,考虑大视场望远镜的探测器读出时间一般需要20 s以上,这样的观测效率无疑太低。举例来说,假设曝光时间1 s,读出时间20 s,则观测5 h实际对目标源的积分时间只有14 min左右,获得的总光子数远不足以实现1‰的精度。因此,需要将星像或者点扩散函数(PSF)变大,将入射光子分布在多个像素,从而避免落入探测器的非线性区或饱和区。需要强调,光斑直径增大使得光斑覆盖的范围成平方增长,在同样的指向误差情况下,光斑覆盖像素变化率显著减小,因此能显著减少像素不均匀性和IPSV带来的误差。当然,实际测量中,测光过程中包括的像素越多,读出及背景噪声就越多,从而使SNR降低。不过,对于我们的亮星观测,因为是光子泊松噪声占据主导,背景噪声相对较弱,因此采用此方法可以显著提高观测精度。考虑到这些因素之后,利用大量的实时观测的参考星对系统噪声进行模拟并矫正,就可以获得亚毫星等(10-4)级别的较差测光精度。

1.3 数据处理和分析方法

对于较差测光的数据处理,主要分以下2个步骤。首先要对获得的原始数据进行基本的图像处理,包括扣除本底,进行平场改正和暗电流改正。在此过程中,要对死像素进行标注。然后针对目标星和参考星分别进行一系列孔径值的孔径测光。孔径大小的设定要非常谨慎,既要保证孔径足够大以覆盖星像所有流强,又要使孔径尽可能地少吸收天光背景噪声或读出噪声,通常外孔径为内孔径的1～2倍。传统的测光是要通过对比不同孔径值时的测光结果确定最佳孔径,整个视场或者部分视场采用同样的孔径值。这样的方法忽略了不同的星有不同的最佳孔径,也没有考虑最佳孔径随时间的变化,因此精度无法满足要求。

经过测试,发现目标星和每一颗参考星应设置不同的孔径值以获得最佳的光变曲线。如果观测条件好,大气稳定,测光时星像大小稳定,可设定孔径大小为常量。如果星像大小不稳定,则需设定孔径大小随时间变化以达到更精确的测光。实际操作中,我们获得了目标星和参考星多个孔径值下在每一次曝光的星等,也就获得了多个孔径值下的光变曲线。然后利用 Everett 和 Howell[24]提出的方法,获得初步的较差光变曲线。寻找此光变曲线基线部分与观测时间、大气质量、星像中心位置、视宁度等参数的关系并扣除,可以减弱红噪声带来的影响。也可采用高斯过程,用非参数化的方式估计红噪声的贡献并扣除。

参考星的初选主要由恒星的亮度来决定,一般选择与目标星亮度在±2等范围内的恒星。这样初选出来的参考星不一定都适合。因为颜色可能不同、或者离目标星比较远、或者其在探测器上所处的位置有大量异常像素。因此,有些参考星的原始光变曲线与目标星和其他参考星相差较大,或者趋势不同,可以逐步剔除出去,最终获得一个最优参考星组合。实际分析过程中,参考星组合与孔径值对测光的影响可能存在耦合,因此需要多次迭代,找到最佳的组合,使得基线数据的弥散最小。下面以实际的数据为例,具体描述如何实现超高精度测光。

2 观测设备和观测数据

2.1 观测设备和模式

使用的设备是CFHT上的宽视场近红外照相机设备WIRCam,它是地基望远镜中具有探测系外行星次食信号能力的重要设备之一。此相机由4块2 K×2 K的近红外探测器拼接而成,相邻探测器的间隙为 45″,总视场大小为20.50′×20.50′。

为实现超高精度测光,CFHT 团队开发了凝视观测模式。在此模式下,可选择视场中的4颗星作为指向参考星,通过快速读出和快速的星像中心分析,计算视场偏移量,迅速调整望远镜姿势或者快摆镜位置,使得望远镜指向稳定,星像基本位于探测器视场固定的位置上。同时,对望远镜进行较大程度的散焦,以避免目标星或参考星所在的像素进入非线性区甚至饱和。Croll通过 CFHT 上的 WIRCam 设备利用这一模式成功探测到3颗热木星以及1颗褐矮星的次食信号并达到0.014%～0.040%的测光精度。

2.2 目标星观测数据

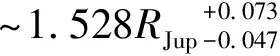
利用CFHT的WIRCam,在2015年对热木星WASP-103b进行J与Ks波段的总计11 h的次食观测。6月9日在J波段进行持续5.25 h的凝视观测,望远镜散焦量为1.8 mm。总共曝光55次,覆盖包括次食及其前后1 h左右的基线时间,大气质量在1.02～1.37。每次曝光分为若干个积分时间为15 s的子曝光以提升读出效率,降低暗电流影响。首次曝光包含9次子曝光作为测试,其余的曝光调整为12次子曝光。目标星视星等为12.1 mag,K波段星等为10.7 mag,选择该星场内约100颗星作为初选参考星,它们的视星等范围在8～14 mag。

5月28日进行的是Ks波段观测。然而,观测时天气并不理想,观测数据误差较大,无法开展科学研究。因此,重新处理了Delrez. L在2014年5月20日利用相同设备同一波段的数据。此次观测望远镜进行了2 mm的散焦,总共曝光1 092次,每次曝光积分时间5 s。

3 数据处理与分析

3.1 主要步骤

较差测光是一种测量目标星相对于参考星亮度变化的数据分析方法。为达到 10-4的测光精度,在传统的较差测光步骤中加入了更多的误差分析和误差扣除,以提高数据精度。具体包括以下几个主要的关键步骤:

1)图像预处理

利用WIRCam专用的数据预处理程序I’iwi 2.1,进行初步数据处理,包括标记饱和像素点、非线性校正、参考像素扣除、暗场扣除、平场扣除、标记坏点及天光背景扣除。I’iwi程序把标记为坏点的像素赋值为0,如果坏点包括在测光孔径或天光范围内,就会影响测光结果,因此,利用坏点周围的4个像素进行插值,用于估算坏点像素的计数。

2)参考星初选

选择视场内星等及颜色接近目标星且无明显光变的恒星(Δm～±2 mag) 作为候选参考星。在图像中查看这些参考星所在的位置,剔除距离探测器边缘100像素以内的,剔除星斑范围内包括较多坏点和热点较多的,尽量选择与目标星在同一个探测器芯片里的参考星。以J波段数据为例,通过上述过程,筛选出10颗参考星。

3)孔径测光参数考虑及孔径测光

开展孔径测光需要设定目标星的中心位置、孔径值、天光背景环的内外半径等参数。其中,测光孔径的大小对测光精度有着重要影响。既要保证孔径足够大以覆盖全部星像,又要尽量减少天光背景噪声和探测器噪声,因此其数值不能太大,也不能太小。在数据处理过程中,以从图像中得到的星像的半高全宽乘以一个大于1的因子作为初始孔径值。并以其为中值,±5像素范围内的一系列孔径值进行测光计算,相邻的孔径值相差1个像素。

因望远镜散焦,恒星星像呈多纳圈形状,难以准确确定星像中心位置。因此,将扣除天光背景后的图像与二维高斯函数卷积,还原成为中间高周围低的亮斑之后,再利用IDL程序CENTORID测定星像中心位置。天光背景参考区域是一个圆环,内、外孔径分别为1.5倍和2.5倍测光孔径。以此区域内像素的平均值作为天光背景。然后,利用IDL天文程序包APER测量目标星和参考星每次曝光的亮度值及测光误差,从而得到原始光变曲线。

4) 获得目标星光变曲线

对于获得的光变曲线,先通过目视剔除光变曲线弥散很大、变化趋势与大部分星不一致的参考星(参见图1(a)不同颜色所代表的参考星光变曲线,黑点组成的光变曲线代表目标星)。这些星本身可能具有光变,或者与目标星的颜色相差较大,因此大气质量变化带来的趋势不同。对于目标星和剩下的参考星,针对每一条光变曲线,通过 Sigma-clipping方法,迭代3次扣除超过中值2倍标准差的测光点,获得光变曲线的中值,然后将光变曲线归一化到中值。将目标星和所选用的参考星的归一化光变曲线以其标准差为权重取平均,得到平均光变曲线(图1(a)中黑色折线)。取平均的目的是要降低各个参考星的随机误差带来的对光变曲线的影响。目标星的光变曲线除以平均光变曲线再归一化,即得到扣除了大部分红噪声的较差光变曲线(参见图1(b))。完成了这一步,光变曲线的弥散大概在10-3量级。

5)模拟并扣除红噪声

光变曲线中除无法扣除的随机噪声,还存在不可忽略的红噪声。它与时间等参数相关,且对地基观测的精度有很大影响。为了扣除红噪声,采用多参数的多项式拟合,包括目标星星像中心在x方向和y方向相对于第一次曝光时位置的偏移以及观测时刻等参数。同时,利用公开的 IDL 程序EXOFAST[29],对光变曲线进行拟合。EXOFAST采用马尔科夫蒙特卡洛采样法,结合Mandel 和 Agol[30]给出的理论光变曲线(简称 MA 模型)对观测光变曲线开展后验分析,获得对行星和恒星相关参数的估计,包括次食深度、行星平衡温度等。此时得出的后验参数并不重要,重要的是拟合的残差。图1(b)中玫红色空心三角形是第 4 步得到的较差光变曲线,蓝色实线是得到的红噪声,黑色圆点是扣除红噪声之后的光变曲线,红色实线是模型给出的次食光变曲线。图1(c)中的黑色数据点及误差棒代表每36个数据点合并之后的平均值及误差,红色实线是对它们的最佳拟合。扣除红噪声之后,次食光变明显可见。

6)确定最佳测光孔径及最佳参考星组合孔径值的选择对测光结果(包括星等或亮度及其误差)极为重要,而参考星的选择对较差光变曲线的数值及误差有重要影响。孔径和参考星选择的优劣主要由拟合光变曲线的残差的均方根 (root mean square, RMS) 的大小来衡量。此过程最为复杂,是实现10-4精度的关键细节,详情见下节。

3.2 参考星及测光孔径值最优选择

经过步骤1～3,获得了目标星和参考星在不同测光孔径值时的较差光变曲线。取决于选择的孔径值数量和参考星数量,光变曲线的数量一般超过100。目标星的光变曲线要扣除平均光变曲线才能得到较差光变曲线,而参考星的组合数目非常大。本小节主要以测量WASP-103b的次食深度为例,描述如何找到最佳光变曲线,以及最优的孔径值和参考星组合。

首先,用MA模型去拟合或模拟上述得到的每一条光变曲线,获得最优或最可几模型解,从而得到行星次食深度等信息及观测-模型残差的均方根RMS。很自然,光变曲线的优劣由拟合残差均方根来决定,残差越小,光变曲线越好,得到此光变曲线的孔径值和参考星组合就越优。当然,因为光变曲线数目太多(102),其组合数目估计达到或超过104,遍历所有组合是不现实的。举例来说,只考虑单一孔径值,10颗观测参考星中挑出1～10颗作为参考星的排列组合的数目已超过103,若考虑10个以上的孔径值,组合数目远超104。

因此,需对参考星的优劣进行排序。然后从最好的参考星开始,按照优劣先后添加参考星。若排序靠后的参考星的加入导致拟合变差,则此参考星及排序更靠后的参考星都将被剔除。在我们的数据里,这一步排除了2～4颗参考星。我们参考Croll等,排序采用的依据是RMS×β2。其中RMS是目标星利用单独一颗参考星得到的光变曲线与其最可几模型的残差的均方根。校正因子β是一个量化红噪声的参数,其值～ 1代表残留的噪声几乎都是白噪声,值越大代表红噪声越多[31]。通过数据点合并,每N个数据点合并为1个,合并之后的数据数目为M,合并后的残差标准差σN。σN与σwn,N的比值即为β,其中

(2)

反映了在只有白噪声的情况下,N个数据点取平均后的理论标准差。图2展示了σN(虚线)和σwn,N(实线),可以看出一般情况下前者大于后者,因此有β>1。在N较大的情况下,采样点少,可能存在过拟合的情况,因此有少数β<1,此时令β=1。

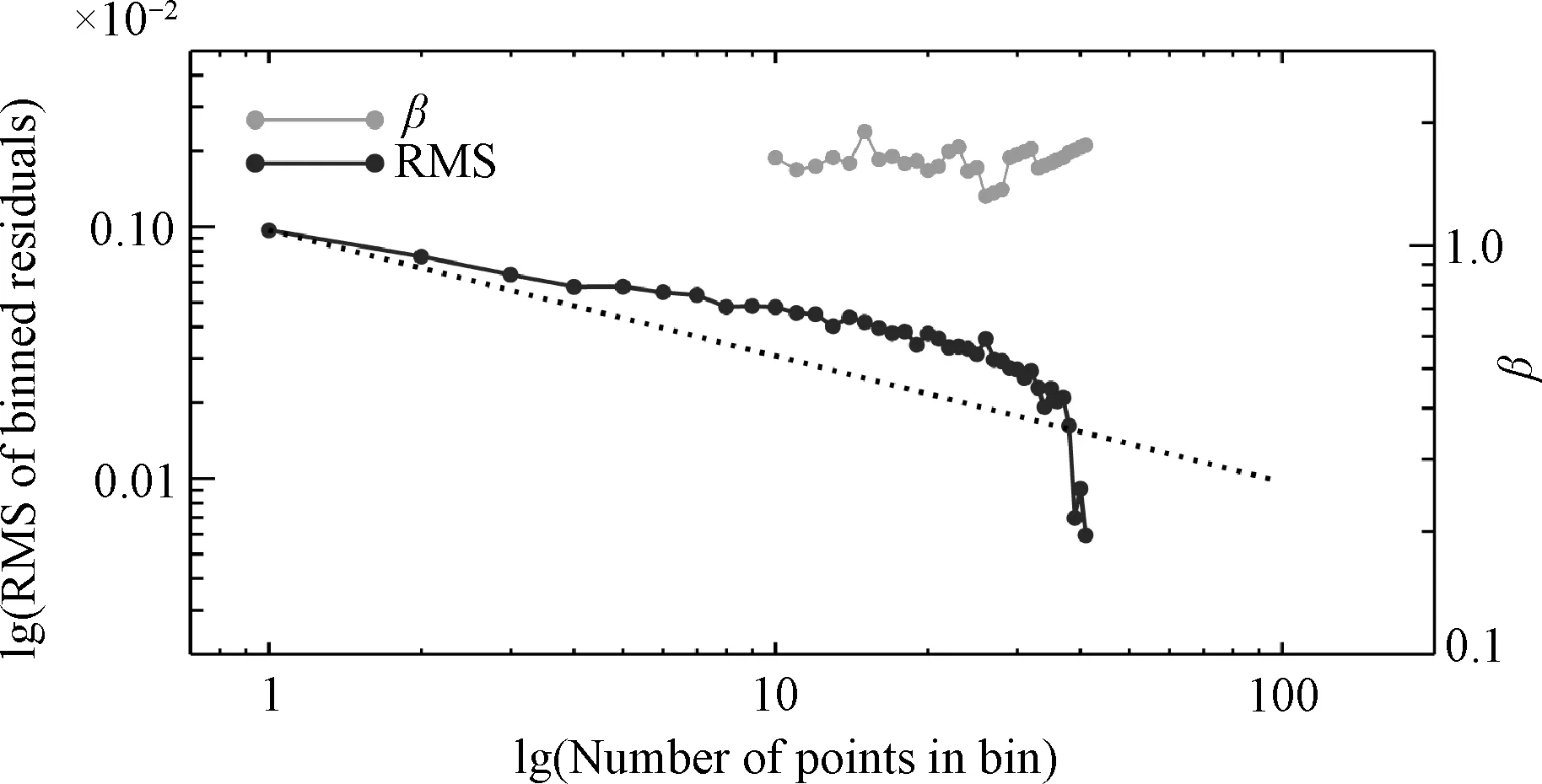
图2 J波段WASP-103b的数据的残差、噪声因子与最可几拟合模型Fig.2 RMS and noise factor β of our residuals to the best-fit model for the various data sets

如前所述,孔径值的设定应尽量减少背景噪声的影响并覆盖恒星尽可能多的光强。对于本文分析的CFHT数据,总共选择15个孔径尺寸,即26～40个像素。尽管最佳的测光孔径值可能随观测时刻有变化,但其变化不大,因此在实际分析过程中,对于同一颗星,在一次次食观测中采用同样的测光孔径。参照Croll等的方法,改变测光孔径和参考星数目,就可以得到RMS×β2二维分布,并根据其最小值得到最佳测光孔径和参考星数目。图3展示了WASP-103b的J波段光变曲线在不同的参考星数目和测光孔径值下得到的RMS×β2的等高线,可以明显看出参考星数目为4、测光孔径值为38像素的组合为最佳组合。因为RMS×β2数值小,且变化小,为便于展示和分析,图中实际画的是5+lg(RMS×β2)线。

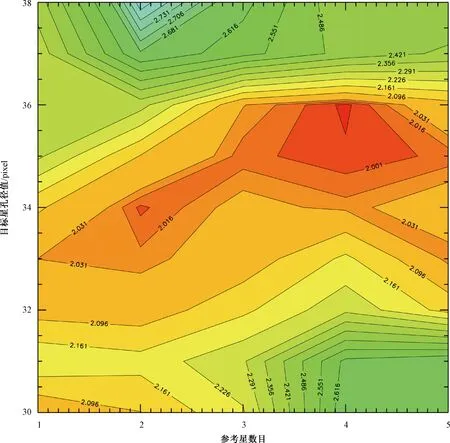
图3 J波段WASP-103b光变曲线的5+lg(RMS×β2)等高线图Fig.3 The contour map of the light curve of WASP-103b in J-band

在上述过程中,目标星和参考星用的是同样的孔径值。而实际上,因目标星和参考星亮度不同,二者在探测器上的星像大小并不严格相同,因此进一步研究了目标星和参考星的孔径值独立变化是否能够得到更好的拟合。首先,对同一颗参考星在不同孔径值条件下计算 RMS×β2,得到每颗参考星较小的3个RMS×β2对应的孔径值。我们发现,对于大部分参考星,改变其孔径值能够得到更小的RMS×β2,因此每一颗参考星的孔径值也应该作为搜寻RMS×β2最小值的因变量。然而,这样的组合的数目是孔径数目Naper的参考星数目Nref次方。对我们的J波段数据来说,前者是18,后者是5,大约189万种组合。遍历所有的孔径组合并不现实。

因此,类似于前文对参考星优劣的排序,我们对每一颗参考星的孔径值也进行了排序。参照前文得到参考星排序的方法,固定目标星孔径(38像素),固定参考星组合(4 颗),变化某一颗参考星的测光孔径,得到一系列RMS×β2,根据RMS×β2数值确定测光孔径的排序,并选择最小的3个RMS×β2值所对应的孔径值作为局部最优孔径值。同样,固定参考星测光孔径,也可得到目标星的3个局部最优孔径值。把这些局部最优孔径值组合起来,用于寻找全局最优的参数组合。

参考星组合的确定需要基于统一孔径条件下的结果。先按照统一孔径得到的RMS×β2值对参考星进行排序,依次进行个数由2～6颗参考星递增(5种情况)的误差估算及模型拟合,11个孔径大小进行55种组合(如图2,得到参考星数目与孔径大小组合的等高线图),从而确定最佳个数选择。最后,将选出的几颗参考星及它们对应的最佳3个孔径大小与目标星的3个孔径大小进行组合,确定全局最佳组合。

4 讨论和结论

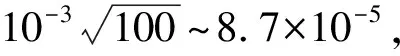
为实现超高精度测光,观测设备方面最重要的是要有良好的指向精度和大幅延展的星像,后者主要通过散焦实现。然而,新的研究和测试表明,利用匀化器件(比如散光器diffuser等)能够实现更好的测光精度,对天气、望远镜指向等要求更低[32]。观测方面,首先需要选择合适的波段,尽量多观测次食以外的基线部分。本文讨论的数据在观测开始及结束时误差较大,可能是由于大气扰动及观测设备不稳定。为避免引入额外的误差和拟合偏差,在拟合过程中剔除了这些误差较大的数据点,浪费了大概20%～30%的数据。基线数据对于扣除红噪声非常重要,因此建议尽可能增加基线观测的时间。

数据处理和分析方面,关键在于如何选择最佳的参考星和测光孔径,以及模拟并扣除红噪声。我们提出,把参考星和目标星的孔径值作为自由变量,相对于使用统一的孔径值,可以将测光精度提高1倍左右。需要指出的是,利用此方法,测量主食食深,也可获得类似精度,也可采用高斯过程等方法模拟并扣除主食光变曲线中的红噪声。