用单摆测量液体粘滞系数的实验设计与讨论*

张声遥 曾志强 柳福提 宛俊杰 陈 鹏

(宜宾学院理学部 四川 宜宾 644000)

液体流动时,平行于流动方向的各层流体的速度如有不同,各层之间就有摩擦力产生,称为粘滞力.液体的这种性质称为液体的粘性.液体的粘滞系数是表征液体粘滞力强弱的重要参数.粘滞力只有在液体内存在相对运动时才表现出来,通常采用“落球法”来测量液体的粘滞系数[1].“落球法”利用小球在液体中达到匀速运动时所受粘滞力与浮力、重力的平衡关系以及斯托克斯公式F=-6πrηv,只要测量小球的收尾速度、直径、密度及液体的密度等量即可测量液体的粘滞系数,原理简单.但实验时小球下落过程时间较短,很难保证小球达到匀速运动,要重复实验取出小球又很不方便,容易产生油液浪费与油污.文献[2-6]提出利用阻尼振动来测量空气的粘滞系数并进行了实验与讨论,受其启发,本文利用单摆在液体中的阻尼振动来测量液体粘滞系数,既可解决上述“落球法”测液体粘滞系数实验的不足,也可以生动直观地显示液体的粘滞阻力对小球运动的影响,加深学生对物理概念与规律的理解,培养学生的创新意识与能力.

1 实验原理

如图1所示,将一单摆置入待测液体中,使单摆偏离平衡位置一定角度,并在无初速度的状态释放,单摆将在液体中来回摆动,如同在空气中一样.

由于液体的粘性,单摆在摆动过程中将会受到液体粘滞阻力的作用.设小球的半径和运动速度分别为r和v,则小球在流体中所受的粘滞阻力可写为

F=-6πrηv

(1)

其中比例系数η为粘滞系数,负号表示粘滞阻力的方向和小球运动的速度方向相反.根据图1的受力分析,小球还受到重力和摆线拉力的作用,其受到的合外力矩为

M=-(mgθ+6πrηv)l

(2)

其中m表示小球的质量,g是重力加速度,θ是摆线偏离竖直方向的角度,l是摆长.根据转动定律可得单摆的运动方程为

(3)

(4)

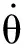
令

c=6πrη

则式(4)可以变为

(5)

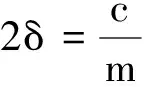
(6)

此方程的解有3种情况.

(1)若δ<ω0,方程的解为

θ(t)=Ae-δtcos(ωt+φ0)

(7)

(2)若δ>ω0,方程的解为

(8)

这种情况称为过阻尼振动.

(3)若δ=ω0,方程的解为

θ(t)=(c1+c2t)e-δt

(9)

称为临界阻尼振动.

在本实验中,单摆的运动是欠阻尼运动,所以其运动方程的形式应为方程(7).而且实验中单摆无初速度释放,可知φ0=0和A=θ0,其中θ0为单摆开始摆动时的初始角位移.因此可得单摆的振动方程为

θ(t)=θ0e-δtcosωt

(10)

根据此公式,可知角振幅随时间变化关系为

θA(t)=θ0e-δt

当t=nT(n=0,1,2,…)时,有

θA(nT)=θ0e-δnT

(11)

由此可得

(12)

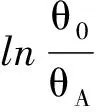
(13)

可求出液体的粘滞系数η.

2 实验设计与实现

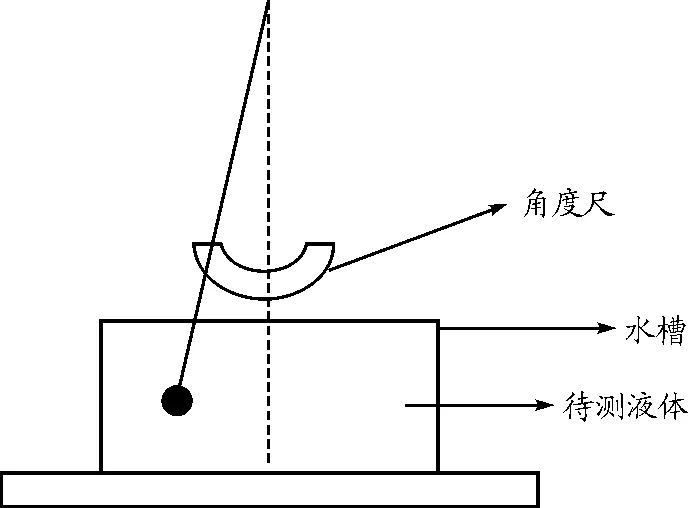
图2 实验装置原理图

图3 实验装置的实物图

3 实验结果

为验证以上论述的实验设计,我们测量了空气、水和菜籽油的粘滞系数.首先,实验测得小球的直径d=16.906 mm和质量为m=16 g.

3.1 空气的粘滞系数测量

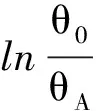
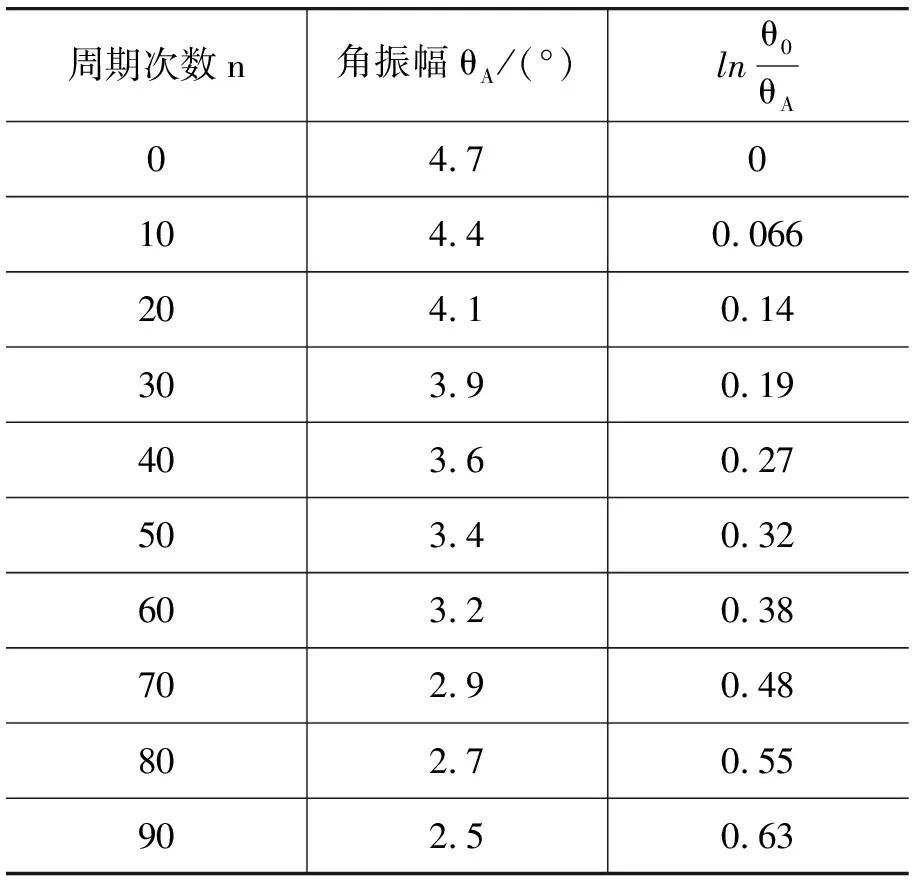
表1 空气中单摆的角振幅随周期的变化关系

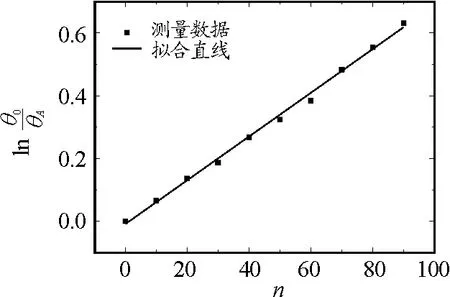
图4 空气中单摆的-n线性拟合

3.2 水的粘滞系数测量

将单摆置入水中进行阻尼摆动,测得单摆的角振幅随周期的变化数据如表2所示.将表2数据绘于图5中可以看到数据具有明显的线性关系.同样利用线性拟合可以得到直线斜率为k=δT=0.2,同时测得摆动周期T=1.75 s,根据公式(13)算出水的粘滞系数为η=2.30×10-2Pa·s.

表2 水的粘滞系数测量数据

图5 水中单摆的-n线性拟合

3.3 菜籽油的粘滞系数测量

如上同理,利用单摆对菜籽油的粘滞系数也进行了测量.测量数据如表3所示.表3中数据绘于图6中,拟合后的图线展示出良好的线性关系.数据拟合直线的斜率为k=δT=0.98,同时测得摆动周期T=1.85 s,由此可以算出菜籽油的粘滞系数为η=1.06×10-1Pa·s.

表3 菜籽油的粘滞系数测量数据

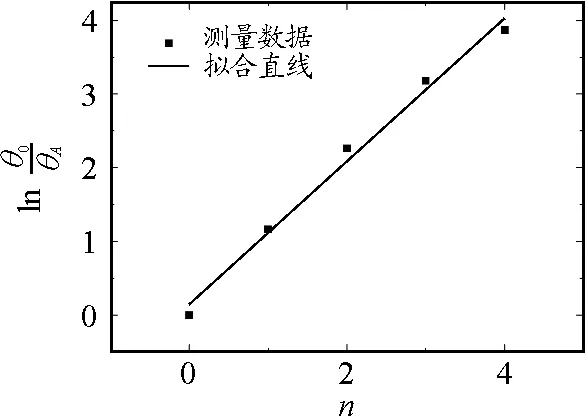
图6 菜籽油中单摆的-n线性拟合

4 实验结果讨论

4.1 实验结果不确定度计算

通过计算测量值的不确定度,可以判断实验结果的准确性.从式(13)可以看出粘滞系数测量的不确定度由m、r和δ决定.其中δ又与角振幅随周期变化关系的拟合直线的斜率k与单摆周期T的测量值有关.根据误差理论,m、r和T的测量值的不确定度可由下式决定

(14)

其中Δ表示仪器的最小刻度值.因此根据电子秤、螺旋测微器和秒表的最小刻度可以计算m、r和T的测量值的不确定度.k的不确定度计算公式为

(15)

(16)

其中um、ur和uT分别表示m、r和T的不确定度.根据式(15)～(16)可以计算出空气、水和菜籽油的粘滞系数测量值的不确定度分别为4×10-4Pa·s,

1.53×10-2Pa·s和5.50×10-2Pa·s.从计算结果看菜籽油的粘滞系数测量误差相比于空气和水更小,因为菜籽油的粘滞系数更大.

4.2 实验结果与传统测量结果的比较

以上实验结果显示,利用单摆的阻尼振动测得室温下空气、水和菜籽油的粘滞系数分别为8.78×10-4Pa·s、2.30×10-2Pa·s和1.06×10-1Pa·s.而依据传统落球法测得水和菜籽油的粘滞系数分别为2.2×10-2Pa·s和1.08×10-1Pa·s,其中空气的粘滞系数无法用落球法测量.比较两种方法的测量值可以看出,两种方法在精度和误差上相当,且随着液体粘度的增加,两种方法的测量结果趋于一致.通过查阅文献得知在室温下水的粘滞系数的标准值为1.01×10-3Pa·s,而菜籽油大约为5×10-2Pa·s[7].因此,不管是用单摆还是落球法测量都比标准值要大.原因之一是摆线系在铁架的一端摆动过程中有附加摩檫力、以及细线与空气之间粘滞力的存在,引起测量数据增大;另一方面是实验中所测液体的粘滞系数相对较小,导致湍流容易影响小球的运动,所以实验结果出现了一些误差.

5 总结

本文设计了利用单摆的阻尼振动来测量液体粘滞系数的实验方案,并以空气、水和菜籽油作为被测对象进行了实验,测出了室温下空气、水和菜籽油的粘滞系数.该方法在精度上与传统方法相当,且操作更简单,不会因为重复取出小球而产生油液浪费与污染.而且,与传统方法比较,该方法具有能测量气体粘滞系数的优点.此外在实验中观察到单摆在液体中通常会摆动较长时间,从而在教学上有利于学生观察,有效提高教学质量.