物理学家视角的模型建构层级设计*

陈伟孟

(中国人民大学附属中学 北京 100080)

马朝华

(北京市海淀区教师进修学校 北京 100097)

1 关于模型建构

核心素养中的科学思维主要包括模型建构、科学推理、科学论证、质疑创新等要素.模型思维是一种重要的科学思维,为了描述客观事物的运动规律,科学家往往把研究对象抽象为理想模型,突出问题的主要方面,忽略次要因素,建立理想化的“物理模型”.我们通常可以把物理的模型建构分为:建立模型、分析模型、验证模型等过程.高中物理课程标准将科学思维中的模型建构分为五级水平,如表1所示.

表1 科学思维中模型建构水平划分

其中,水平二是学业水平合格性考试的要求,水平四是学业水平等级性考试的要求.在物理模型教学中,通过学习物理模型的建立及其应用,可使学生逐步认识模型的设计依据,建立模型的方法,从而初步掌握建模方法.

理想模型是为了便于研究问题而对研究对象进行理想化抽象的过程.实际问题往往比较复杂,影响的因素很多,直接研究它们会比较困难.科学研究中运用这种方法,人们就可以用模型来表示研究对象,使得研究变得简单、有效,从而便于人们去认识和把握问题的本质.理想模型在现实中并不存在,但是通过它可以对实际问题进行本质探讨,并得到有价值的结论.物理学习中通过抽象方法建构的理想化模型有很多,如表2所示,按照研究对象来看可以分为质点、点电荷、单摆、弹簧振子、理想气体等模型,按照研究过程来看可以分为匀变速直线运动、匀速圆周运动、简谐运动和碰撞等模型.实际上,具体问题的研究往往是对象模型和过程模型组合研究的过程,比如质点的匀变速直线运动和弹簧振子的简谐运动.

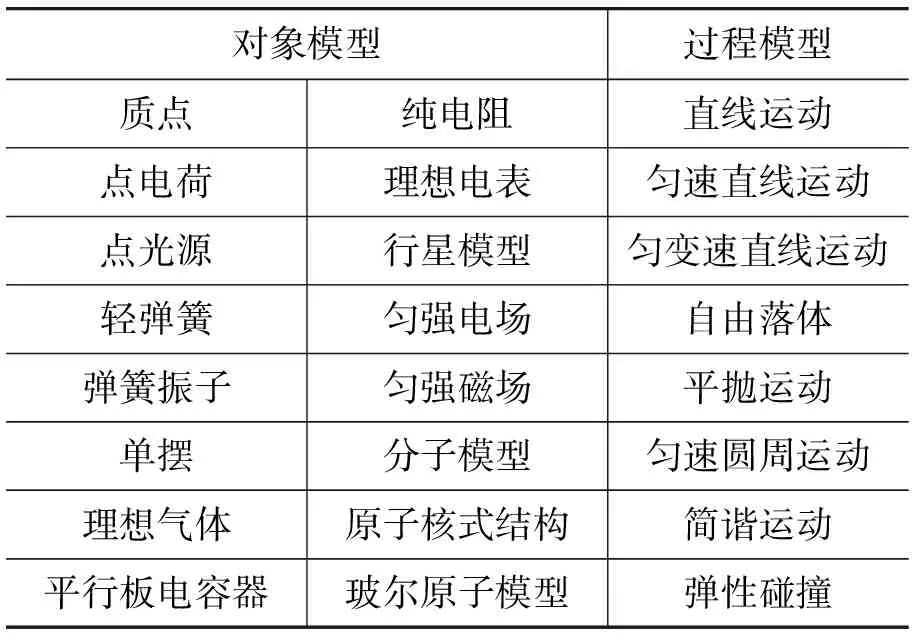
表2 一般物理模型的分类

如图1所示,模型建构既是用理想模型去描述表示实际问题的过程,也是将实际问题抽象为理想模型的过程.物理学科核心素养要求具有建构理想模型的意识和能力,能正确运用科学思维方法,具有批判性思维的意识,能基于证据大胆质疑,从不同角度思考问题.每当遇到新问题时,物理学家们总是试图建立一个物理模型加以解释.高中物理学习过程中,学生会遇到各种物理模型,这是对自然世界认识过程的提炼.因而,模型建构不仅是处理问题的手段,更是人类认识这个世界的方式.在物理学中发展起来的建模方法已经渗透到其他科学领域和社会的各个方面.

图1 模型建构过程

我们在认识、解决某个实际问题时,总要把实际问题抽象成一个简化的模型加以解决.例如研究一列火车从北京到南京的运行问题时,尽管火车各部分的运动各不相同,很复杂,但对于我们要研究的问题而言,可以把火车各部分运动的差别忽略,甚至火车的长度都可以忽略不计.在这种情况下,我们可以用一个有质量的点来表示火车的运动,称为“质点”.但要研究车轮上某点的运动,则不能把火车看成一个点.因此,把一个实际问题抽象成与之对应的理想模型总是有一定的适用条件的.突出问题的主要方面,忽略次要因素,抽象出研究对象或研究过程的本质特征,进而对其进行研究.

以物体的运动为例,物理学家大致是通过3个层次进行力学解释的,并由此体现3个方面的物理学思想.第一个层次是提出物理实在的基本构成的假设性构型.通过设想物质基本单元的构型和相互作用来回答“物体究竟是怎样构成的和怎样运动的”问题.质点就是作为组成物体的物质粒子理想模型,被看作最基本的物质单元,其他物体可以看作由质点构成的质点系.然后再设定质点之间的相互作用,由此建立质点的运动理论.第二个层次是设定物理实在的假设性力学模型.通过从模型演绎得到的运动变化来回答“物体的运动及其变化究竟是怎样发生的”问题.自由落体运动、匀速圆周运动和简谐运动等就是这样的力学模型.第三个层次是建立分析动力学的运动方程.通过数学抽象把运动规律上升提炼为用符号表示的数学方程,来回答“物体的运动规律究竟具有怎样的普遍性”的问题,也被称为数学模型.从质点构型到物理模型再到抽象符号表示,从本体论思想到物理建模再到数学综合的思想,是物理学家研究力学现象的3个层次.

2 单体模型建构

【案例1】某同学将质量m=0.60 kg的篮球从距地面高度h1=1.5 m处由静止释放,篮球与地面碰撞后反弹高度h2=1.2 m.设篮球始终在竖直方向做一维运动,不计空气阻力,取重力加速度g=10 m/s2.

模型分析：本案例对应学业质量水平四的内容,通过模型建构层级的具体情境划分,能将实际问题中的对象和过程转换成所学的熟悉物理模型.模型建构中体现着层级的设置,对应着学生问题认识和问题解决能力的水平.

研究对象为篮球,“篮球从距地面高度h1=1.5 m处由静止释放”.篮球在此处仅仅做一维的平动,一般运动物体可视为质点的条件是“该物体的大小远远小于其位移的大小,或者该物体仅仅做平动运动”,不考虑篮球的转动,因此可视为质点,按照质点模型来分析.

研究过程为匀变速直线运动和碰撞.篮球在整个过程中做自由落体、匀加速和匀减速等匀变速直线运动,同时与地面碰撞时涉及机械能的损失,因此属于一般碰撞.

建模层级(1)：假设篮球每次与地面碰撞损失的机械能相同,篮球通过与地面多次碰撞反弹,反弹高度会越来越低,最终停下来.求由静止释放到最终停下来,篮球与地面碰撞的次数n.

问题解决(1)：

篮球一次碰撞损失的机械能为

ΔE=mgh1-mgh2=1.8 J

篮球与地面碰撞的次数

建模分析(1)：假设篮球每次与地面碰撞损失的机械能相同.学生通过观察篮球高度的变化,能够直观发现篮球碰撞过程中是伴随着机械能的损失的,故该碰撞并非弹性碰撞.每次机械能损失相同,与实际运动情况有联系又有区别,属于机械能减小过程中的最初级的建构.

建模层级(2)：实际上篮球每次因碰撞损失的机械能会随着碰前动能的减小而减小,假设篮球每次与地面碰撞前后的动能之比不变.为了使篮球反弹得高一些,可以通过拍球来实现.

当篮球第一次与地面碰撞后反弹至h2=1.2 m时,该同学向下拍球,要使篮球落地后反弹的高度仍为1.2 m,求该同学在拍球过程中需要对篮球所做的功W.

问题解决(2)：篮球每次与地面碰撞后与碰撞前的动能的比值为

根据动能定理,篮球下落过程

W+mgh2=Ek1

篮球反弹上升过程 -mgh2=0-Ek2

可得

W=1.8 J

建模分析(2)：机械能等比减小.学生结合实际拍球时篮球高度的变化,能够发现篮球碰撞过程中的高度应该是非线性减小的.每次机械能损失不同,但是损失量与篮球碰撞前的动能有关,建立两者之间的关系,接近实际情形并能通过计算解决.对做功的问题并不做恒力或变力的区分,用一般性的动能定理解决问题.

建模层级(3)：在拍球过程中,可以通过改变拍球的作用力大小从而改变拍球的节奏,我们会发现不管是篮球的下落还是上升,有一段过程篮球好像粘在手上一样.这是因为球开始下落的同时向下拍球,手通过接触会对球施加一向下的动力F1;当球反弹上升至某一高度时,手通过接触对球施加一向下的阻力F2,使球和手一起向上运动至最高点.若拍球过程中篮球最大高度始终为1.2 m,手对球的两次作用力均视为恒力,且在上升和下降过程中,球与手作用的距离均为s=0.2 m.请推导F2大小与F1大小之间的关系式,并在图2中画出F2-F1图线,标出图线与横轴交点的横坐标.

图2 F2-F1坐标系

问题解决(3)：根据动能定理,篮球下落过程

根据

可得F2大小与F1大小关系

F2-F1图线如图3所示.

图3 F2-F1图线

建模分析(3)：学生结合实际拍球时篮球高度的变化,能够发现篮球碰撞过程中的高度应该是非线性减小的,采用了等比的方式.每次机械能损失不同,但是损失量与篮球碰撞前的动能有关,建立两者之间的数学关系.做功的角度,将外力做功细化为恒力做功,使得手对篮球的做功问题更直观具体,并且是学生运用已有知识能够解决的问题.

建模层级(4)：若某中学物理研究性学习兴趣小组设计制作了一款传感器手套,他们用该手套测试同学在运球、传球、投篮时手对篮球施加的力的大小.某同学戴着手套原地连续在一维竖直方向练习拍球测试,通过传感器手套得到了手对篮球施加向下的压力F随篮球距地面高度h的变化关系如图4所示.求:拍球时篮球与地面碰撞前后的动能之比.

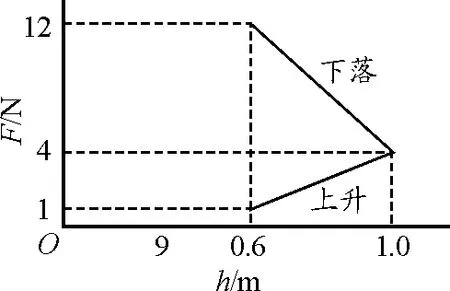
图4 F-h变化关系

问题解决(4)：拍球时是恒力→线性变力做功.随位移线性变化的力做功,与弹簧弹力的做功类似,由恒力功→变力功,通过图像中线性力与位移所围成的面积进行计算解决

建模分析(4)：对做功进行建模的过程中,恒力做功应该是较简单的一种情形,在此基础上联系实际,将恒力做功转变为变力做功.变力做功时,与弹簧弹力的做功类似,进行关联整合,线性恒力做功是学生能够通过公式或图像来计算的,因此在此基础上进行线性变力做功的进阶,从而实现建模层级的进一步提升,更接近实际问题的情境.

3 系统模型建构

【案例2】如图5所示,一条轻绳跨过定滑轮,绳的两端各系一个小球a和b,用手托住球b,当绳刚好被拉紧时,球b离地面的高度为h,球a静止于地面.已知球a的质量为m,球b的质量为3m,重力加速度为g,定滑轮的质量及轮与轴间的摩擦均不计.若无初速度释放球b,则下列判断正确的是( )

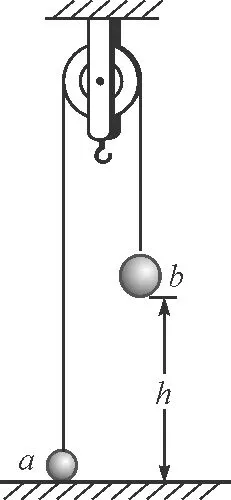
图5 案例2图

B.在球b下落过程中,球b所受拉力大小为mg

C.在球b下落过程中,球a的机械能保持不变

建模分析：

研究对象从单体→二体系统.在一种情形中,将a、b均由静止释放,故a、b在相同时间内运动的距离相等,故轻绳对a做的正功和对b做的负功之和为零,使b减少的机械能完全转移给a,系统机械能守恒.而在另一种情形中,将b托起一定高度释放后,轻绳绷紧的过程中,b在极短时间内减速而a在极短时间内加速从而两者共速.在这个极短过程中,b运动的距离大于a运动的距离,a与b相当于发生了一次完全非弹性碰撞,故细线对b所做的负功大于对a所做的正功,使得b减少的机械能没有完全转移给a,部分转化为细线伸长而产生的内能.

通过以上分析可见:同样是细线连接的两个物体a和b,由于初始状态不同,导致结果相异.其关键就在于对“不可伸长的细线”的正确理解,“不可伸长”决不是绝对不可伸长的意思,而是伸长量相对原长而言可忽略.形变是产生弹力的必要条件,如果轻绳不可伸长,那轻绳中将不会出现弹力.因为绷紧时间极短,导致弹力极大,极大的弹力在极小的位移内做功不为零,进一步导致系统机械能不守恒.

如图6(a)所示,这个装置原型叫阿特伍德机(Atwood machine),是由英国数学家兼物理学家的乔治·阿特伍德在1784年提出的,用于测量加速度及验证运动定律的机械.一个理想的阿特伍德机包含两个物体质量为m1和m2,及由无重量、无弹性的绳子连结并包覆理想且无重量的滑轮.当m1=m2时,无论两物体在何位置、机器处于力平衡的状态.当m1≠m2时,两物体皆以大小相等的加速度做运动.如图6(b)所示,从阿特伍德机衍生出去,我们可以将其与验证牛顿第二定律的实验联系起来,两物体皆以大小相等的加速度做运动,实现认识的关联与整合.

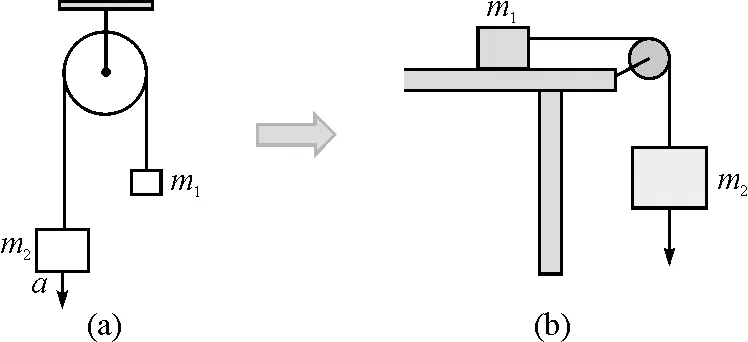
图6 阿特伍德机衍生装置示意图

【案例3】应用物理知识分析生活中的常见现象,可以使物理学习更加有趣和深入.例如人原地起跳时,总是身体弯曲,略下蹲,再猛然蹬地,身体打开,同时获得向上的初速度,双脚离开地面.从开始蹬地到双脚离开地面的整个过程中( )

A.地面对人的支持力始终等于重力

B.地面对人的支持力的冲量大于重力的冲量

C.人原地起跳过程中获得的动能来自于地面

D.人与地球所组成的系统的机械能是守恒的

建模分析：对于质点模型,我们不能仅停留在“一个有质量的点”的理解上.牛顿第二定律的研究对象是一个质点.对于由多个质点组成的系统,在质点的牛顿第二定律基础进一步可以推导出质点组的牛顿第二定律

F=m1a1+m2a2+…+mnan

其中F为质点组所受合外力.

人站在原地起跳时,人获得的机械能是怎么来的?很多学生会下意识觉得来自于地面支持力做的功.如图7所示,可以通过类比进行建模.

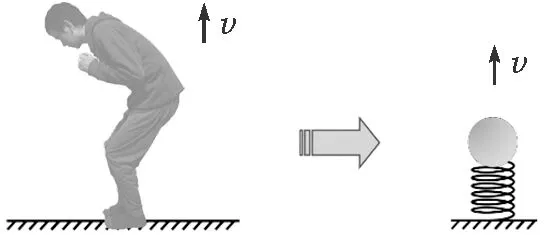
图7 人原地起跳与弹簧组合类比

一小球和一轻质弹簧组合一起,处于压缩状态的弹簧能够将这个组合弹起,这个过程中小球增加的机械能就是弹簧的弹性势能转化而来的.经过思考分析就会发现这个能量不会来自地面,因为这个过程中地面是不动的,其支持力是不做功的.人在起跳的过程中,人不能看成质点,而是由无数个质点组成的系统,人在起跳的过程中,通过系统内力做功把化学能转化为人的机械能.值得注意的是:在人起跳的过程中,由于内力等大反向、且作用时间相等,故内力冲量的矢量和为零,人的动量变化与人的内力冲量无关、只由人所受外力冲量决定,即地面支持力和人的重力冲量共同决定.由此可以看出:质点相关的运动规律是复杂体系运动规律的基础,有了质点这个概念以及建立在质点概念基础上的规律使我们认识复杂系统的运动成为可能.如图8所示的两个人在冰面上互推的过程,就是一个动量守恒而机械能增加的过程,与弹簧的弹性势能转化为两物块的动能类似,这是化学能转化为机械能的过程,也是属于定性分析的过程.

图8 人在水面上互推与弹簧组合类比

【案例4】高压采煤水枪出水口的截面积为S,水的射速为v,射到煤层上后,水的速度变为零,水的密度为ρ,不计水的重力影响.如何求水对煤层的冲力?

建模分析：这是中学物理中另一个常见模型即“流体模型”,是一个更为综合的多体系统模型,我们可以从二体系统过渡到多体系统进行分析,如图9所示.

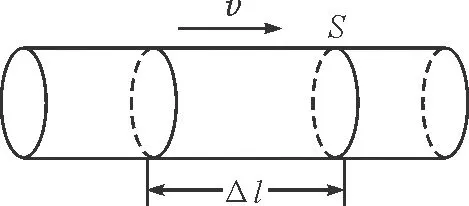
图9 案例4模型

取Δt内与煤发生作用的水为研究对象,其质量Δm=ρSvΔt,对其应用动量定理,得-FΔt=0-Δmv,可得F=ρSv2,故水对煤的冲力F′=F=ρSv2,进一步可求出压强p=ρv2,可见水冲击产生的压强与速率平方成正比.工业上可以用高速水流产生的巨大压强进行金属切割、工业加工等应用,就是所谓的“水刀”.

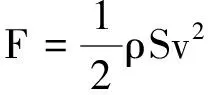
如何看待这两种建构的模型?

这实际上与上述的质点系统模型有关:一段时间内与煤发生作用的流体在减速过程中,相互之间必然有“挤压”的作用力,这种作用力属于这些流体间的内力,与人原地起跳类似,内力做功并不为零.也就是说,在流体与煤作用过程中,并不能把流体看成质点.因此,上述动能定理的表达式中应该还有一项流体内力做功的表达式(内力做功的结果把机械能转化为内能),而动量定理表达式中并没有内力冲量的问题,所以模型二与实际情形是有出入的.相对于判断系统的能量增减,运用动量定理算是属于定量分析的过程.

4 总结

在学生学习的不同阶段,对于同一个模型的理解和认识是需要逐步加深的,可以根据具体的标准和条件进行修正,以更逼近实际问题,这是物理学中一种典型的研究思想方法的体现.人们认识任何事物一般总时遵循着从简单到复杂,由“点”到“面”再到“体”的各个认识阶段的.从质点理想模型入手,逐步修改近似条件,以求得更加接近对实际复杂事物真实面貌的认识.理想化模型源于具体事物又高于具体事物,是感知和思维的产物.模型建构,不仅是我们研究具体问题的手段,也是我们认识这个世界的方式,这是科学认识方式对我们学习的重要启示,在学生学习和教师教学过程中都应充分的重视.