部分剪切连接胶合木-混凝土连续组合梁受力性能分析

彭俊源，王鹏，刘一凡，王永慧，史世伦，韩春秀

（1.昆明理工大学建筑工程学院，云南昆明 650500；2.昆明理工大学城市学院，云南昆明 650500；3.云南民族大学电气信息工程学院，云南昆明 650504）

0 引 言

目前我国大力倡导节能减排及全民环保，为积极配合国家环保政策，推动绿色低碳的生活方式，建筑行业正在通过改革创新以适应新的环保要求[1]。胶合木是一种新型的绿色集成建材，具有环保、低碳、节能等优势，是一种可再生再循环的材料[2]。胶合木结构在西方国家已经有很长的发展历史，从住宅的大门横梁到楼盖主梁，商业和工业用房的梁、柱，再到公路桥以及海洋建筑结构中均能见到胶合木的使用[3]。随着我国经济的发展，低碳环保意识增强，越来越多的人将注意力转移到了木结构上面，进而胶合木也得到了愈发广泛的使用[4]。

胶合木-混凝土连续组合梁是将胶合木和混凝土翼板通过抗剪连接件连接在一起共同工作的结构。组合结构充分发挥了胶合木顺纹抗拉强度高[5]和混凝土抗压性能较强的优势，达到结构最佳受力状态。由于胶合木-混凝土组合结构应用的增加，且能带来较好的经济和社会效益，近些年国内外学者对胶合木-混凝土组合梁进行了较为系统的研究。Lukaszewka等[6]研究了7 种剪力连接件，包括受拉螺钉、槽口螺钉、销钉等，并对螺钉或金属板连接的组合梁进行四点弯曲试验；组合梁的实测挠度和相对滑移与单轴有限元模型模拟组合梁的非线性分析结果有很好的对应关系。胡夏闽等[7]以1 根完全剪力连接、3 根部分剪力连接的组合梁为研究对象，进行梁的受弯试验，重点研究木-混凝土组合梁的变形发展过程和破坏形态，并分析连接件的布置方式和连接度对组合梁抗弯承载力以及刚度的影响。江雨辰和胡夏闽[8]通过木-混凝土组合梁螺栓抗剪试验，研究混凝土种类及螺栓直径对连接件受力性能的影响，结果表明，混凝土种类对连接件性能影响不大，增大螺栓直径可有效提高连接件的抗剪刚度和承载力。但无论是单一结构还是组合结构，简支梁和连续梁的受力性能都有所区别，目前对于胶合木-混凝土连续组合梁受力性能的相关研究较少。

鉴于此，本文通过控制胶合木-混凝土连续组合梁中抗剪连接件总数量不变的情况下改变其布置方式，运用ANSYS软件建立有限元模型，对比在均布荷载和对称集中荷载下几组模型的界面滑移、挠度和剪力的有限元计算结果，并分析其变化的趋势和原因，得出相对较为合理的抗剪连接件布置方式，以控制胶合木-混凝土连续组合梁的界面滑移和挠度，提高其结构的整体刚度及承载力，为实际工程中构件设计和相关研究提供参考。

1 有限元分析模型

1.1 胶合木-连续组合梁计算模型

胶合木-连续组合梁主要由2 部分组成，上层为混凝土翼板，下层为胶合木梁，中间通过抗剪连接件将二者连接在一起。如图1（a）所示，本文设计的胶合木-混凝土连续组合梁共布置两跨，且左右两边等跨长度均为6 m，全跨度长为12 m。参考GB/T 50708—2012《胶合木结构技术规范》要求，本文确定胶合木梁高为400 mm、梁宽为200 mm；考虑胶合木-混凝土连续组合梁的强度、刚度以及其最小截面尺寸要求，根据JGJ 138—2016《组合结构设计规范》确定混凝土翼板的板厚为100 mm、板宽为800 mm。胶合木-混凝土连续组合梁截面尺寸如图1（b）所示。

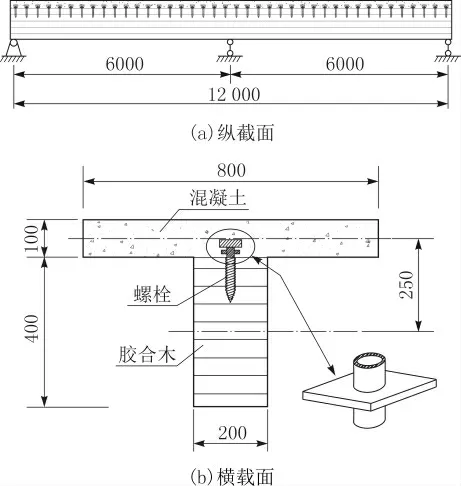
图1 胶合木-混凝土连续组合梁截面示意

有限元模型分别取均布荷载q=20 kN/m 和对称集中荷载P=120 kN 作用下进行分析计算，2 种荷载的形式不同，但荷载总量相同。胶合木-混凝土连续组合梁荷载作用下的计算简图如图2 所示。

图2 胶合木-混凝土连续组合梁计算简图

1.2 材料属性

（1）混凝土。有限元建模采用强度等级为C30 的混凝土，其轴心抗压强度设计值fc=14.3 MPa、弹性模量Ec=30.0 GPa、泊松比μc=0.2、容重γc=25 kN/m3。

（2）胶合木。胶合木是各向异性材料，在互相垂直的2 个方向上具有不同的性能指标，这一特性对其破坏特征有着显著的影响，所以在进行有限元建模时，胶合木3 个相互垂直方向的参数是不可忽略的重要指标。如图3 所示，3 根主轴分别代表胶合木纵向（L）、径向（R）、切向（T）的弹性主方向，而且3个方向分别对应ANSYS 有限元软件建立模型中坐标轴x、y、z的方向；参考杨海旭等[9]的研究，选用花旗松为树种的胶合木，其弹性阶段的各项参数如表1 所示。其中Ex、Ey和Ez分别代表胶合木纵向、径向和切向（x、y、z三个方向）的弹性模量；Gxy、Gxz和Gyz分别代表胶合木L-R平面、L-T平面和R-T平面（x-y、x-z、y-z三个平面）内的剪切模量。

表1 胶合木弹性阶段各项参数MPa

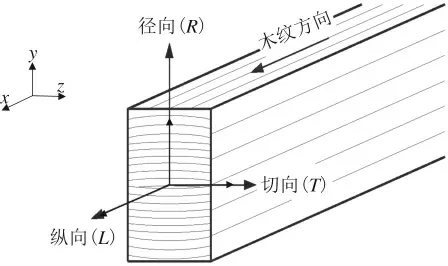
图3 胶合木正交三向主轴

（3）抗剪连接件。参考Lukaszewka 等[6]的研究，采用SST+S 类型的剪力连接件，由尺寸为φ20 mm×120 mm 的六角头螺栓和尺寸为φ20 mm×47 mm 的开洞钢板组合而成；由式（1）确定胶合木-混凝土组合梁中抗剪连接件的荷载P-滑移S曲线，如图4 所示，取抗剪连接件正常使用状态下的刚度，k=5.9 kN/mm。

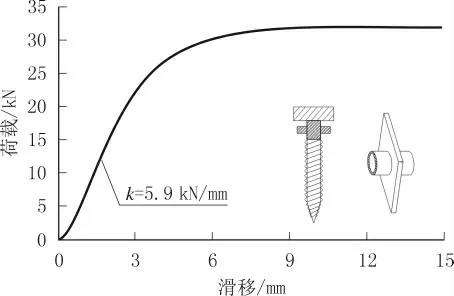
图4 荷载-滑移曲线

1.3 单元类型

运用有限元软件ANSYS 建立胶合木-混凝土连续组合梁模型。混凝土板采用Solid65 实体单元模拟，由于本文中所有数值模拟均考虑混凝土为线弹性材料，故不考虑混凝土的压碎和开裂。由于胶合木为正交各向异性材料，故采用Solid45实体单元对其进行模拟，该单元能很好地反映正交各向异性材料的受力情况。连接件是表现混凝土板和胶合木梁之间滑移效应以及受力性能的关键所在，因此采用Combine39 弹簧单元模拟2 种材料之间的螺栓较为合适。有限元单元模型如图5 所示。

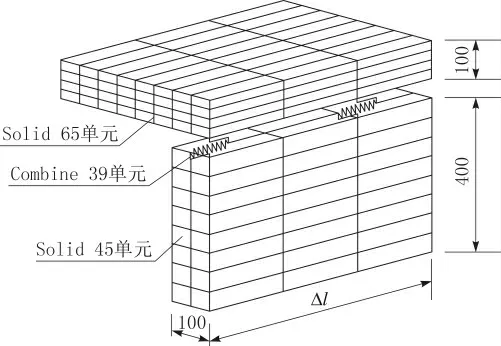
图5 有限元单元模型示意

1.4 有限元模型的计算验证

取1.1 中设计的均布荷载下连续组合梁的1/2（即长6 m的简支梁）进行计算，截面形式以及单元类型均保持不变，螺栓间距e=200 mm。参考文献[4，10]对组合梁有效刚度的研究进行分析，简支组合梁截面有效刚度按式（2）计算：

式中：E——材料的弹性模量，MPa；

I——截面惯性矩，mm4；

A——截面面积，mm2；

a——截面形心到组合梁截面中和轴的距离，mm；

Seff——抗剪连接件的等效间距，mm；

K——抗剪连接件的刚度，kN/mm；

L——简支组合梁的跨度，mm；

各参数下标的c和g——分别代表混凝土和胶合木。

对简支组合梁在均布荷载作用下的挠度按照式（3）进行验算：

其中，简支组合梁在均布荷载作用下的弯矩方程为M（x）为均布荷载（kN/mm）。代入对应的参数计算可得简支组合梁挠度的解析解。胶合木-混凝土简支组合梁挠度解析解和数值解的对比曲线如图6 所示。

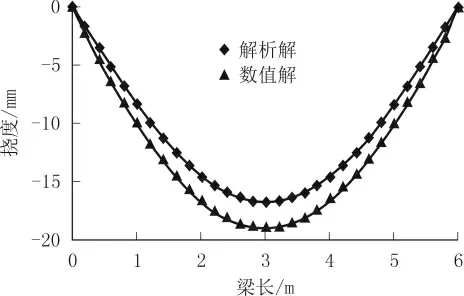
图6 胶合木-混凝土简支组合梁挠度解析解与数值解对比明有限元模型选择较合适、建模精度较好，可进一步用于胶合木-混凝土连续组合梁的有限元计算分析。

由图6 可见，2 条曲线均呈抛物线分布，跨中挠度最大、沿梁的两端挠度越来越小且左右对称。挠度解析解和数值解虽不能较好地吻合，但是两者也比较接近，跨中的解析解和数值解分别为16.80、19.12 mm，相差约为12%，有限元单元的选择会影响最终的结果，该值在工程中属于可接受的范围，故表

2 有限元计算结果分析

为了方便对抗剪连接件布置方式的影响效果进行对比分析，参考王鹏等[11]对钢-混凝土组合梁中抗剪连接件分段布置时滑移的研究分析，本文保持胶合木-混凝土连续组合梁的材料属性、跨度、截面形式及建模使用的单元均不变的前提下，改变抗剪连接件分布的位置并控制其总数量不变。

共设计4 组试件进行建模计算，具体分布情况如表2 和图7 所示，胶合木-混凝土连续组合梁有限元建模如图8 所示。

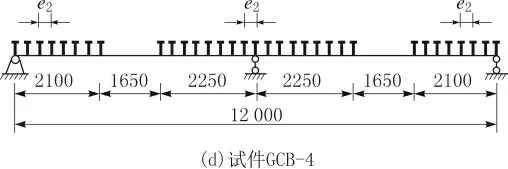
图7 各试件抗剪连接件分布示意

图8 胶合木-混凝土连续组合梁模型

组合梁虽然用抗剪连接件将胶合木和混凝土连接成整体，但实际工程中不可能大量使用连接件使组合梁达到完全剪切的效果。部分剪切连接胶合木和混凝土的交界面有剪力存在，因而会产生界面滑移[12]。即使组合梁完全剪切连接，当抗剪连接件受剪产生变形后依然会出现界面滑移。界面滑移的存在，会使组合梁的挠度增大、强度降低、曲率变大、抗弯刚度变小[13]。为确定一种较为合适的抗剪连接件布置方式，对2种不同荷载工况下4 组试件的界面滑移、挠度和梁中剪力分布情况进行分析。

2.1 界面滑移分析

2 种荷载工况下试件滑移的有限元计算结果如图9 和表3 所示。

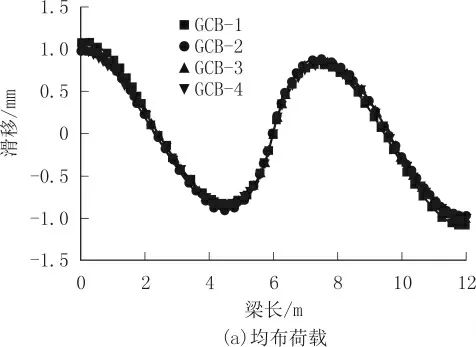
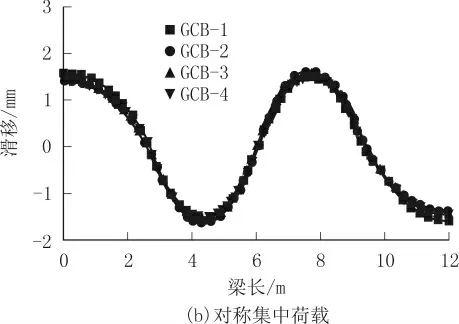
图9 不同荷载工况下界面滑移对比

表3 不同荷载工况下组合梁梁端的滑移

由图9 可见，连续组合梁在2 种不同荷载工况下的界面滑移大小均受到抗剪连接件布置方式的影响，但不管哪种布置方式下，其中间支座处的滑移均为0。分段布置抗剪连接件的试件GCB-2、GCB-3 和GCB-4 产生的界面滑移比均匀布置抗剪连接件的试件GCB-1 要小。

由表3 可见，在同等刚度下，对称集中荷载作用下的滑移要比均布荷载作用下的滑移大。GCB-1 梁端界面滑移最大，而分段布置抗剪连接件的组合梁在均布荷载作用时和对称集中荷载作用时梁端界面滑移最小的都是试件GCB-4，表明抗剪连接件分段布置的梁端界面滑移要比全梁上均匀布置的梁端界面滑移小。均布荷载作用下，3 种分段布置方式的梁端界面滑移较均匀布置的试件GCB-1 减小了9.89%~11.76%；对称集中荷载作用下，较试件GCB-1 减小了9.8%~12.09%。2种工况下降幅相近。

综上可以看出，抗剪连接件的布置方式对界面滑移的影响较大。本文为了保持抗剪连接件总的数量一致，在设置抗剪连接件间距时相对保守，若适当增加分段布置的间距，界面滑移的减小幅度可能更为明显。图9 和表3 的计算结果都可以明显看出，试件GCB-4 的抗剪连接件布置方式较另外几组的布置方式更合适。

2.2 挠度分析

抗剪连接件的抗滑移刚度会影响胶合木-混凝土连续组合梁整体的刚度，其布置方式的不同也会导致连续组合梁的刚度发生变化，所以其挠度也会受到影响。4 组试件在不同荷载工况下的有限元计算挠度结果如图10 和表4 所示。

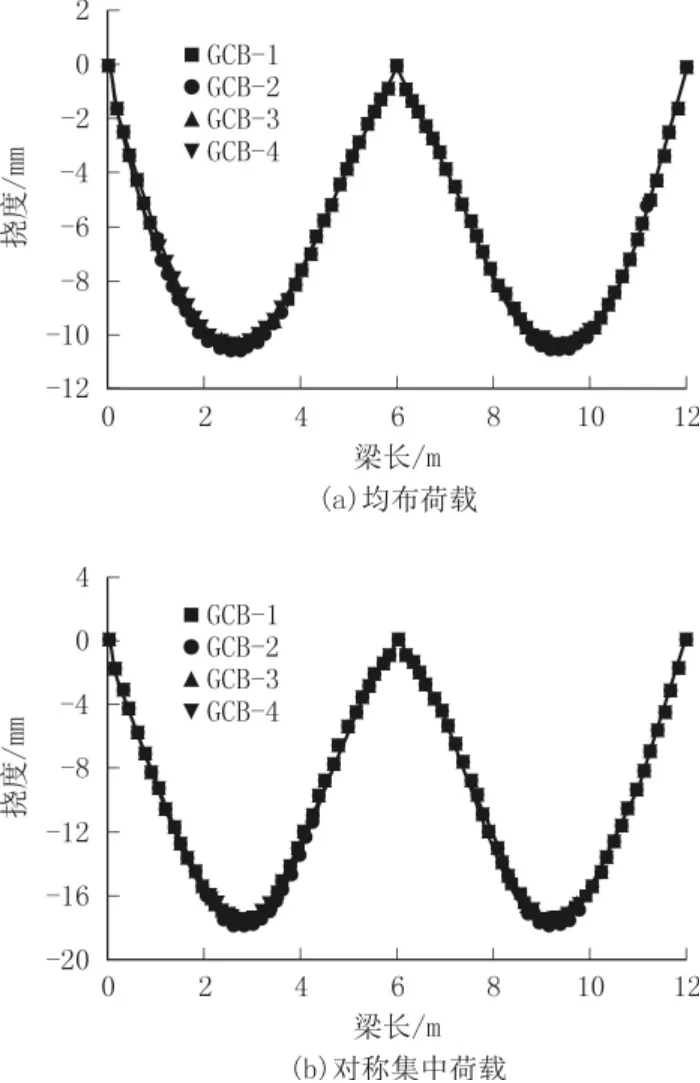
图10 不同荷载工况下挠度对比

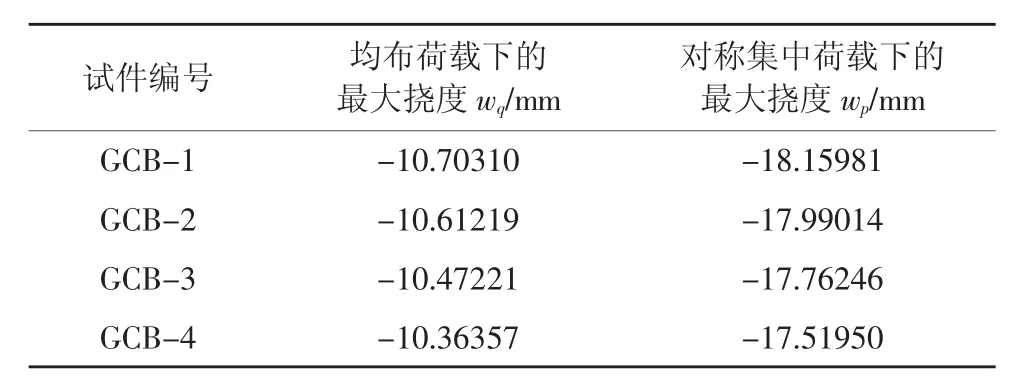
表4 不同荷载工况组合梁的最大挠度

由图10 可见，挠度为0 点处于组合梁的两端和跨中支座处，而挠度最大点出现在（5/24-1/4）L区域，L为连续组合梁的全梁跨度。

由表4 可见，无论是在均布荷载还是对称集中荷载下，抗剪连接件均匀布置的试件GCB-1 比分段布置的另外几组试件挠度大，其中试件GCB-4 的挠度最小。由于施加的力较小，除挠度最大值的区域，其他部分挠度基本重合，若适当加大荷载，挠度变化趋势会更明显。

2.3 剪力分析

综合2.1 和2.2 的分析可知，试件GCB-4 产生的界面滑移和挠度在4 组试件中均最小。相对其他位置，4 组试件中距离梁两端约为（1/6-1/4）L的区域滑移均较小，所以该区域在实际工程中可不用布置抗剪连接件，其余位置均匀布置即可。

剪力连接件在部分剪切连接组合梁中传递混凝土和胶合木交界面上的水平剪力，从而引起交界面上出现滑移，使得组合梁截面曲率和挠度增大。为研究连续组合梁中剪力的分布，对混凝土翼板和胶合木梁各自承担的剪力进行分析。由于连续组合梁左右两跨抗剪连接件的布置方式均对称且荷载工况相同，故有限元软件中提取的剪力从跨中沿梁端呈反对称形式，取左边半跨（0~6 m）的剪力数据进行分析。本节对抗剪连接件布置最为合适的试件GCB-4 中剪力分布情况进行分析，结果如图11 所示。

图11 不同荷载工况下试件GCB-4 的剪力分布

由图11 可见，荷载总量不变的情况下，无论是承受均布荷载还是对称集中荷载，组合梁交界面大部分的剪力由胶合木梁承担。除此之外，均布荷载作用下2 种材料在支座附近承担的剪力较大，跨中支座处胶合木梁承担的剪力最大，约为该截面混凝土翼板承担剪力的9 倍；对称集中荷载作用下混凝土翼板在集中力位置处承担的剪力最大，约为均布荷载作用下该位置剪力的25 倍，胶合木梁在跨中支座处承担的剪力最大，同样约为该截面混凝土翼板承担剪力的9 倍。综上，均布荷载作用和集中荷载作用时应分别在支座附近和集中力作用处的混凝土翼板内添加足够的横向钢筋，避免混凝土翼板过早出现开裂现象。

3 结 论

抗剪连接件是保证混凝土翼板和胶合木梁共同工作的前提，因此针对部分剪切连接胶合木-混凝土连续组合梁中抗剪连接件的分布方式进行研究分析。通过有限元数值模拟值的对比，分析了4 组不同试件不同荷载工况下的界面滑移、挠度以及均匀布置抗剪连接件试件的剪力，主要结论如下：

（1）在荷载总量相同且抗剪连接件布置方式相同的情况下，2 种荷载工况中对称集中荷载下连续组合梁的界面滑移和挠度最大。

（2）分段并变换抗剪连接件的布置间距可以减少连续组合梁所产生的界面滑移和挠度。

（3）试件GCB-4 中先分段再减小抗剪连接件间距并按此间距在分段部分均匀布置的方式最合适，该试件端部界面滑移以及中间支座附近两侧的界面滑移均最小。

（4）试件GCB-4 布置抗剪连接件的方式在进行施工时比较便捷，只需计算出距离梁两端（1/6-1/4）L的区域（L为连续组合梁两跨的长度），该区域不用布置，其他部分按照适当的间距等距进行布置即可。

（5）连续组合梁中胶合木承担的剪力较大，对称集中荷载下集中力位置截面处混凝土翼板的剪力最大，可能会导致该截面附近的混凝土过早开裂，因此在实际工程中应在组合梁的这些位置配置适量的箍筋。