纵向数据下部分线性模型的估计与应用

盛利利,亢芳圆

(北京信息科技大学 理学院,北京 100192)

0 引言

纵向数据应用广泛,常见于医学、经济学、金融学等领域。在许多学科,如经济学中,纵向数据又叫做面板数据。在纵向数据中,同一个体的不同观测点的数据是相关的,而来自不同个体之间的观测是独立的。因此,在估计这类数据时,考虑具有相关性的回归方法非常有必要。

针对纵向数据的特点,许多统计学者用参数模型进行了研究,如Nelder等[1]提出广义线性模型,Liang等[2]提出广义估计方程 (generalized estimating equation,GEE) 方法。参数回归模型的估计理论目前已相对成熟,但是模型只考虑参数部分,在处理实际的问题时,适应性和解释能力不足,所以在模型中加入非线性部分是一种增强模型适应性的可行方法。如Engle等[3]提出的部分线性模型,该模型结合了参数模型和非参模型的优点,受到了不同领域学者的广泛关注。

对于纵向数据下的部分线性模型,Zeger等[4]首次进行研究,并将其应用于HIV阳转者CD4细胞数量的时间演变数据。Lind等[5]使用 profile 核估计法估计兴趣参数。He等[6]对非参部分进行了B 样条估计,提出了M估计法。Huang等[7]利用样条逼近和GEE对其参数部分和非参数部分进行估计。薛留根等[8]利用经验似然方法构造了参数分量与非参数分量的置信区间。Bai等[9]将二次推断函数 (quadratic inference function,QIF) 方法应用到纵向数据部分线性模型的统计推断。文献[4-9]的研究都涉及工作协方差矩阵的求解,但是真实的工作协方差矩阵是未知的,这就需要额外的方法来估计它。

为了简化估计中需要的参数和工作协方差矩阵结构,Yao等[10]提出了一种在纵向数据背景下,基于Cholesky分解和profile最小二乘法技术估计非参数模型的方法,该方法避免了估计工作协方差矩阵,并且证明了所提出的估计是渐进有效的,就如真实工作协方差矩阵是先验已知的一样;随后牟婷[11]将该方法推广至纵向数据下的部分线性模型,同Yao等[10]提出的估计过程一样运用了Cholesky分解和profile最小二乘法技术,使用局部多项式估计方法处理非参数部分。田瑞琴等[12]基于Cholesky分解,提出了一种纵向数据下的半参数联合均值协方差模型贝叶斯估计,运用B样条来逼近非参数部分。文献[10-12]巧妙利用Cholesky分解技术处理纵向数据具有的组内相关性,避免了估计工作协方差矩阵结构,但是大都采用样条函数处理非参部分并结合较复杂的迭代算法,才能得到兴趣参数的估计值。

为了解决这个问题,可将最小二乘核估计方法应用于部分线性模型的估计中,可以不进行迭代算法,得到兴趣参数的显示解,计算简便。如最早由Denby[13]提出的独立数据下的部分线性模型的最小二乘核估计方法,运用了核估计来处理非参数部分,将非参数部分线性近似表示,最后运用最小二乘方法估计兴趣参数。田萍等[14]将最小二乘核估计方法运用到纵向数据部分线性模型中,提出了广义的最小二乘核估计方法。

本文结合最小二乘核估计方法和Cholesky分解技术,提出一种纵向数据下部分线性模型的估计方法,用最小二乘核估计处理参数和非参数部分的估计,用Cholesky分解处理纵向数据组内相关性,得到兴趣参数的显式解。数值模拟表明本文方法在估计参数部分和非参数部分具有良好的估计性质,并将其应用于空气质量数据,表明估计方法在实际应用也有较好的可行性。

1 模型的提出及估计

假设有n个观测个体,对每个个体有J次观测,则有观测值(Xij,Yij,Tij)(i=1,2,…,n;j=1,2,…,J)。其中Xij、Yij为第i个个体在时间为Tij时的协变量和因变量,一类重要的部分线性模型有如下形式:

Yij=βTXij+g(Tij)+εij

(1)

式中:β=(β1,β2,…,βp)T;Tij为一维协变量;g(·)为未知平滑函数;εij为随机误差。记第i个个体的误差向量为εi=(εi1,εi2,…,εiJ)T,{εi}相互独立,均值和方差分别满足E(εi)≈0,Var(εi)=C。

为了处理模型(1)中个体内部的随机误差协方差矩阵C难以求解的问题,使用Yao等[10]提出的方法,用Cholesky分解将随机误差的协方差矩阵C转变为对角矩阵,进而不再估计协方差矩阵C。这里假设cov(εi|Xi,Ti)=C,存在一个对角线元素均为1的下三角矩阵Φ,满足

cov(Φεi)=Φcov(εi)ΦT=D

(2)

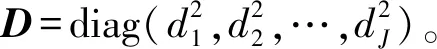
εi1=ei1

εij=Φj,1εi,1+Φj,2εi,2+…+Φj,j-1εi,j-1+eij

i=1,2,…,n;j=2,3,…,J

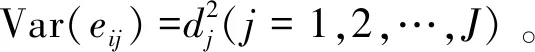
假设{ε1,ε2,…,εn}已知,得到带有不相关误差eij的部分线性模型:

Yi1=g(Ti1)+βTXi1+ei1

Yij=g(Tij)+βTXij+Φj,1εi,1+Φj,2εi,2+…+

Φj,j-1εi,j-1+eij

i=1,2,…,n;j=2,3,…,J

(3)

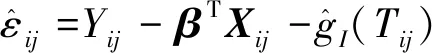
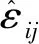
Yi1=g(Ti1)+βTXi1+ei1

i=1,2,…,n;j=2,3,…,J

令

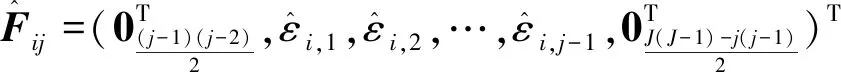
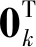
(4)

式中:

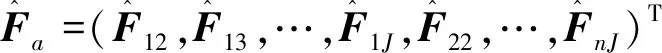
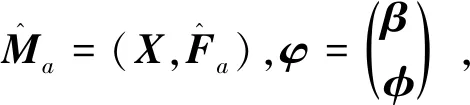
(5)

至此,通过Cholesky分解技术已将具有组内相关性的模型(1)转变为具有组内独立性的模型(5)。

为了得到模型(5)中未知的G(T)和φ,利用最小二乘核估计方法估计模型(5)的参数和非参数部分。

假设φ已知,令

式中:K(·)为核函数;h为窗宽。

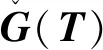
其中

有

(6)

则估计的误差方程为

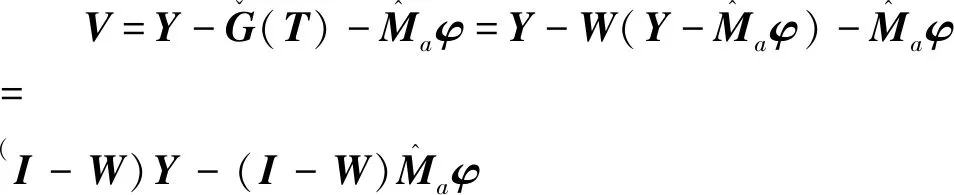
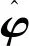
H-1(I-W)Y

(7)

其中

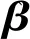
(8)

(9)

2 数值模拟

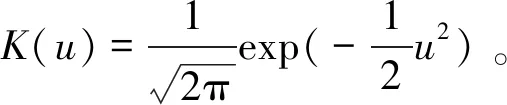
表1 不同回归函数下的参数估计Table 1 estimators under different regression functions

为了体现平滑函数g(t)拟合的优良特性,在平滑函数g(t)分别为cos(2πt)、e-4t和个体数为30时,将g(t)估计曲线和真实曲线作比较,见图1。

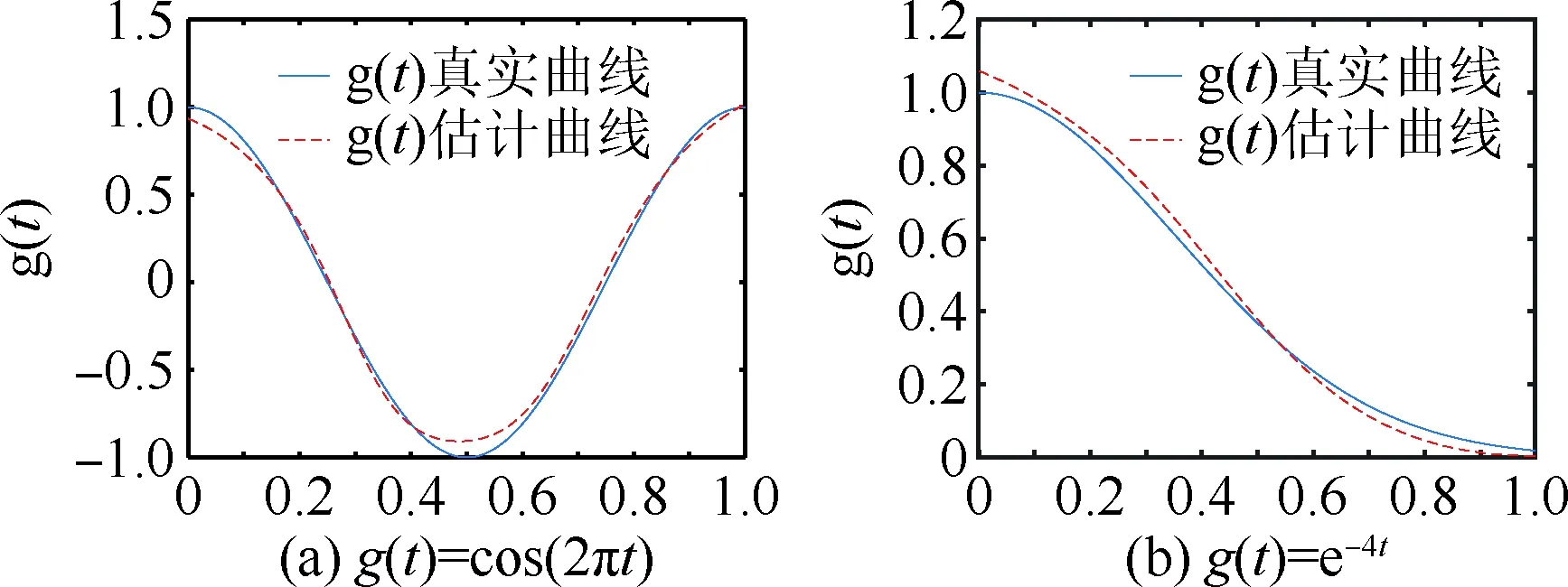
图1 g(t)的真实曲线和估计曲线Fig.1 The real curve and estimated curve of g(t)

从图1可以看出,真实曲线与估计曲线基本重合,拟合有很好的效果。

综上,本文的估计方法在有限样本模拟中有较好的表现,说明本文的估计方法是可行的。

3 空气质量数据的应用

本节将本文提出的方法应用到来自 “空气质量在线监测分析平台”的空气质量数据,数据选取北京2014年1月到2021年12月的空气质量数据,数据包含:PM2.5质量浓度、PM10质量浓度、NO2质量浓度、CO质量浓度、SO2质量浓度、O3质量浓度的月平均数据。数据来源链接为:https://www.aqistudy.cn/historydata/。

通常一个地区的PM2.5的形成与当地一段时间内的PM10质量浓度、NO2质量浓度、CO质量浓度、SO2质量浓度、O3质量浓度有关。在应用中,将PM2.5质量浓度作为模型(1)中的响应变量Y,将其余气体的质量浓度作为模型(1)中的协变量X或T。为了确定参数部分的协变量X和非参数的协变量T,分别作PM2.5质量浓度与PM10质量浓度、NO2质量浓度、CO质量浓度、SO2质量浓度、O3质量浓度的散点图,如图2～6所示。

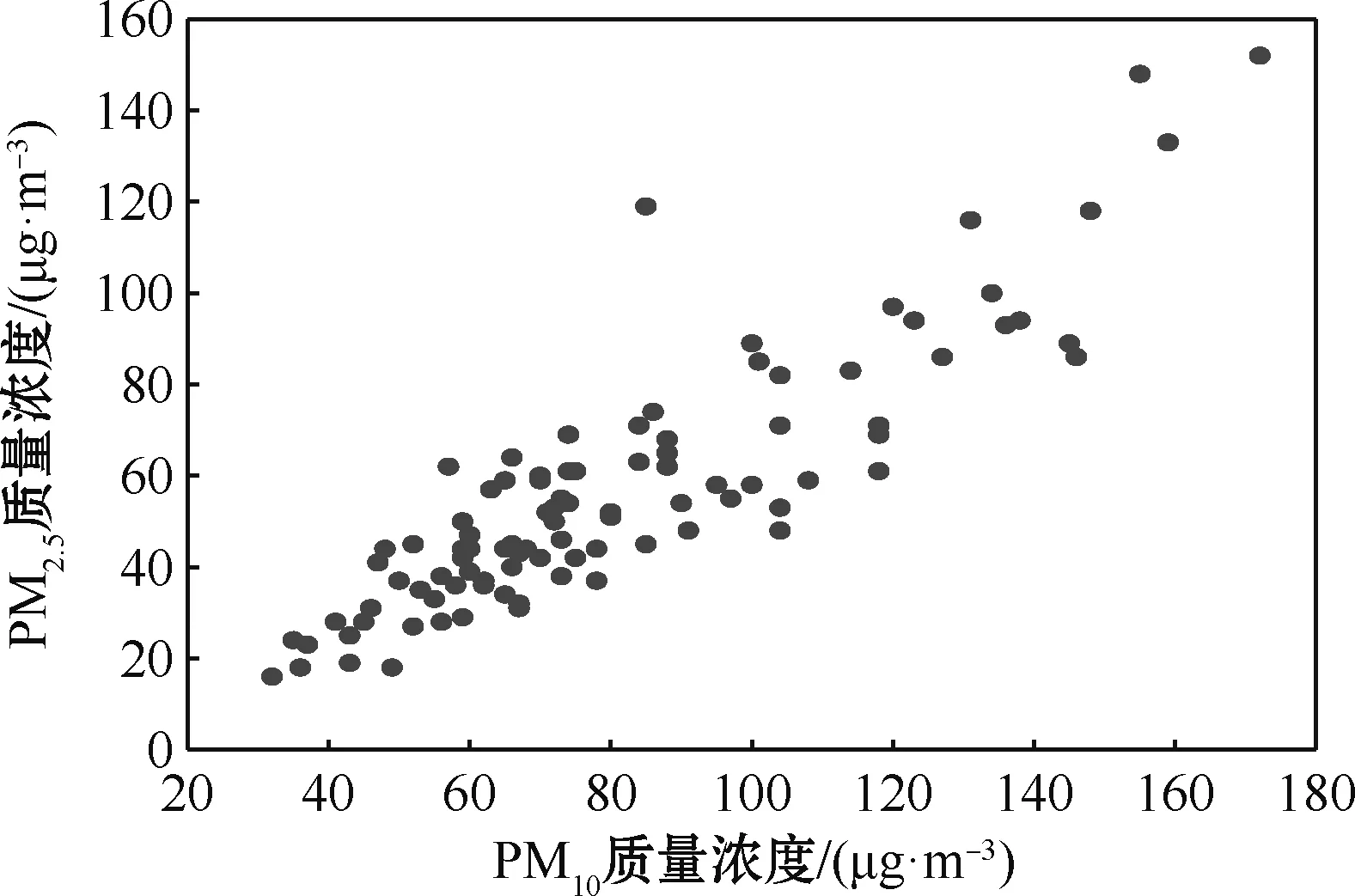
图2 PM2.5与PM10质量浓度散点图Fig.2 Scatter plot of mass concentration of PM2.5 and PM10

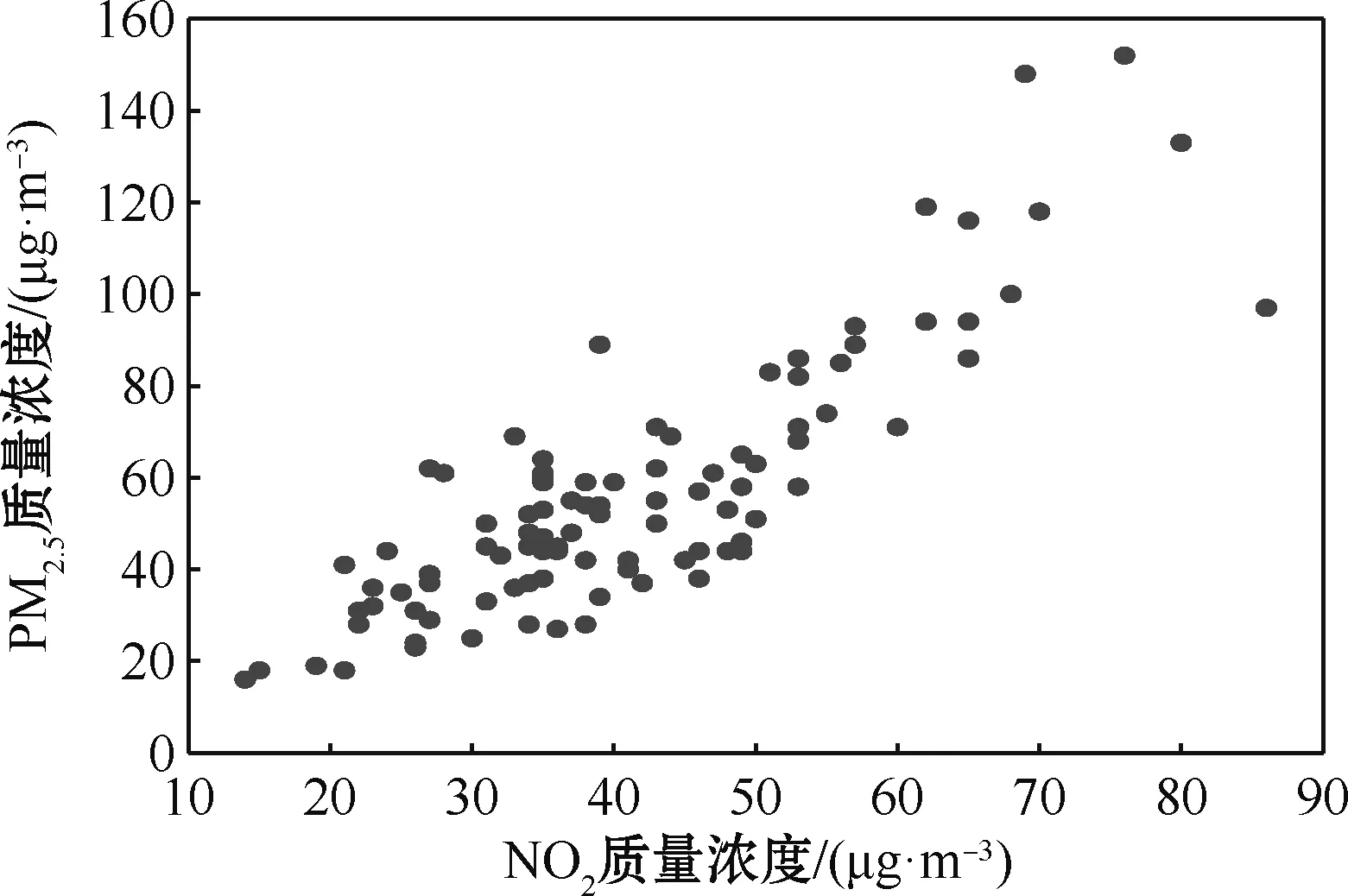
图3 PM2.5与NO2质量浓度散点图Fig.3 Scatter plot of mass concentration of PM2.5 and NO2

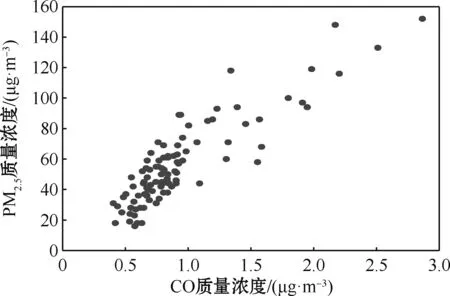
图4 PM2.5与CO质量浓度散点图Fig.4 Scatter plot of mass concentration of PM2.5 and CO

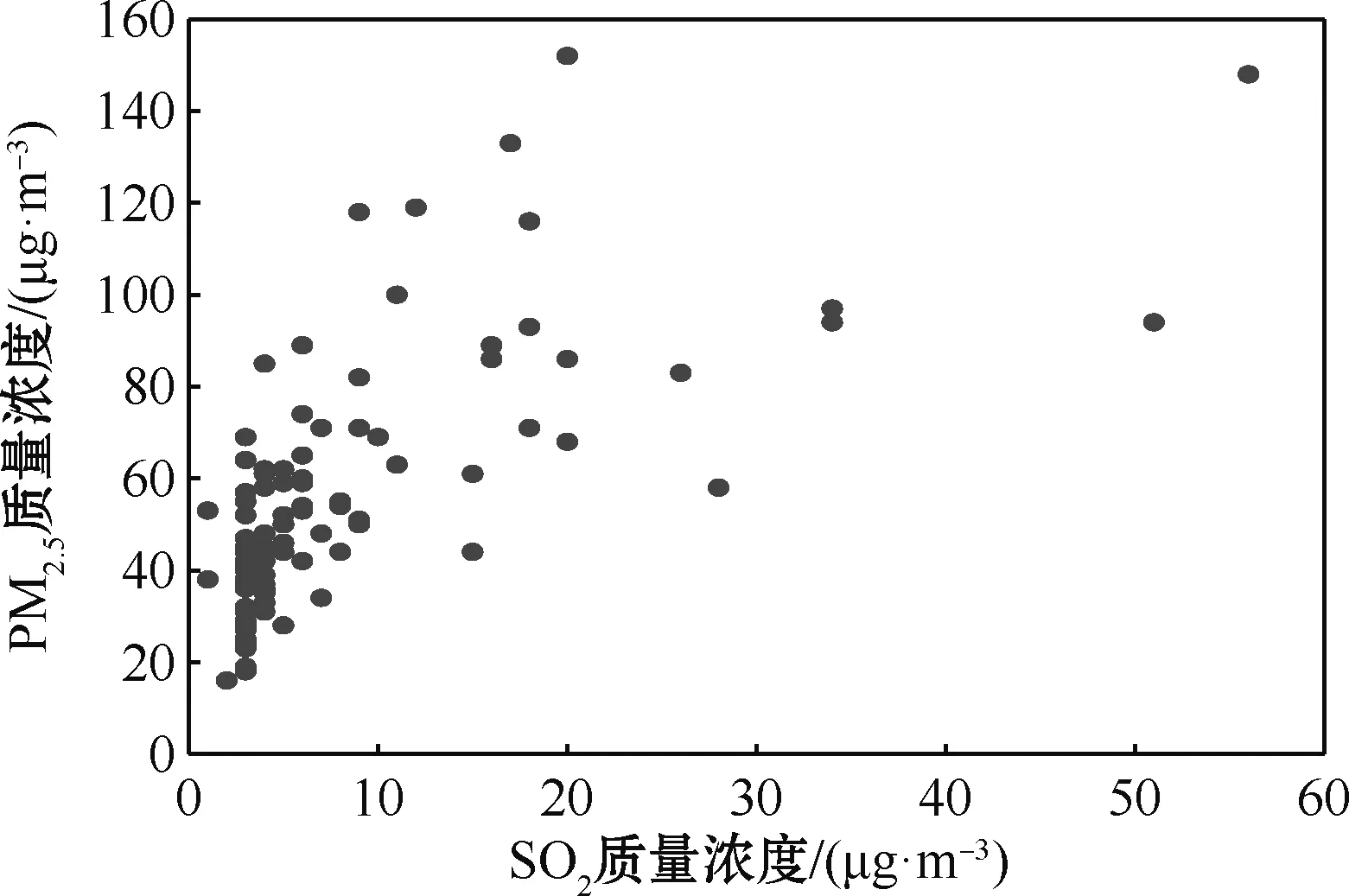
图5 PM2.5与SO2质量浓度散点图Fig.5 Scatter plot of mass concentration of PM2.5 and SO2

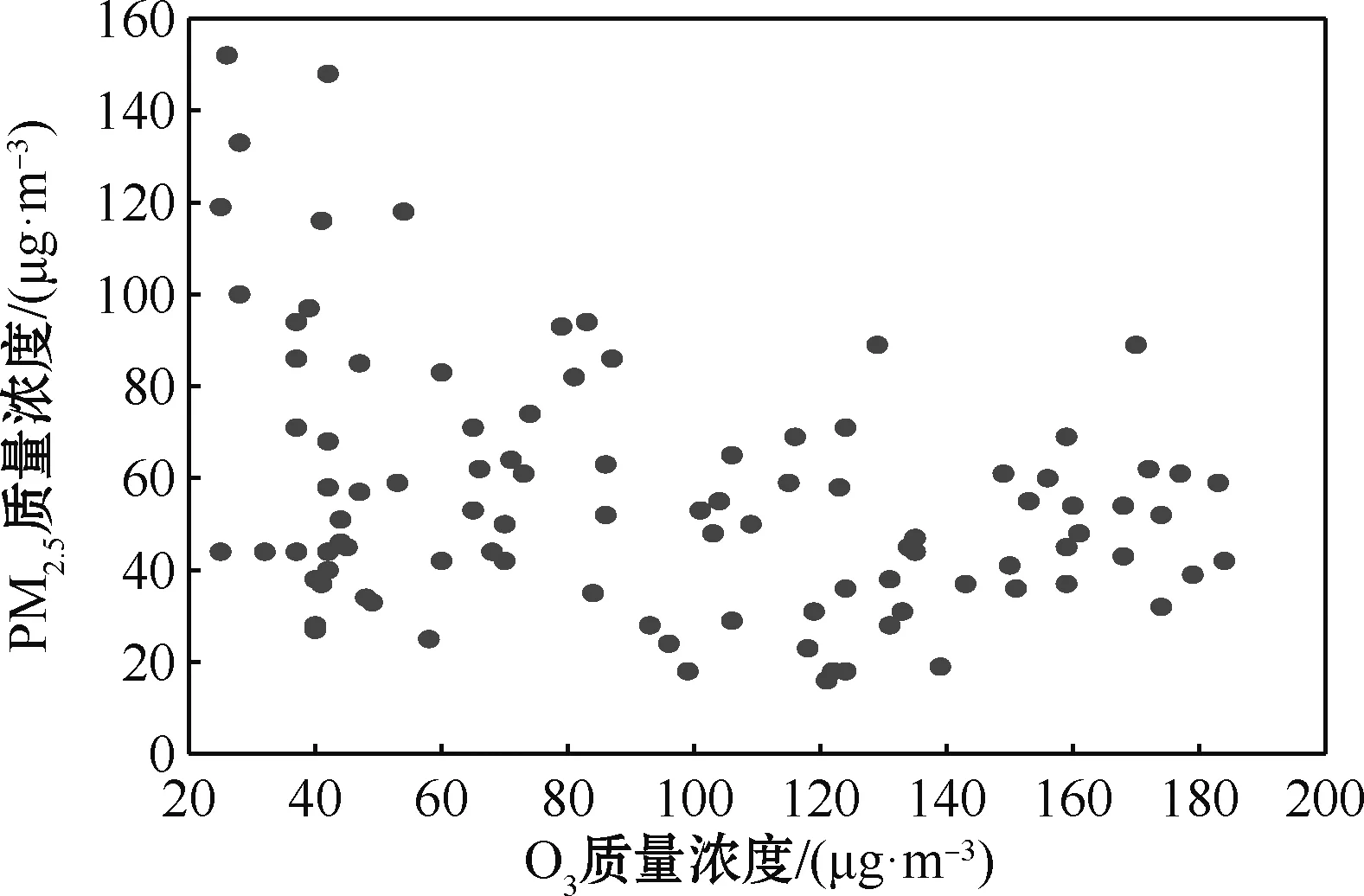
图6 PM2.5与O3质量浓度散点图Fig.6 Scatter plot of mass concentration of PM2.5 and O3

观察图2～6发现,PM2.5质量浓度分别与PM10质量浓度、NO2质量浓度、CO质量浓度、SO2质量浓度有明显的线性关系,而与O3质量浓度没有明显的线性关系。因此,将PM10质量浓度、NO2质量浓度、CO质量浓度、SO2质量浓度作为参数部分的协变量,O3质量浓度作为非参数部分的协变量。

将北京每一年的每一个月的空气质量数据作为一个观测点,假定每年中月与月之间具有相关性,年与年之间相互独立,适用于本文提出的纵向数据估计方法。

为了体现本文方法与其它常用方法的实际应用差异,将本文方法、半参数回归(不考虑组内相关性的部分线性模型方法)、参数回归(不考虑组内相关性的线性模型方法),分别应用到北京市空气质量数据中,得到三种模型关于真实PM2.5估计的折线如图7所示,同时计算每种方法的PM2.5估计值与真实值之间的均方误差,见表2。

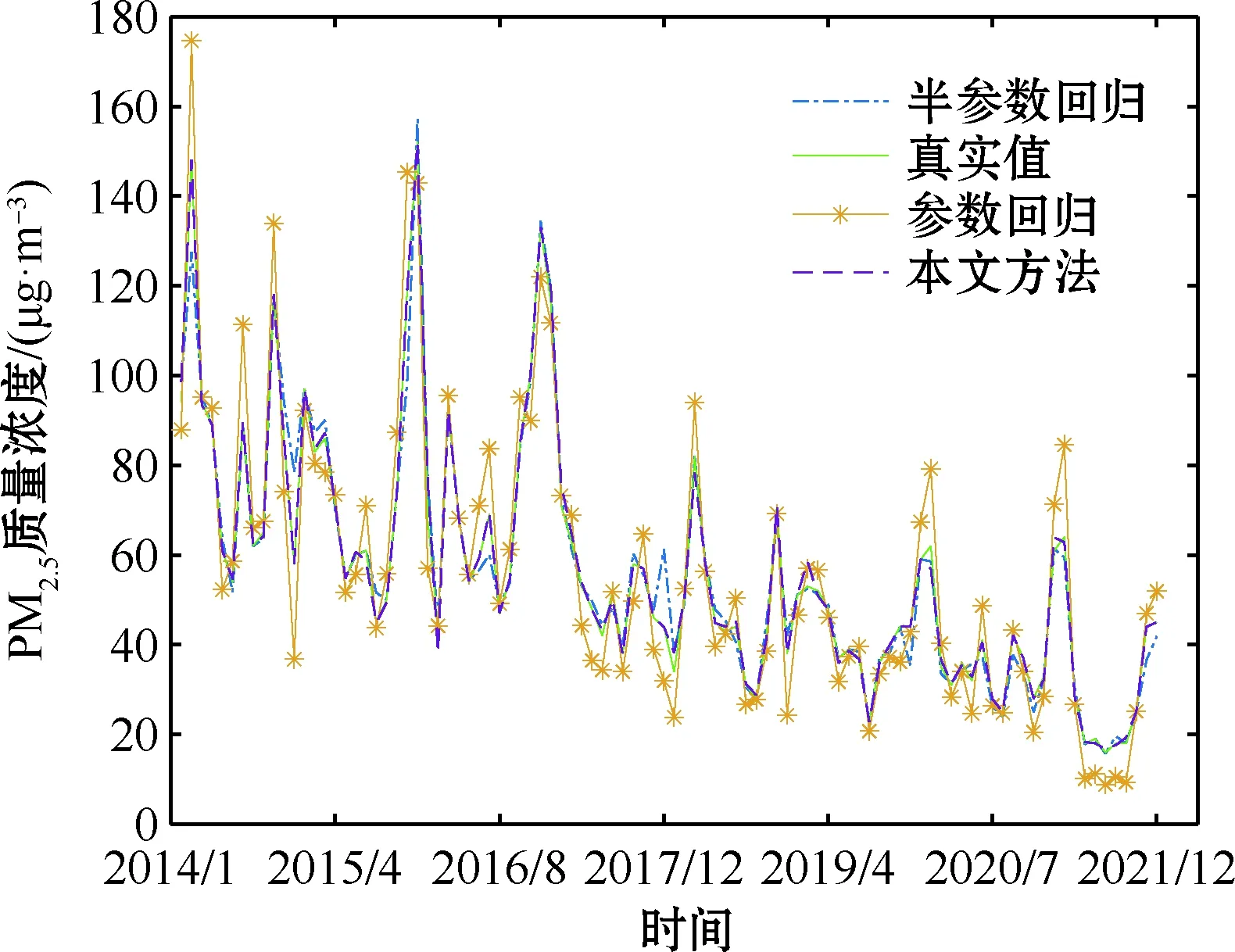
图7 真实数据与三种估计的折线图Fig.7 Real data and three estimated line charts

表2 不同回归方法关于PM2.5估计值与真实值的均方误差Table 2 The mean square error of PM2.5 estimated value and real value by different regression methods

从图7可看出,本文方法和半参数回归方法拟合的折线与真实PM2.5折线无明显差异,而参数方法拟合的折线与真实PM2.5折线差异较大,说明参数模型不适用拟合本节的空气质量数据。

从表2可看出,本文方法均方误差最小,说明如果忽略数据每一年中月与月之间的相关性,会对拟合有较大的影响,简单地考虑数据之间的关系对拟合的效果有很大的折损。本文方法回归拟合中参数部分的协变量系数分别为0.143,0.538,28.571,0.206,说明PM10质量浓度、NO2质量浓度、CO质量浓度、SO2质量浓度这四种因素都影响着PM2.5的形成。

综上可得,PM2.5的产生与PM10质量浓度、NO2质量浓度、CO质量浓度、SO2质量浓度有密切的关系;北京市空气质量数据中,PM2.5的数值逐年下降,北京的空气环境治理有明显的成效。将空气质量数据作为纵向数据并使用本文提出的估计方法,能够得到较好的拟合效果。

4 结束语

本文将Cholesky 分解和最小二乘核估计方法相结合,给出了新估计方法的具体估计过程,用Cholesky 分解来处理纵向数据的组内相关性,用最小二乘核估计来处理部分线性模型中的非参数部分,由于可以得到显式解,所以该估计方法可以较为迅速地得出估计结果,比一般的迭代方法有明显的优势,并且不再对纵向数据中的工作协方差矩阵进行估计,简化的估计程序又节约了计算成本。通过数据模拟说明该估计方法的可靠性。本文将估计方法运用于空气质量数据的分析中,结果表明该估计方法适用于常见数据的应用分析。这也为分析其它类型的纵向数据提供了解决思路。