调频多普勒引信EMD数字包络检波算法

熊文俊,马 捷,李维山

(西安机电信息技术研究所,陕西 西安 710065)

0 引言

调频多普勒(frequency modulation Doppler,FMD)引信[1]凭借对回波信号与发射信号频率差包含的距离信息进行分析来实现定距功能,具有体积小、成本低、精度高、抗干扰能力强等特点,近年来被广泛使用。考虑到传统FMD引信系统中使用模拟电路进行检波容易受到工艺、环境等因素影响,为了提高FMD引信系统的可靠性,可以利用数字检波算法来代替模拟电路检波。

常用的数字检波方法有Hilbert检波[2-3],同步检波[4],正交检波[5-6]。Hilbert检波通过对待检波信号做Hilbert变换,得到具备90°相移的输出信号,对两者平方求和得到包络信号。同步检波用与待检波信号同频同相的参考信号与之相乘,然后利用低通滤波滤除高频分量得到包络信号。正交检波将待检波信号分为两路,分别与相位相差90°的参考信号相乘,利用低通滤波滤除高频分量,对两路输出信号平方求和得到包络信号。

上述数字检波方法适用于受到幅度调制的单频正弦波,而在调频多普勒引信系统中的谐波信号表达式[7]较为复杂,无法使用上述数字检波方法进行检波。本文针对此问题,提出一种基于EMD[8-10],利用极值点与最小二乘曲线拟合来实现包络检波的算法。该算法对于待检波信号表达式没有严格要求,对表达式较为复杂的FMD引信系统谐波信号可以正常实现检波功能。

1 FMD引信系统谐波信号特征分析

1.1 谐波信号特征分析

FMD引信系统发射三角调频(triangular frequency modulation,TFM)连续波信号频率-时间曲线如图1所示。图中,纵轴为瞬时频率f(t),横轴为瞬时时间t;TFM连续波信号的调制频偏、调制周期分别用B、T表示;τ表示发射信号与回波信号之间的时延。由于信号在时间域上的平移对频域幅值不产生影响,只是引入与频率成线性关系的相移分量,为了便于后续分析,设置时间零点位置使差频信号关于时间零点对称。

图1 三角调频连续波信号时频曲线Fig.1 Time-frequency curve of triangular FM continuous signal

由图1可以看出,差频信号为周期变化的信号,周期为T。在一个周期[-T/2,T/2] 内,差频信号根据信号特征可以分为5个区间：[-T/2,-T/2+τ/2],[-T/2+τ/2,-τ/2],[-τ/2,τ/2],[τ/2,T/2-τ/2],[T/2-τ/2,T/2]。可以得到TFM连续波发射信号在区间[-T/2+τ/2,-τ/2]内瞬时频率与时间的对应关系为

(1)

式(1)中,fT表示调制频率,fT=1/T。TFM连续波发射信号在区间[τ/2,T/2-τ/2]内瞬时频率与时间的对应关系为

(2)

根据频率与相位的关系可以对相位进行求解,得到TFM连续波发射信号在区间[-T/2+τ/2,-τ/2]的对应相位：

(3)

TFM连续波发射信号在区间[τ/2,T/2-τ/2]的对应相位：

(4)

TFM连续波回波信号的相位与TFM连续波发射信号存在时延τ,以t-τ替换式(3)、式(4)中的t可以得到回波信号的相位表达式,根据发射信号与回波信号相位可以求出差频信号相位在区间[-T/2+τ/2,-τ/2]表达式：

φ1(t)=4πBfTτt+πBτ+2πfcτ。

(5)

差频信号相位在区间[τ/2,T/2-τ/2]表达式：

φ2(t)=-4πBfTτt+πBτ+2πfcτ。

(6)

由式(5)、式(6)可求出差频信号的完整表达式为

(7)

由于时延τ相对于差频信号周期T占比很小,因此只需要对区间[-T/2+τ/2,-τ/2],[τ/2,T/2-τ/2]内的差频信号进行分析即可。由式(7)可以看出差频信号在[-T,T]内为偶函数,对差频信号做傅里叶级数展开可得

(8)

式(8)中,A0表示直流分量,系数An可由下式求得

(9)

当目标与引信之间存在相对运动时,联立式(8)、式(9)求得差频信号SF(t)的傅里叶级数展开式为

SF(t)=Sodd(t)+Seven(t),

(10)

式(10)中,

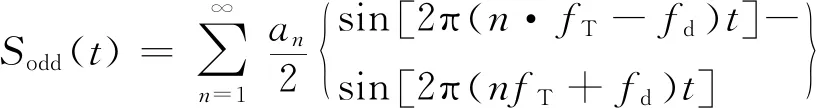
(11)

(12)

(13)

(14)

为了能够更加直观地观察谐波信号的特征,设置相应的仿真参数得到2次谐波信号幅值随引信与目标相对距离的变化曲线如图2、图3所示。

图2 2次谐波信号幅值随距离变化曲线Fig.2 Variation curve of the second harmonic signal amplitude with distance

图3 10 m附近局部放大图Fig.3 Local enlarged image around 10 m

仿真参数设置：载频fc为3 GHz,调制频偏B为17 MHz,调制频率fT为150 kHz,相对速度v为300 m/s,不考虑信号能量随传播距离变化而衰减。

2 数字包络检波算法实现

2.1 Hilbert检波及正交检波

FMD引信系统中2次谐波信号表达式为

S2(t)=E(t)·F(t),

(15)

式(15)中,E(t)为2次谐波信号待检包络,F(t)表示复合正弦波信号。

E(t)=sinc{π-πBτ(t)}+sinc{π+πBτ(t)},

(16)

F(t)=cos(ω1t)+cos(ω2t),

(17)

式(17)中,ω1、ω2表示不同角频率,ω1=2π·(2fT-fd),ω2=2π·(2fT+fd)。

同步检波用与F(t)同频同相的参考信号与之相乘,然后利用低通滤波滤除高频分量得到包络信号,由于F(t)不是单频信号,不具备适用条件。正交检波将待检波信号分为两路,分别与相位相差90°的参考信号相乘,利用低通滤波滤除高频分量,对两路输出信号平方求和得到包络信号。针对2次谐波信号S2(t)进行正交检波得到输出信号表达式为

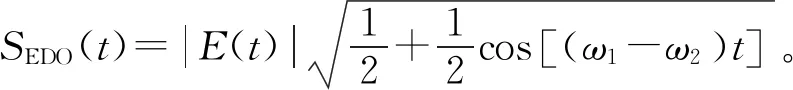
(18)

Hilbert检波通过对待检波信号做Hilbert变换,得到具备90°相移的输出信号,对两者平方求和得到包络信号。针对2次谐波信号S2(t)进行Hilbert检波检波得到输出信号表达式为

(19)

观察式(18)、式(19)可知,由于F(t)不是单频信号,不论是利用正交检波还是Hilbert检波对谐波信号进行检波,都不能正常实现检波功能。

2.2 基于EMD的数字检波算法

结合谐波信号表达式与谐波信号幅值随距离变换曲线及局部放大图可以看出,谐波信号为幅度受sinc函数调制的正弦波。

1) 算法原理

经验模式分解(EMD)方法,是一种通过特殊的迭代规则,将信号分解成一系列本征模态函数之和的操作方法。EMD方法的基本步骤：找到信号的极值点,用一条曲线将极值点连接起来构造包络,从原信号中减去包络均值。重复上述过程,直到包络均值为零。借鉴EMD方法,即通过找到信号的极值点,利用极值点信息做最小二乘曲线拟合对信号进行检波。

从图3局部放大图可以看出,除了位于信号包络上的极值点外,还存在大量冗余极值点。为了达到良好的检波效果,必须减小冗余极值点的影响。观察图3发现,各极值点之间遵循单调变化的趋势,因此可以通过对极值点做线性插值之后再次寻找极值点来减少冗余极值点的数量,重复这一操作可以减小冗余极值点对检波的不利影响。

检得峰值后,利用峰值信息做最小二乘曲线拟合来实现检波。最小二乘法,又称最小平方法,通过使估计数据与实际数据之间误差的平方和达到最小来寻找与实际数据最为匹配的函数表达式。最小二乘曲线拟合的基本原理如下：

对于未知信号x(t),已知其在时刻t1,t2,t3,…,tn(n为正整数)对应的信号值x(t1),x(t2),x(t3),…,x(tn)。现构造m次多项式Pm(t) (m为正整数)表达式如下：

(20)

为了使Pm(t)与未知信号x(t)达到最佳匹配度,Pm(t)的多项式系数ak的取值必须使得下式达到最小值：

(21)

2) 算法流程

图4是数字包络检波算法的流程图。

图4 数字包络检波算法流程图Fig.4 Flow chart of digital envelope detection algorithm

具体的步骤说明如下：

步骤1) 将原始信号输入存为信号1;

步骤2) 对信号1寻找峰值并存储信号1的峰值信息;

步骤3) 利用步骤2)中获得的峰值信息做线性插值,得到信号2;

步骤4) 将信号2存储覆盖信号1并跳转到步骤2),循环操作这一步骤k次,利用谐波信号的先验知识取得k的预设值,若k达到预设值,执行步骤5)。

步骤5) 利用步骤3)中存储的峰值信息做曲线拟合得到检波信号并输出。

3 仿真实验结果

3.1 Matlab仿真验证

按照2.2节设置仿真参数,生成2次谐波信号幅值随引信与目标相对距离的变化曲线如图5(a)所示,图5(b)为Hilbert数字检波方法的检波结果,图5(c)为基于EMD的数字包络检波算法的检波结果。从图中可以看出,针对FMD引信系统谐波信号,传统的数字检波方法无法正常实现检波功能,而基于EMD的数字包络检波算法对于谐波信号可以正常实现检波功能。

图5 2次谐波信号幅值随距离变化曲线及对应检波信号对比图Fig.5 Variation curve of the second harmonic signal amplitude with distance and corresponding comparison chart of detection signal

3.2 SystemVue/ADS联合仿真验证

为了更加贴近实际场景,进一步验证基于EMD的数字包络检波算法的有效性,利用仿真软件SystemVue建立调频多普勒定距引信系统模型,如图6所示。信号源模块生成三角调频连续波作为发射信号,在回波信号模块中,发射信号经过上变频、延时,考虑收发天线性能参数影响及信号能量随传播距离变化的影响,生成回波信号。添加噪声模块,噪声与回波信号通过混频模块去载频生成差频信号,经由ADS/SystemVue交互接口将差频信号输入ADS信号处理模拟电路中。

图6 基于SystemVue建立的调频多普勒引信定距系统模型示意图Fig.6 Schematic diagram of the FM doppler fuze ranging system model based on SystemVue

图7为利用模拟电路仿真软件搭建的调频多普勒引信定距系统的信号处理电路流程框图。经由ADS/SystemVue交互接口,端口1输入SystemVue产生的差频信号,经过双峰滤波器滤波使信号能量集中于2次谐波与4次谐波。谐波信号经过混频器与低通滤波器产生所需的多普勒信号,经由ADS/SystemVue交互接口,端口2向SystemVue输出多普勒信号,在SystemVue中经由数字包络检波模块得到数字检波信号。端口3输出由模拟电路检波得到的检波信号。

图7 基于ADS建立的调频多普勒引信定距系统的信号处理模拟电路流程框图Fig.7 Block diagram of the signal processing simulation circuit of the FM doppler fuze ranging system built on ADS

仿真参数设置：载频3 GHz,三角调频连续波调制带宽40 MHz,调制频率150 kHz,引信与目标相对速度300 m/s,初始距离20 m。

图8与图9分别为不考虑干扰信号与考虑高斯白噪声干扰的情况下, 4次谐波信号幅值随距离变化曲线及Hilbert数字检波方法检波结果与基于EMD的数字包络检波算法检波结果示意图。

图8 无干扰情况下,4次谐波信号及Hilbert检波信号、EMD检波信号幅值随距离变化示意图Fig.8 Schematic diagram of the variation of the fourth harmonic signal, Hilbert detection signal and EMD detection signal with distance in the absence of interference

图9 有干扰情况下,4次谐波信号及Hilbert检波信号、EMD检波信号幅值随距离变化示意图Fig.9 Schematic diagram of the variation of the fourth harmonic signal, Hilbert detection signal and EMD detection signal with distance in the presence of interferenc

从图8、图9中可以看出,针对FMD引信系统的谐波信号,传统的数字检波方法无法正常实现检波功能,而基于EMD的数字包络检波算法可以正常实现检波功能。

4 结论

对调频多普勒引信系统中谐波信号做数字检波时,谐波信号表达式较为复杂。而传统数字包络检波算法对于待检波信号预设条件为幅度受到调制的单频信号,所以传统数字包络检波算法无法正常实现调频多普勒引信系统检波。为了解决这一问题,提出一种基于EMD的数字包络检波算法,该算法相对于传统的数字检波方法,对待检波信号没有严格的表达式要求,对谐波信号可以正常实现检波功能。