某连续T梁桥静载试验检测分析

李 政 赵 恒 肖 珍

常德学院 湖南 常德 415000

1 项目简介

某城市立交桥全长391m，共3联，为（3×35）m+（4×45）m+（3×35）m预应力混凝土先简支后连续T型梁桥，横断面形式为3.0m人行道+6.5m(非机动车道+单位车辆进出车道)+11.5m机动车道+0.5m防撞墙+0.5m花槽=22m。桥梁照片、立面布置及第二联横断面布置图如图1-3所示。

图1 桥梁照片

图2 立面布置图（从上至下依次为第一、二、三联）

图3 第二联横断面布置图

2 静载试验

2.1 试验T梁

选择该立交桥第二联4×45m连续T梁中的一片45mT梁（第4跨左幅4#梁）进行静载试验，试验梁属边跨（第4跨）中梁，为裸梁，试验时按连续梁考虑。

2.2 试验荷载

（1）理论计算设计内力

根据《城市桥梁设计规范》（CJJ 11-2011）可知[1]，该桥梁汽车荷载按城-A级；人群荷载为3.6kPa。对试验梁进行理论计算可知梁设计弯矩如表1所示。

表1 试验梁跨中截面设计荷载弯矩值

（2）试验荷载

本次静载试验采用堆载钢筋方式进行模拟试验加载，拟采用1/2跨径布载方案。根据弯矩等效的原则，计算加载集度为q=32M/ (3L2)=30.9kN/m，则需要钢筋的重量为G=qL=680kN，即需要68吨钢筋。按每捆钢筋重2.3吨，则需要钢筋捆数30捆。

（3）加载效率

根据《公路桥梁荷载试验规程》（JTG/T J21-01-2015）的要求[2]，桥梁的静力试验按荷载效率来确定试验的最大荷载。在试验荷载作用下，试验梁控制截面的内力值及加载效率计算结果如表2所示。由此可见，试验梁加载效率满足规范要求。

2.3 测点布置

（1）变形测点：在两边支座及L/4、L/2、3L/4处两侧布置，共10个，变形测点布置详见图4所示，变形采用百分表量测。

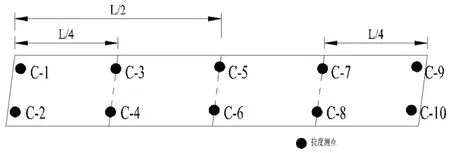
图4 T梁变形测点布置图

（2）应变测点：沿跨中截面的腹板布置，共4个，详见应变测点布置图5所示。

图5 应变测点布置示意图

（3）裂缝测点：试验前对各联各跨梁进行了全面详细的检查，未发现有明显裂缝存在。在整个静载试验过程中，应对试验梁的裂缝情况进行仔细观测，观测各级荷载作用下T梁裂缝情况。

2.4 加载方式

本次静载试验采用钢筋作为配重分三级进行加载。第一级加载，跨中20m长度内均匀加载16捆钢筋，2层布置；第二级加载，跨中20m长度内继续加载6捆钢筋，2层布置；第三级加载，跨中20m长度内继续加载6捆钢筋，3层布置，静载试验加载如图6-7所示。

图6 45m跨径T梁布载结构图

图7 试验梁加载示意图（单位：cm）

2.5 理论变形

经计算试验梁在各级荷载作用下，试验T梁在L/4、跨中、3L/4截面处变形及跨中梁底应变的理论计算结果如表3所示。

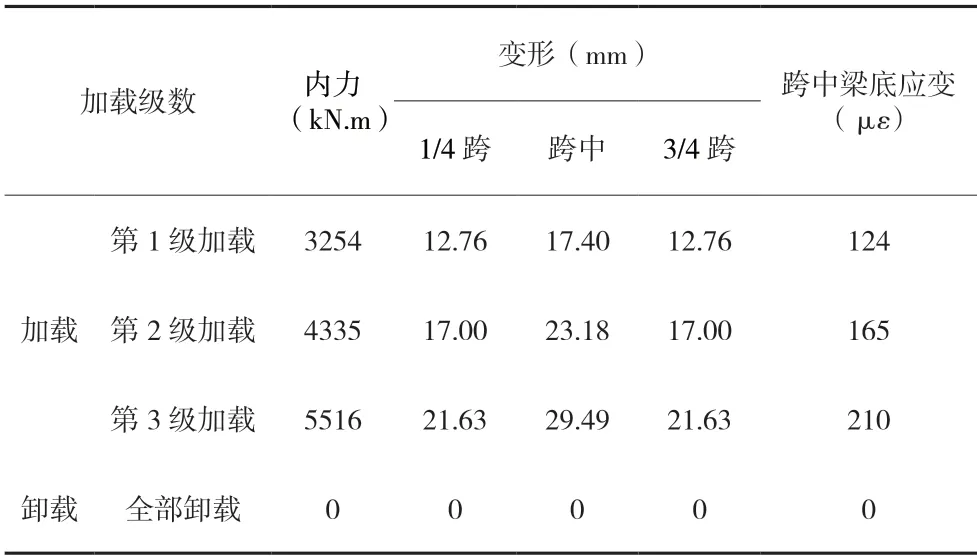
表3 控制截面变形及应力理论计算值

每施加一级荷载，持荷20分钟，记录各测点变形及应变；当荷载加至最大试验荷载后，持荷30分钟或梁体下挠不超过0.1mm/min，记录各测点的变形及应变，并检查梁体是否有裂缝发生。

2.6 试验终止条件

当试验过程中发生下列情况应中途停止加载[3-4]：

（1）控制测点应力、变形（或挠度）已达到或超过计算的控制值时；

（2）结构裂缝的长度或缝宽急剧增加，新裂缝大量出现或缝宽超过允许值的裂缝大量增多时；

（3）桥梁沿跨长方向的实测变形曲线分布规律与计算结果相差过大时；

（4）发生其它影响桥梁承载能力或正常使用的损坏时。

3 试验结果

3.1 应变检测结果

试验梁跨中截面腹板在不同荷载工况下的应力值，详见表4，试验梁的应变及变形实测值均小于理论值，且分布规律与理论计算一致。

表4 各应变测点微应变理论值与实测值

3.2 变形检测结果

通过静载试验，并考虑支座沉降的影响，可得到试验梁测点在各级荷载作用下的实测变形值，可知各点的实测变形值均小于理论计算值。各测点变形检测结果如表5所示。桥梁各测点的实测变形曲线与理论计算曲线一致（如图8所示）。

表5 各测点变形实测值和理论值比较表

图8 截面变形测试值与理论值比较图

3.3 裂缝检测结果

在整个加载、卸载过程中，未见试验梁参数开裂现象。

4 结论

通过对该立交桥进行静载试验，可得到以下结论：

（1）该桥梁的试验加载效率为98.3%，满足规范的要求。

（2）跨中截面腹板测点最大理论微应变值为210με，实测最大微应变为163变形，检校效率为0.776，其它各点的实测微应变值均小于理论计算值，各点的残余应变均小于20%，应变满足规范的要求。

（3）跨中截面最大理论计算变形值为29.49mm，实测最大变形为22.54mm，检校效率为0.764，其它各点的实测变形值均小于理论计算值，满足规范的要求。

（4）试验梁在试验荷载作用下梁体均未开裂，满足规范及设计要求。