预埋角钢连接件装配式梁板节点抗震性能试验

李浩东,张玉玲,贾高宗

(1. 安徽建筑大学 土木工程学院,安徽 合肥 230601; 2. 合肥供水集团有限公司,安徽 合肥 230011)

推进装配式建筑的使用满足碳达峰碳中和的要求,装配式结构中节点的性能直接影响构件的强度、延性等。为满足“强节点、弱构件”的设计原则[1],提高结构的变形性能,增强抵抗地震荷载的能力,国内外学者对装配式节点进行了深入研究。Ding等[2-3]对梁柱节点进行试验分析,得出现浇节点与装配式节点承载力基本相同,使用高强螺栓的装配式梁柱节点具有更高的承载力与更好的抗震性能。Parastesh等[4]对延性受弯节点进行试验研究得出预制节点的耗能能力明显高于现浇节点。夏康等[5]对2组不同轴压比的叠合梁-预制剪力墙节点进行低周往复加载试验,并与现浇节点进行对比,研究表明预制剪力墙节点也具有较好的抗震性能,并在此基础上提出了适用于该节点的四折线恢复力模型。

传统的出筋叠合板运输不便,设计时精细化工作量大,本文提出一种带弯筋的角钢,角钢筋外伸至预制混凝土板外,利用与现浇混凝土与钢筋的握裹性,增加叠合板的整体性。为探究带角钢的装配式梁板节点的抗震性能,与现浇梁板节点进行对比,分析2种梁板节点的抗震性能,本文对2组节点的抗震性能参数进行分析,依据试验结果数据提出一种适合该节点的“三折线”骨架曲线模型。

1 试验概况

1.1 试验设计

关于梁板节点的研究,多考虑的是平面外荷载及面内与钢梁平行方向的荷载对节点的影响,但当地震发生时,垂直于板拼缝方向的惯性力同样可能对节点造成一定的影响。地震带来的惯性力实际上与楼层质量、地面震动加速度及结构的强度等有关,这些情况下装配式梁板节点是否具有与现浇节点相近的横向承载能力、预制层与现浇层是否会因层间力传递而发生破坏均值得探究。

本文利用拟静力试验,模拟梁板节点在垂直于拼缝方向的受力情况。施加横向低周往复加载,可以模拟出产生的横向地震作用,此时梁板节点受水平震动,惯性力随之发生方向改变,与实际地震情况相比,仅考虑了横向地震作用对梁板节点带来的影响,得出梁板节点的横向承载能力,暂未考虑竖向地震荷载产生的影响。

1.2 构件设计

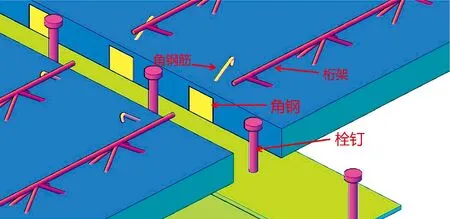
文中设计了2组梁板节点,第一组为现浇梁板节点,编号SJ-1;第二组为装配式梁板节点,编号SJ-2。2组节点的混凝土强度均为C30,钢梁上部混凝土板平面尺寸为1 320 mm×800 mm,钢梁截面尺寸为HM316 mm×200 mm×6 mm×8 mm,梁上焊接栓钉型号为M16-100,间距为250 mm。叠合板中预制底板平面尺寸为800 mm×600 mm,搁置在钢梁上的长度为40 mm,预制底板侧边预埋3块角钢连接件,角钢底面与钢梁焊接,预埋间距为200 mm,角钢规格为∟50 mm×32 mm×4 mm,角钢上的钢筋选用B8,如图1所示。

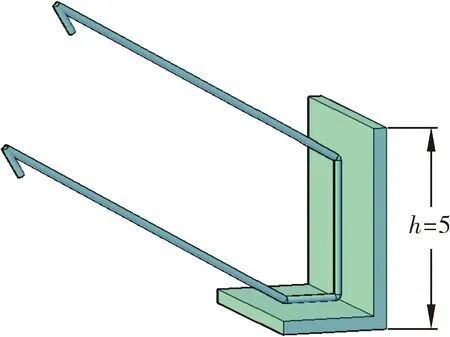
图1 角钢

叠合板内放置钢筋桁架,加强混凝土之间的连接,钢筋桁架的上弦筋采用B10,下弦筋为B8,腹杆为A6。叠合板内放置钢筋桁架,加强混凝土之间的连接,钢筋桁架的上弦筋采用C10,下弦筋为C8,腹杆为A6。2组节点如图2～3所示。构件由安徽巢湖富煌钢构集团进行加工制作,运至安徽省建筑结构和地下工程重点试验室进行现场拼装、浇筑、养护。

(a) SJ-1尺寸

(b) SJ-1现场

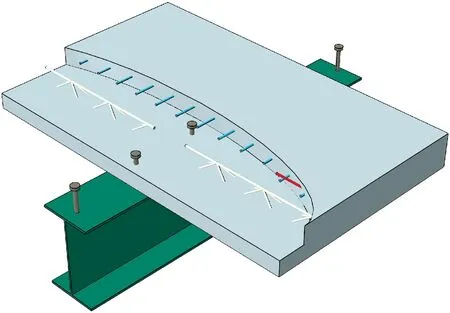
(c) SJ-1构造图2 SJ-1构件(单位:mm)

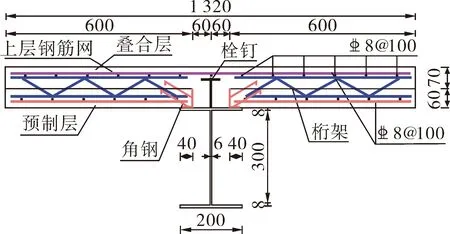
(a) SJ-2尺寸

(b) SJ-2现场

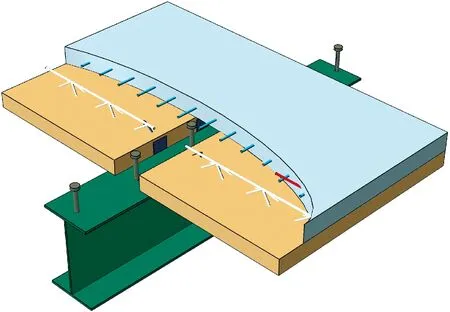
(c) SJ-2构造

(d) SJ-2节点图3 SJ-2构件(单位:mm)

1.3 材性试验

材料性能试验采用电液伺服压力试验机进行,钢材选取Q235,主要材料性能指标列于表1～2。

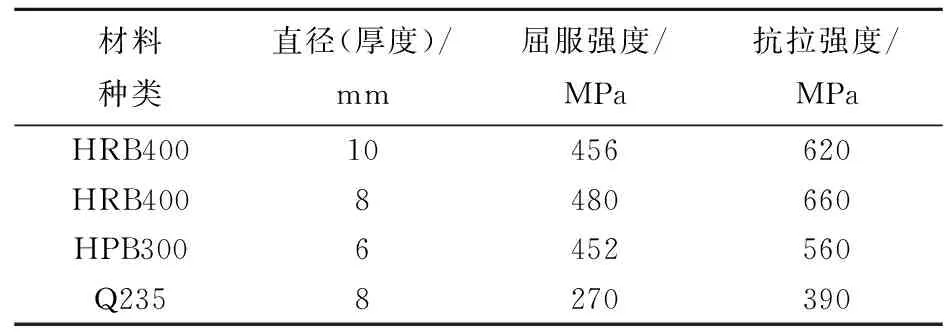
表1 钢材力学性能指标

表2 混凝土材料性能指标

1.4 试验过程与现象

1.4.1 加载设备

根据试验方案要求,加载设备采用量程为2 000 kN的MTS液压式伺服加载系统,加载设备如图4所示。

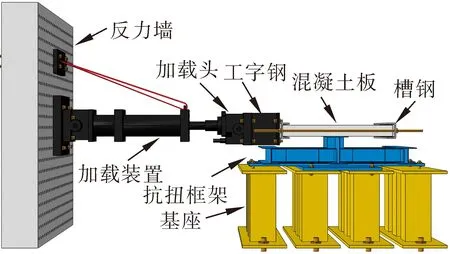
(a) 加载设备

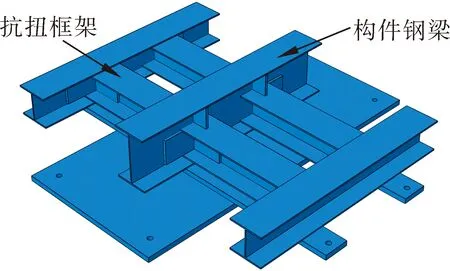
(b) 抗扭框架图4 加载设备

试验中用槽钢与螺杆来固定混凝土板的位置,工字钢一端与槽钢焊接,另一端与MTS的加载头通过螺栓进行连接。钢梁与抗扭框架进行焊接,并在钢梁腹板处焊接加劲肋,框架与基座通过螺栓进行固定。通过以上方式既可以避免加载头的翘起,也可以防止混凝土板发生平面内扭转。试验过程中通过作动器施加荷载于槽钢,后通过螺杆传力对梁板节点构件施加往复荷载,规定作动器从左往右推为正方向,由右往左拉为负方向。

1.4.2 加载制度

试验采用横向低周往复加载模式,加载过程参照《建筑抗震试验规程》(JGJ/T 101—2015),为消除试验前加载装置间存在的间隙,对构件进行预加载,并检查相关设备是否正常工作,预加载完成后进入正式加载阶段。正式加载采用荷载-位移联合控制的方式,初始加载阶段为力加载,级差为5 kN,每级循环1次,当荷载位移曲线斜率明显变缓时,改用位移控制,位移加载级差为5 mm,每级循环3次。当承载力下降至极限荷载的85%或节点发生明显破坏时,试验结束。具体加载方式如图5所示。

图5 加载制度

1.4.3 试验现象

2组节点在试验过程中破坏现象基本相似,加载前期梁板交界面的混凝土板缓慢开裂,此时未发生明显滑移;加载中期核心区混凝土板侧表面裂缝发展速度较快,数量增多,混凝土板与钢梁间出现明显滑移现象;加载末期节点核心区混凝土发生明显破坏,栓钉发生剪切变形。

SJ-1加载前期无明显变化,加载至约+28 kN时,梁板交界处的混凝土板一侧出现第一条细微裂缝,裂缝宽度约为0.13 mm;随着荷载增加,板侧裂缝增多并不断向板面发展,加载至+48 kN时,侧边裂缝宽度约0.63 mm,混凝土板与钢梁间裂缝增大,出现明显脱离现象;加载至+90 kN时,荷载-位移曲线斜率较之前变缓而后呈上升趋势,此时节点发生屈服,屈服位移约为9.99 mm;改用位移加载,此时裂缝发展较迅速,裂缝条数增多;加载至+16.66 mm时,正向达到极限荷载,继续加载至-22 mm时,此时负向达到极限荷载,承载力开始下降,继续加载至-27 mm时,板顶混凝土被压碎,板底混凝土开裂,栓钉有明显的剪切变形,试验结束。试验现象如图6所示。

图6 SJ-1试验现象

SJ-2加载前期无明显变化,加载至约+30 kN,梁板交界处的混凝土板一侧出现首条水平裂缝,继续加载至+36 kN时,侧边出现第1条竖向裂缝,裂缝宽度约为0.12 mm;板侧裂缝向上延伸后水平延伸,如图6(a);继续加载至+90 kN时,荷载位移曲线明显变缓,此时节点屈服,板底混凝土有脱落,板顶出现裂缝;改用位移进行继续加载,加载至+15.55 mm时,达到正向极限荷载,当加载至-21.12 mm,负向达到极限荷载;继续加载,承载力有明显下降,但下降幅度不大,加载至-26.99 mm时,板底混凝土被压溃,板面出现贯穿裂缝,栓钉发生剪切变形,节点发生破坏,试验结束。试验现象如图7所示。

图7 SJ-2试验现象

1.4.4 试验结果分析

对比2组节点的破坏现象,均经历开裂、屈服、破坏3个阶段。梁板节点在试验过程中受水平集中力作用,节点核心区会产生偏心弯矩,该弯矩会导致节点核心区混凝土及栓钉剪力连接件发生变形破坏。一旦核心区发生破坏,混凝土板发生翘曲,此时偏心距变大,偏心弯矩也会增大,往复荷载作用下,栓钉周围混凝土存在应力集中的现象。SJ-1为整体浇筑,所以在混凝土板产生裂缝后,受压区高度变小,导致混凝土板顶部受压区混凝土被压碎。而SJ-2因后浇混凝土与预制混凝土板接缝处力学性能较弱,在栓钉周围局部混凝土会先开裂,导致栓钉处混凝土最终先被压碎。2组节点的初始裂缝均产生在梁板交界面处的混凝土板上,但SJ-2内因存在角钢与钢梁焊接,开裂荷载略大,随荷载继续增加,试验现象略有不同,SJ-1整体性较好,混凝土内部无薄弱面,裂缝从板侧中部开始向上延伸,而SJ-2存在新旧混凝土交界面,裂缝则是从新旧混凝土交界面处开始率先产生并向上延伸。

2 抗震分析

2.1 滞回曲线分析

图8为2组节点的滞回曲线,对2组滞回曲线进行分析:加载初期,节点构件未产生裂缝,此时荷载-位移曲线近似一条直线段,随荷载增加,有细微裂缝产生,此时荷载-位移曲线呈非线性关系,但滞回环并不明显,曲线的包络面积也较小,故近似可视为线性关系[6],卸载过后,滞回曲线基本都回归原点,变形基本恢复,无明显残余变形;加载中期,荷载-位移呈明显非线性阶段,此时节点屈服,滞回环明显张开,包络面积开始变大,滞回曲线在卸载后不能回到原点,已存在明显残余变形;加载后期,滞回环闭合后面积达到峰值,在达到极限荷载后,节点承载力开始下降,下降段较平缓。

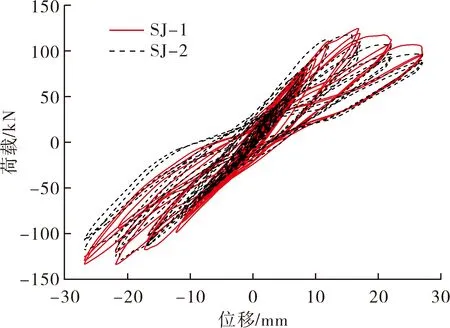
图8 滞回曲线

2组节点的滞回曲线均有“捏缩”现象发生[7],这是因为在低周往复荷载作用下节点核心区混凝土开裂,内部钢筋产生偏移,栓钉作为柔性连接件,会使混凝土板与钢梁产生相对滑移;2组节点的滞回曲线均表现为反“S”形,说明节点受滑移影响较大[8],且两组曲线具有明显不对称性,正负向的极限荷载并不在同一级位移中出现。

2.2 刚度退化曲线

刚度退化实际上是节点产生疲劳损伤及栓钉抗剪连接程度下降的宏观表现;随疲劳循环次数增加,节点刚度退化规律呈明显单调递减趋势[9]。用环线刚度计算公式(1)来计算2组节点的刚度退化曲线,即

(1)

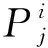
图9为2组节点的刚度退化曲线,节点发生屈服前,刚度退化速率较快,屈服后,刚度退化速率变缓,这是因为低周往复荷载下,混凝土会产生裂缝,钢筋发生塑性变形,材料产生疲劳损伤,刚度迅速下降。对比两组节点,SJ-1的初始刚度略大,但2组节点退化规律基本相同,说明节点形式对刚度退化无明显影响,刚度退化完成后,2组节点的正向刚度均小于负向刚度。

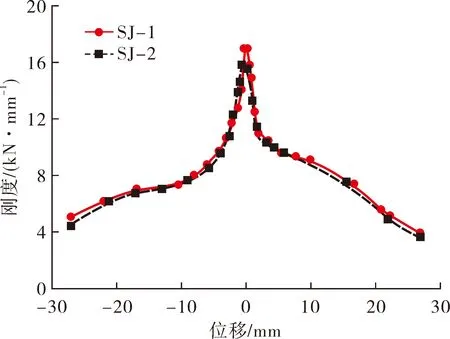
图9 刚度退化曲线

2.3 延性分析

延性系数能表征节点塑性变形的能力,用式

(2)计算节点延性系数,即

μ=Δu/Δy,

(2)

式中:Δu为构件的极限位移,是承载力下降至极限荷载的85%时或构件发生破坏时的相应位移;Δy为构件的屈服位移,文中屈服点的选取采用等面积法。

试验得到2组节点的特征点及延性系数如表3所示,现浇节点与装配式节点的延性系数分别为2.34与2.45,均大于2.0,说明该种梁板节点的延性良好,且正向延性系数略大于负向延性系数。

表3 节点特征点及延性系数

2.4 耗能性能

节点的耗能能力反映在承受地震荷载作用时吸收能量的多少,参照文献[10],对结构耗能进行计算,耗能计算如式(3)～(5)所示。

E=EABC+EACD,

(3)

(4)

(5)

现绘制位移-阶段耗能与位移-累计耗能如图10所示,图中横坐标位移取同一滞回环峰值位移绝对值的均值。分析2组节点的阶段耗能与总耗能,发现在加载初期,耗能能力弱,吸收能量少;加载中期,滞回环面积增大,吸收能量较多,随滞回环愈加饱满,耗能迅速增加;加载末期,随位移增加,SJ-1承载力下降缓慢,最后两级位移加载的阶段耗能无明显下降,但SJ-2承载力下降较SJ-1快,最后两级位移加载的阶段耗能下降较明显,总耗能在位移加载结束后达到峰值。

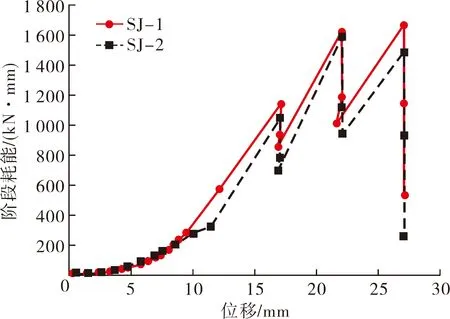
(a) 阶段耗能

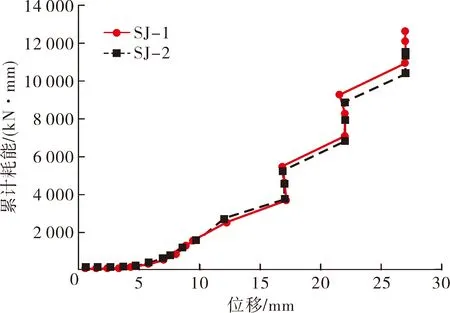
(b) 累计耗能图10 耗能能力

在荷载控制阶段,2组节点的耗能能力基本相同,进入位移控制阶段,同级位移加载时会出现承载力退化现象,这是因为节点构件在同级循环荷载作用下,会出现累积的材料疲劳损伤。对比2组节点的累计耗能,SJ-1略大于SJ-2。

3 骨架曲线

为准确研究梁板节点在地震荷载作用下的抗震性能与力学性能,对试验中2组节点的骨架曲线进行分析,并针对该类梁板节点建立一种用数学模型来描述的实用型骨架曲线模型,该模型既可作为在实际工程中的预测模型。

3.1 骨架曲线分析

骨架曲线是滞回环中峰值荷载的连线,能反映节点的极限荷载、变形能力等性能。如图11所示,2组节点骨架曲线均呈“S”形,表明节点经历了弹性阶段、弹塑性阶段、破坏阶段[11]。

图11 骨架曲线

1) 2组节点的骨架曲线在加载初期呈线性关系,此时处于弹性阶段;后达到屈服后,斜率有所下降,骨架曲线呈非线性关系,此时处于弹塑性阶段;荷载继续上升,骨架曲线达到峰值点,也是节点的极限荷载点,后节点进入破坏阶段,承载力开始下降。对比2组节点的承载力下降情况,SJ-1的承载力下降较SJ-2更为缓慢,说明SJ-1在发生破坏时仍能表现出较好的承载能力。

2) 对比2组节点的骨架曲线可知,SJ-1和SJ-2的极限承载力相差不大,正向极限荷载分别为123.44、116.91 kN,正向破坏荷载分别为峰值荷载的85.7%和81.4%,负向极限荷载分别为-135.51、-130.26 kN,负向破坏荷载分别为峰值荷载的93.6%和83.4%。加载过程中正向残余变形大于负向残余变形,导致每组节点的正向极限荷载均比负向低10%左右,说明初始加载顺序对节点的疲劳损伤有一定影响。骨架曲线的正向与负向变化规律相似,说明2组节点在正、负向有着相似的力学性能和抗震性能[12]。

3.2 建议的骨架曲线模型

常见的骨架曲线模型有曲线型与折线型,相对来说曲线型与实际试验结果更为相似,但折线型模型更方便计算。为消除不同设计参数带来的差异,将2组节点的骨架曲线进行无量纲化处理,如图12所示,无量纲化处理后的曲线横坐标为P/Pm,纵坐标为Δ/Δm,2组曲线呈现相似的变化规律,特征点的取值基本上相同,弹性阶段与弹塑性阶段均近似重合为同一条直线,为此提出一种能同时表示2组节点骨架曲线的数学模型。考虑节点退化经历3个阶段,因此该文建议的骨架曲线模型采用考虑刚度退化的“三折线”模型表示,确定其3组特征点尤为重要,3组特征点分别为屈服点(Δy,Py),极限点(Δm,Pm),破坏点(Δu,Pu)[13]。对2组节点的试验数据进行无量纲化,无量纲化后的数据以假定屈服点,极限荷载点和破坏点为分界点,进行回归分析,得到骨架曲线模型如图13所示。

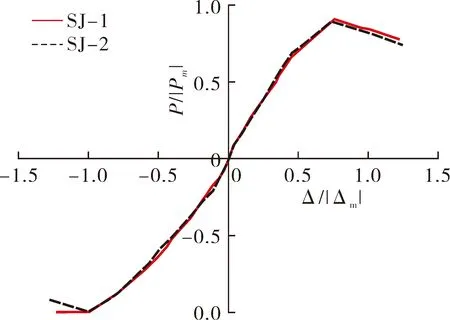
图12 无量纲化曲线

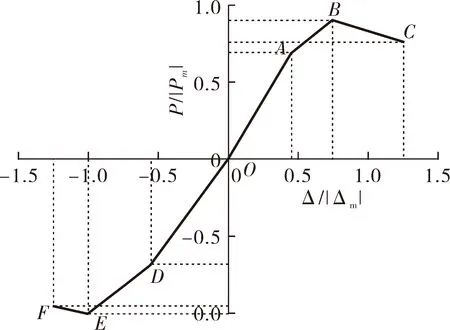
图13 建议的骨架模型曲线

骨架曲线模型的OA段与OD段由无量纲化曲线屈服前的数据点拟合而成,因为弹性阶段近似为一条直线,此时直线斜率表示为构件的初始刚度。AB段与DE段为弹塑性阶段,由屈服点到极值点之间的数据点拟合而成,斜率表现的是弹塑性刚度。BC段与EF段是破坏阶段,由极值点后到破坏点之间的数据点拟合而成,斜率表现的是考虑退化的弹塑性刚度。根据三折线曲线的特征,所有数据均由线性拟合而成。

回归拟合得到的骨架曲线方程如表4所示。为验证骨架曲线模型的准确性,将2组节点的特征点数据代入建议的骨架曲线方程中,将得到的理论计算结果与试验结果进行对比。对比结果如图14所示,发现两者具有较高的吻合度,表明此数学模型在实际工程中具有良好的可参考性,能较好反映梁板节点的荷载与位移在整个受力过程中的变化关系。

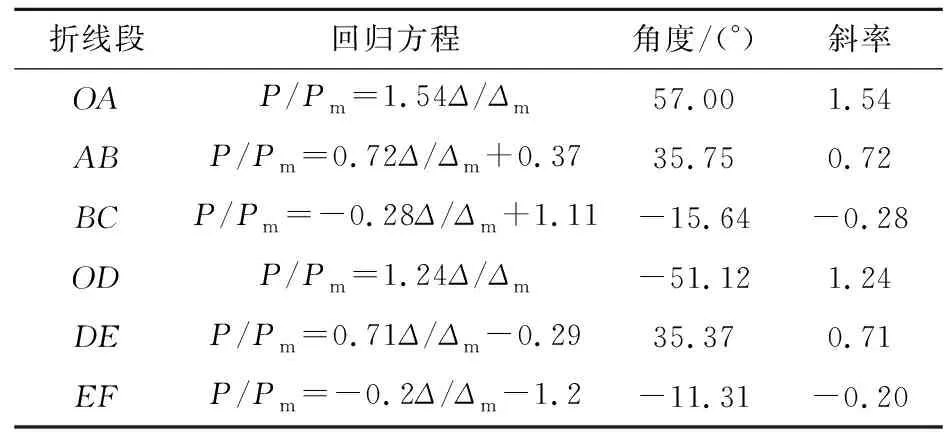
表4 回归得到的三折线骨架曲线方程

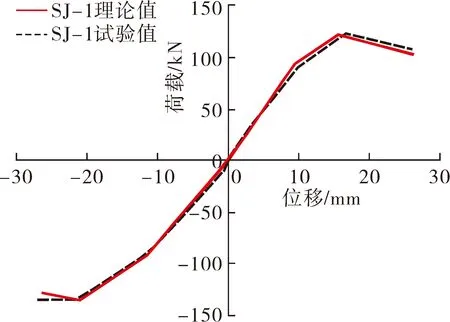
(a) SJ-1

(b) SJ-2图14 试验与理论骨架曲线对比

4 结论

1) 2组节点均发生延性破坏,试验结束时,节点核心区混凝土破坏,栓钉发生较大的剪切变形。但由于节点构造不同,裂缝位置及混凝土板的破坏形式有差异。

2) 2组节点的滞回曲线均呈反“S”形;现浇节点初始刚度较大,但2组节点的刚度退化趋势,耗能变化规律基本相同,延性系数相差不大,体现出相似的抗震性能。

3) 2组节点的骨架曲线形状相近,均为“S”形,都经历弹性阶段,弹塑性阶段和破坏阶段,且极限承载力无明显差异;利用本文建立的骨架曲线模型方程进行理论计算后的结果与试验结果吻合度较高。

4) 综上,装配式梁板节点与现浇节点体现出了相似的力学性能与抗震性能,本文的试验研究可为该类梁板节点的抗震设计提供参考,提出的模型可作为该节点恢复力研究的基础。