一类生产库存系统的最优控制策略

李丽花, 罗胜胜

(1.上海电力大学, 上海 200090; 2.上海伟陈贸易有限公司, 上海 200443)

生产库存管理对于企业的生产和经营活动特别重要。若生产过多,产品积压或腐坏,既增加库存成本,又不利于企业发展。若生产过少,供不应求,达不到效益最大化。因此,采用合适的生产库存策略,对于企业的发展具有一定的意义。

自从1935年生产库存模型被创立以来,生产库存系统的优化管理引起了研究者的广泛关注。1952年,最优控制理论被应用于生产库存系统的最优管理,此后诸多学者在这方面进行了深入的研究。对于输入有界的生产库存系统,BRADSHAW A和EROL Y研究了最优控制策略[1]。基于古典最优控制理论,学者们对需求依赖于库存水平[2-3]、易腐品[4-7]和具有产品返回[8-9]等各种类型的生产库存系统进行了研究。吴波[10]研究了在可以缺货情况下供应商和销售商联合生产的库存模型 。对于一类服务员休假的生产服务库存模型,徐浩等人[11]进行了稳态分析,并给出了最优生产策略。

文献[4]建立的生产库存模型中,假设需求为时间的下降线性函数。在实际生活中,往往价格越高,需求越低。因此,本文对文献[4]中的生产库存模型进行了改进,假设需求是价格的下降线性函数,结合产品需求和腐坏对库存的影响,并在目标函数中引入了产品的征税,建立了一类易腐品生产库存系统的最优控制模型。利用古典最优控制理论中的极大值原理,得到了最优控制策略。与已有文献相比,本文所建立的生产库存系统与实际更相符。

1 问题描述

现假设有一个仅生产一种产品的工厂,在任意t时刻该工厂产品的需求率是D(t),产品的实际生产率是u(t),腐坏率是θ(t),工厂的库存量是x(t),设T为大于零的常数,则系统的状态方程可以用以下微分方程来描述:

(1)

初始条件为

x(0)=x0

(2)

设生产率u(t)有上、下限,即存在常数U1和U2,使得

U1≤u(t)≤U2

(3)

设常数μ和b分别表示市场的潜在规模和价格敏感指数,μ>b,b>0,考虑需求率D(t)是t时刻销售价格p(t)的线性函数,即它们满足

D(t)=μ-bp(t)

(4)

实际意义上需求率大于零,即D(t)>0,由式(4)有

(5)

将式(4)代入式(1)中,得

(6)

设常数c和h分别代表单位生产成本和单位库存消耗成本,c>0,h>0,a为政府出台的关于单位产品所征的税,a>0。由此可建立以产品的总销售额为目标函数,即

hx(t)-au(t)}dt

(7)

本文所研究的最优控制问题为:寻找最优控制u*(t)和p*(t),满足微分方程式(6),在式(2)、式(3)和式(5)成立的同时,使得性能指标式(7)取得极大值。

引入拉格朗日乘子λ,则哈密尔函数为

H[t,x(t),u(t),p(t),λ(t)]=

p(t)[μ-bp(t)]-cu(t)-

hx(t)-au(t)+λ{u(t)-

[μ-bp(t)]-θ(t)x(t)}=

[μ-bp(t)][p(t)-λ]+

(λ-a-c)u(t)-[h+λθ(t)]x(t)

(8)

根据极大值原理,其最大值表示为

H*[t,x(t),u(t),p(t),λ(t)]=

(9)

由式(9)可得

(10)

(11)

根据最优控制的正则方程,可以得到

(12)

由式(12)可以求出λ(t)并判断其取值范围,结合式(10)、式(11),可以把解分成以下6种情况。

(1) 当λ≤-μ/b,则p*(t)=0,u*(t)=U1,可得:

(13)

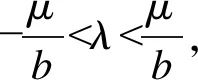
(14)

(3) 当λ=c+a,则p*(t)=b(c+a)/2b,u*(t)∈[U1,U2],此种情况下,显然有

(15)

利用式(2)和式(6),可得:

(16)

(4) 当c+a<λ<-μ/b,则p*(t)=(bλ+μ)/2b,u*(t)∈U2,可得:

(17)

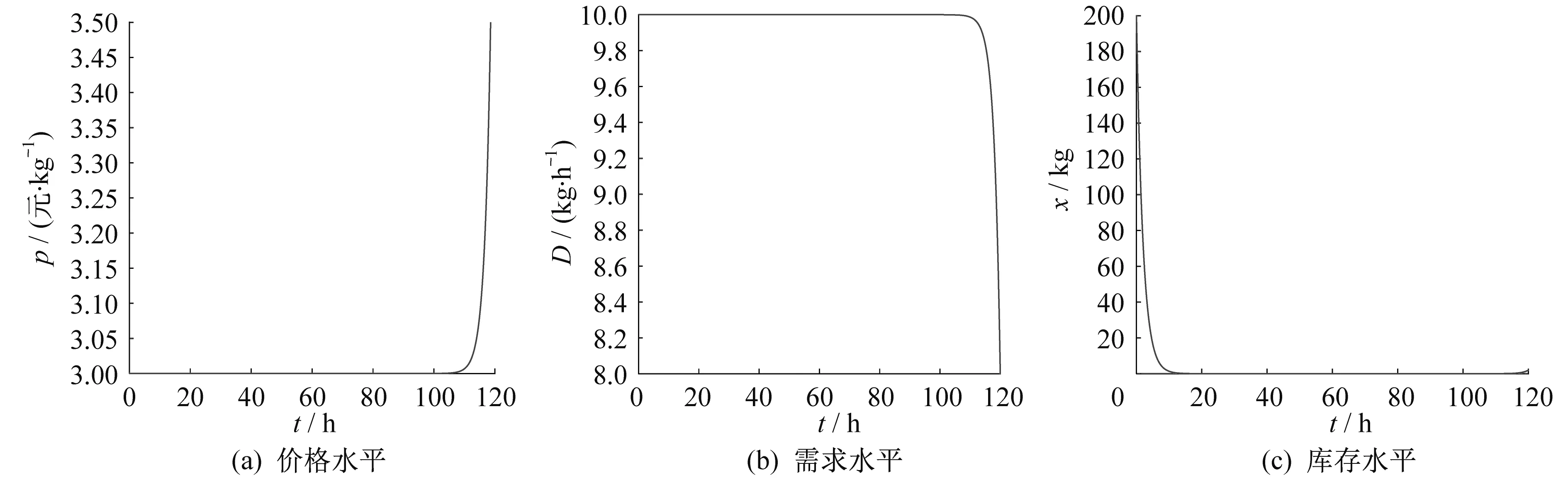
(5) 当μ/b≤λ

(18)

(6) 当λ≥max(μ/b,c+a),则p*(t)=μ/b,u*(t)=U2,可得:

(19)

可以通过式(13)～式(19)分别求出其对应的x*(t)。

对于上面讨论中的情形(3),由于λ(t)是关于t的函数,故其满足此情形的时刻仅为一瞬间,也就是说它是某种情形到另一种情形的一个过渡状态,故对此情形不作较多考虑。

2 具体算例

现假设生产库存系统式(1)～式(6)中的各个参数分别为x0=200 kg,T=120 h,U2=25 kg/h,U1=10 kg/h,θ=0.5 kg/h,c=2元/kg,h=1元/kg,b=2,μ=16 kg/h,a=1元/kg,求该生产系统的最优生产率u*(t)、销售价格p*(t)和系统的库存量x*(t),使得性能指标式(7)取得极大值。

解:利用式(12),得:

(20)

由式(20)可知:

(21)

由式(10)和式(11),可以得到:

(22)

故此问题对应前文讨论的情形(2),利用式(14)可以求得相应的状态方程。利用MATLAB可分别作出价格p、需求率D和库存量x关于时间的价格水平图、需求水平图和库存水平图。由模型建立的出发点易知,倘若改变价格敏感指数b,那么需求率D也会发生变化。设b=2为状态1,b=1为状态2,两种状态对应的价格水平、需求水平和库存水平分别如图1和图2所示。

图1 状态1价格水平、需求水平和库存水平

由图1可以看出:库存以较大的速度减少,而价格没有什么变化,因而需求不变;当时间趋近T时,库存以微弱势头回升,而此时价格也开始上升,进而需求开始下降。

比较两个状态相对应的图1和图2可以发现,两者的各个走势基本相同。虽然价格变得较高,因而导致需求较低,但是总的库存量相差不多。

3 结 语

本文研究了一类易腐品的生产库存问题。利用企业中生产和库存之间的关系,建立了库存量、生产率和销售率的动态系统方程。利用最优控制理论中的极大值原理,得到了该模型的最优生产库存策略,并将所得结果应用于具体算例。本文所得结论对于实际生产中的库存管理和销售决策具有一定的参考作用。