双导堤工程下潮汐汊道与海岸潟湖地貌稳定性

匡翠萍， 范家栋， 董智超， 韩雪健

（1. 同济大学 土木工程学院，上海 200092；2. 中交第一航务工程局有限公司，天津 300461；3. 中交天津港湾工程研究院有限公司，天津 300222）

海岸潟湖作为一种特殊的海岸地貌，其本身是一片封闭或半封闭的水域，通过潮汐汊道同外海连通，上游常有陆地河流汇入［1］。基于海岸潟湖的特殊地貌条件，其稳定性受河流水文情势和海洋水文情势共同影响。作为一类重要的海岸带湿地，海岸潟湖在稳定的水文条件下能够产生经济、社会、环境等多重效益，而水文条件一旦遭到破坏，海岸潟湖在地貌演变的进程中就存在消亡的风险［2］。无论是人类活动还是气候变化，都会对潟湖地貌的演变趋势产生一定影响［3-5］。近年来，我国坚持海陆统筹、以海定陆，积极推动滨海湿地整治修复，以遏制滨海湿地资源退化趋势。针对海岸潟湖，综合整治修复的关键即促使其水文条件和地貌演变恢复或维持在稳定状态，因此关于海岸潟湖地貌稳定性的研究尤为重要。

国内对于潮汐汊道的关注，始于1984年由任美锷和张忍顺所提出的“汊道-潮盆系统”（Inlet-basin system）的概念［6］，潮汐汊道类型则是根据该系统中纳潮水域的不同来划分的，例如潟湖系统中的潮汐汊道即为潟湖型潮汐汊道（以下简称潮汐汊道）。潮汐汊道连通潟湖和外海，对潟湖系统的水沙格局起主导作用，所以潟湖地貌演变的稳定性同潮汐汊道自身稳定相关［7-8］。国外学者对潮汐汊道稳定性的研究可以追溯到1931年，O’Brien［9］利用经验参数构建了以纳潮量P和潮汐汊道口门段平均海面下均衡过水断面面积A（以下简称过水断面面积）表征的相互关系以判定潮汐汊道稳定性，即P-A关系，经验参数可以由相关数据分析、拟合所确定，针对不同的研究区域有其相对应的数值［10］。对于某一潮汐汊道，如果其纳潮量和过水断面面积遵循此关系，则认为该潮汐汊道地貌形态稳定。据此，张侨民［11］、高抒［12］、张忍顺［13］分别先后对我国东海、南海以及黄渤海沿岸的潮汐汊道进行研究分析，并总结出对应的P-A关系如下：

需要注意的是，高抒在东海沿岸潮汐汊道的研究中给出P-A关系的基本单位是m，为统一单位以便后文对照分析，式（2）已由原式换算，故上式中纳潮量P和过水断面面积A单位业已统一，分别为km3和km2。鉴于潮型差异，Bruun［14］提出建立最大潮流量同过水断面面积的相互关系以进行稳定性计算。Aubrey和Weishar［15］指出潮汐汊道稳定性的变化体现在口门处的输沙能力，其取决于潮汐汊道纳潮量同潟湖淤积速率的相互关系，两者互为反馈。此后，Friderichs和Aubrey［16］进一步提出以床面特性判定潮间带地貌稳定性，若床面切应力同其临界侵蚀切应力一致，那么该区域地貌相对稳定。由于临界侵蚀切应力受底部流速控制，Xu等［17］结合Bruun以及Aubrey先前所提出的研究方法优化了断面最大流量Qm与过水断面面积A的相互关系，以作为潮沟系统稳定性的判定依据，其中断面最大流量即由底部流速推导得到，因此相较于P-A关系，Qm-A关系充分考虑了底摩阻的影响，尤其当潟湖系统内潮滩占比过高时，应用Qm-A关系判定稳定性更为有效。不过Xu等［17］基于河口、潟湖等地貌展开研究，其侧重于潮间带即潮沟系统发育区域的地貌稳定性研究，未对潮汐汊道的稳定性进行深入考量。

由于水文及地形条件的差异，潟湖稳定性的影响机制和潮汐汊道不完全一致。近期Kuang等［18］利用现场观测和数值模拟的方法，研究了七里海潟湖自1900年至2018年的长期演变过程，并指出潟湖内泥沙冲淤变化不仅受区域来水来沙条件影响，由海平面上升、人类活动以及径流量变化所造成的潮汐不对称性会加剧潟湖内部的泥沙淤积现象。在针对地貌稳定性影响机制的研究中，理想模型因其能够有效反映各参数对研究主体的影响过程而被广泛采用。Xie等［19］和Cong等［20］分别基于我国东海和渤海沿岸的相关资料，利用理想模型模拟了区域内潮汐汊道的地貌演变过程，并成功建立了P-A关系，两组模拟结果均显示地貌演变在模拟初期较为剧烈，随后趋于稳定。对于潟湖系统稳定性的研究，一般通过潮沟系统的发展情况表征，Iwasaki等［21］通过比较发现发现利用数值模拟的方法能够更精细地呈现潮沟系统发展过程。Marciano等［22］基于理想模型有效模拟了瓦登海多级潮沟系统的演变过程，并强调了初始地形对潮沟系统稳定性的影响。

此前基于七里海潟湖理想模型所开展的研究重点分析了泥沙特性、初始地形、径流条件对单一潮汐汊道的海岸潟湖系统地貌演变的影响机制［23-24］，结果表明临界侵蚀应力、临界淤积应力和泥沙沉速的增加均能够促使潮沟系统的发育达到稳定，即有利于潟湖地貌演变趋于稳定。在初始床面高程低于潟湖最低潮位的前提下，水深越大，湖内侵蚀作用越弱；径流量较小时，湖内侵蚀作用也相对较弱，表明在水动力条件较弱的情况下，潟湖地貌演变易于趋向稳定。在此基础上，当前研究将继续采用数值模拟的方法，通过改变理想模型的相关参数以确定潟湖系统达到地貌稳定所需时间，并建立相互关系以提供判定单一潮汐汊道的海岸潟湖稳定性的量化方法。最后，分别利用量化方法和泥沙净淤积量变化量推算各工况条件下潟湖地貌演变达到相对稳定的时间并进行比较分析。

1 区域概况

七里海潟湖地处河北省秦皇岛市昌黎县沿岸是我国华北地区最大的潟湖（图1a），通过新开口潮汐汊道同渤海相连，上游共有4条河流汇入（图1b），具备单一潮汐汊道的海岸潟湖特征。七里海潟湖的形成与典型潟湖地貌成因并不一致，李从先等［25］从沉积学角度将沙坝-潟湖系统细分为海侵型，海退型，稳定型和局部海侵型，可以发现海洋水文情势对该系统的自然状态起主导作用，在特定的外海条件下，沙坝将处于淤进、退蚀或相对稳定的状态，然而七里海潟湖的海岸沙丘群并非由滨外沙坝演变而来［26］。七里海原为淡水湖泊，因滦河泛滥，洪水倾泻，冲出水道入海，于是形成新开口潮汐汊道，由此具备海岸潟湖条件［27］。七里海潟湖在地貌演变过程中曾受建闸、围垦等影响，潟湖内部水体交换能力一度锐减［28］，后来通过开闸、疏浚等有效治理，并加以生态修复［29］，使得其水体交换能力得以恢复，当前潟湖实际水域面积达2.26×106m2。潮汐汊道入口所处秦皇岛海域受无潮点影响，涨落潮过程比较复杂，出现类似半日潮流变化，存在相邻高潮（或低潮）潮高不等现象，该海域M2分潮为最主要分潮流，其周期表现为规则半日潮流。潟湖水系包括赵家港沟、泥井沟、刘坨沟和稻子沟，均为发源于滦河以东高亢平原的季节性河流，流域面积为1.0×109m2，多年平均径流量为18.2×106m3。近年来，因降水量减少，汛期不能形成洪水，入湖径流量减少，甚至为0，正是由于潟湖上游径流规模较小，输沙量有限，所以其水流条件主要受潮汐汊道控制。即便如此，径流下泄依然对落潮流有促进作用。因此，七里海潟湖不仅具备单一潮汐汊道的海岸潟湖特征，还具有其特殊性，即受口门双导堤工程维持的潮汐汊道口门形态以及受河流水文情势影响的动力条件。孙伟富［1］以潟湖发育演变阶段作为分类指标，明确将七里海潟湖划定为青壮期潟湖，即潟湖当前自然状态可以维持冲淤相对平衡，该稳定状态极大程度上得益于其特殊性。

2 模型建立

应用丹麦水环境研究所（DHI）研发的MIKE21软件建立七里海潟湖理想模型，利用水动力和泥沙模块模拟七里海潟湖系统在不同参数条件下的地貌演变，相关计算方法可参见MIKE官方网站的用户手册（https：//www.mikepoweredbydhi.com/），在此不做赘述。以下是对理想模型的概化方法、网格布设、参数设置和泥沙输运计算原理的详细介绍。

2.1 模型概化

基于前期研究资料及经验证可靠的MIKE21数学模型［20，23-24，30］，首先对七里海及外海部分水域水沙动力过程进行模拟分析。潟湖地形，水流流速，含沙量，床面表层泥沙粒径等参数取自河北省地矿局第八地质大队于2016年现场测量所得数据，其中地形数据采用RTK（Real-time Kinematic）和SOKKIA全站仪测量，水流流速与含沙量通过ADCP（Acoustic Doppler Current Profiler）设备测得，床面表层泥沙粒径则是利用激光粒径分析仪对表层床沙样本进行分析后获得，另外，岸线资料采用2018年通过卫星遥感所采集得到的岸线数据（图1b）［24］。实际模型通过耦合水动力模块、波浪模块以及泥沙输运模块，模拟了2020年3月2日至3月17日七里海潟湖在真实条件下的水沙动力过程，以下选取典型流场、波浪场以及模拟结束时刻床层变化作简要分析。

根据图2可知，由于西南部分区域存在围堰养殖区，所以该部分水体不参与水体流通。潟湖实际区域内水流流速有限，潮汐汊道作为连通外海和潟湖的唯一通道，水流集中，所以潮汐汊道内流速较高。受径流下泄影响，落潮作用得以加强，所以在潮汐汊道内落潮流速高于涨潮流速。另外，新开口潮汐汊道入海口门处建有双导堤（图1b），且均向海延伸至地形高程 -2.5 m处。从涨潮、落潮流场分布可知，双导堤对沿岸流起到了阻滞作用，所以导堤外侧流速极小，而内侧水流受导堤束窄流速较高。此外，有效波高分布有明显的向岸衰减趋势，口门处最大有效波高仅为0.18 m，受新开口潮汐汊道尺度限制，波浪进入潮汐汊道后波高迅速衰减，而潟湖内部几乎不受波浪影响。由模拟结束时的地形变化可知，新开口潮汐汊道在真实条件下主要以侵蚀为主，尤其在两端口门处。潮汐汊道入海口门处双导堤外侧有泥沙落淤，而内侧则以侵蚀为主，符合流场分布特征，说明双导堤束窄水流、阻滞泥沙效果显著，其工程效应同新开河港外双导堤类似［13］。潮汐汊道入湖口门受先前建闸影响，断面缩减，流速加剧，泥沙侵蚀明显。潟湖内部虽有淤积，但淤积量极少。

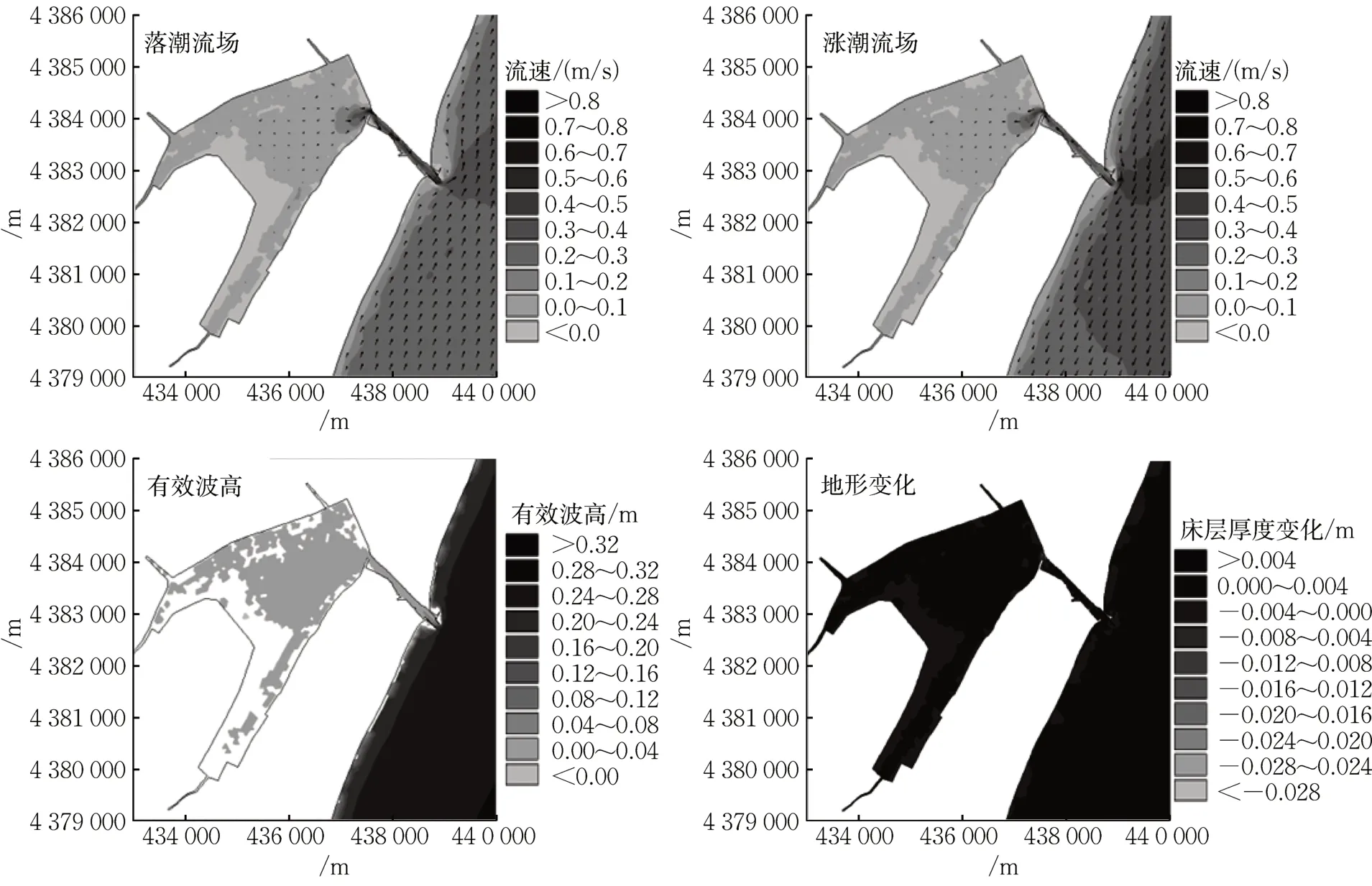
图2 潟湖实际水沙动力过程（2020-03-02—2020-03-17）Fig.2 Hydrodynamics and sediment transport in Qilihai Lagoon under real-world conditions(2020.03.02—2020.03.17)

根据真实条件下的水沙动力过程，对实际模型进行如下3点概化。首先，为减少围堰养殖区域以及局部地形对地貌稳定性研究的影响，基于2018年通过卫星遥感采集得到的岸线数据（图1b），以各部分实测均值作为七里海潟湖尺度，其中新开口潮汐汊道平直，长度为1 800 m，宽度为150 m，四条河流平直且尺度均一，长度为1 000 m，宽度为50 m。以潮汐汊道垂直方向设置潟湖长度为2 000 m，并以潮汐汊道平行方向设置潟湖宽度为1 00 0 m。在所设理想模型区域内布设704 4个三角形网格，共387 0个网格节点，网格尺度为10～30 m（图3）。

其次，七里海潟湖床面表层泥沙的粒径范围为0.002 45～0.314 mm，且其中悬移质（粒径小于0.063 mm）占比62%，中值粒径为0.009 5 mm，推移质占比38%。由于潮汐汊道口门处双导堤阻滞了沿岸输沙，而且受潮汐汊道尺度影响，潟湖内部波浪作用微弱，所以湖内以潮流输沙为主导。此外，潟湖内部水动力较弱，推移质泥沙起动较为困难，因此，设置理想模型底床条件时忽略推移质。由于径流下泄的作用，潟湖内落潮流流速更高，所以涨潮流所携泥沙绝大部分可随落潮流输出，基于七里海潟湖冲淤平衡的特点，为充分考虑潟湖系统内部泥沙冲淤变化，忽略风和泥沙输入的影响，在上游径流边界和潮汐汊道口门边界设置含沙量为0。除模型概化部分，理想模型其余参数均依据实测均值设置，以作为长时间尺度地貌演变模拟的基础。

2.2 参数设置

初始地形采用潟湖实测平均高程-0.5 m，潟湖内部初始流速设为0，湖内含沙量设为实测均值0.01 kg·m-3，理想模型曼宁数设为60 m1/3·s-1，床层厚度为10 m。外海开边界采用新开口潮位站（岸基站）2017年所测得的中等潮差下潮位过程控制，理想模型初始水位采用平均潮位0 m（图4）。地貌加速因子设为100。为考虑临界侵蚀应力、临界淤积应力、泥沙沉速、初始床面高程和径流量对七里海潟湖地貌稳定的影响，研究采用控制单一变量的方法。当对某一参数单独研究时，其他相关参数以实测均值设置，相关参数的赋值如表1所示。七里海潟湖生态修复工程涉及清淤疏浚、退养还湖、岸线修复、汊道改造、植被育养等措施［27，29］。工程导致潟湖系统内部的泥沙粒径级配、底床高程等的变化，所以将表1所示各变量的取值范围以实测均值为基准适当扩大一定范围进行比较分析。由于七里海潟湖水系均为受降雨影响的季节性河流，因此在综合考虑全球气候变化下降雨不确定性和多年平均径流量的基础上，将模拟的径流量最大值设置为10 m3·s-1。

表1 参数条件设置Tab.1 Parameters setting for simulations

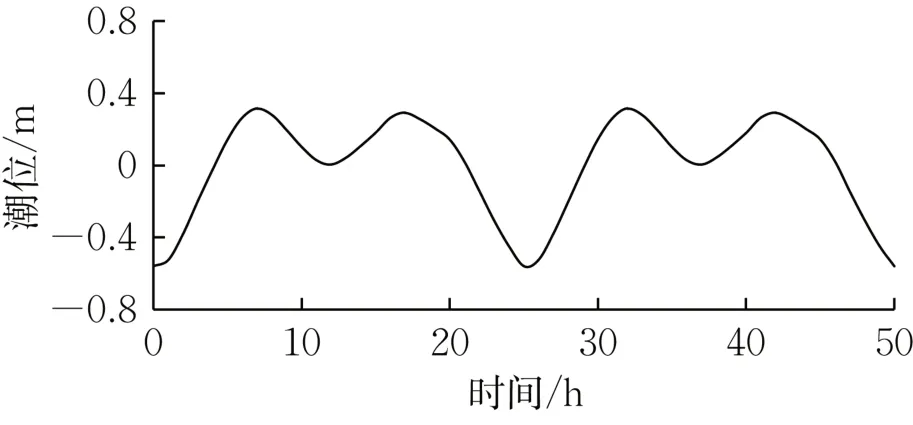
图4 2017年新开口潮位站中等潮差情况下潮位过程Fig.4 Tidal level with medium tidal range collected in Xinkaikou Station in 2017

2.3 泥沙输运

理想模型泥沙输运是基于水动力模块的二维对流扩散方程计算得到的，关于水动力模块的相关计算原理已在之前的研究中进行介绍［28］，以下着重介绍泥沙输运的相关计算方法。泥沙模块基本方程，即深度平均的对流扩散方程如下：

式中：c为垂向平均悬沙浓度；u，v为垂向平均流速；Dx，Dy为水平扩散系数；h为水深；QL为单位水平面积的源流量；CL为源流量的悬沙浓度；S为净冲淤项。其中水平扩散系数在泥沙输运计算中常取为涡黏系数［21］，净冲淤项S通过下式计算得

式中：SE和SD分别为侵蚀项和淤积项，若净冲淤项S为负则表示区域内泥沙侵蚀，若净冲淤项S为正则表示区域内泥沙淤积。由于潟湖系统内以悬移质泥沙为主，而由外海输入的粗颗粒泥沙随涨潮流在潮汐汊道沿程落淤。为进一步简化理想模型，本研究不考虑推移质泥沙输运，当床面切应力大于临界侵蚀应力则悬移质泥沙起动，采用Partheniades公式［32］计算侵蚀项SE，得

式中：E为床面侵蚀度，可取经验值10-4kg·m-2·s-1；τb为床面切应力；τce为临界侵蚀应力。若床面切应力小于临界淤积应力，则悬移质泥沙沉降，采用Krone公式［33］计算淤积项SD

式中：ωs为泥沙沉速；τcd为临界淤积应力；c为含沙量。床面切应力τb由二次摩擦定律计算得到

式中：τbx和τby分别表示x和y方向的床面切应力，ρ0表示流体密度，cb表示摩阻系数，U表示流速。其中摩阻系数cb可由重力加速度g，曼宁数M以及水深h计算得到。

3 结果分析

根据前期真实条件下理想模型地貌演变的模拟［23］，若潟湖系统泥沙净冲淤量的变化量小于最后时刻净冲淤量的0.5%［24］，则认为潟湖系统地貌达到相对稳定。结果表明真实条件下理想模型地貌演变在模拟50年后基本达到稳定。由于当前研究对理想模型进一步概化，较真实情况忽略了泥沙输入等影响，为确保理想模型地貌达到稳定，所以将模拟时间设置为100年，认为模拟结束时刻各参数条件下理想模型地貌均达到稳定。提取该时刻所对应纳潮量、潮汐汊道过水断面最大流量和断面面积，分别利用P-A关系和Qm-A关系构建相互关系以拟合得到地貌稳定性的表示方程，并分析讨论相关影响机制。

3.1 地貌演变结果

模拟各参数条件下理想模型的地貌演变，得到100年后的地貌形态，以下选取5个典型情况下的模拟结果进行展示（图5），详细的地貌演变过程及潟湖水沙动力响应特征可查前期相关研究［23-24，34］。在不同参数影响下，虽然理想模型达到稳定时的最终地貌形态不同，但是潮汐汊道基本处于侵蚀状态。而潟湖内部除了潮沟系统发育的区域，大部分区域处于淤积状态，说明潮汐汊道和潟湖稳定性的影响因素存在差异。此外，发现初始床面高程变化所引起的潟湖内部泥沙淤积较其他参数的作用更大，推测其同潟湖稳定性更为相关。径流量增大导致潟湖系统泥沙淤积量锐减，推测径流量增加对潮汐汊道和潟湖稳定性都会产生一定影响。相关参数对潟湖和潮汐汊道稳定性的影响稍后将通过定量方法详细分析，基于各模拟结果，选取结束时刻的纳潮量P、潮汐汊道过水断面最大流量Qm和断面面积A，构建地貌稳定性的参数表达式。

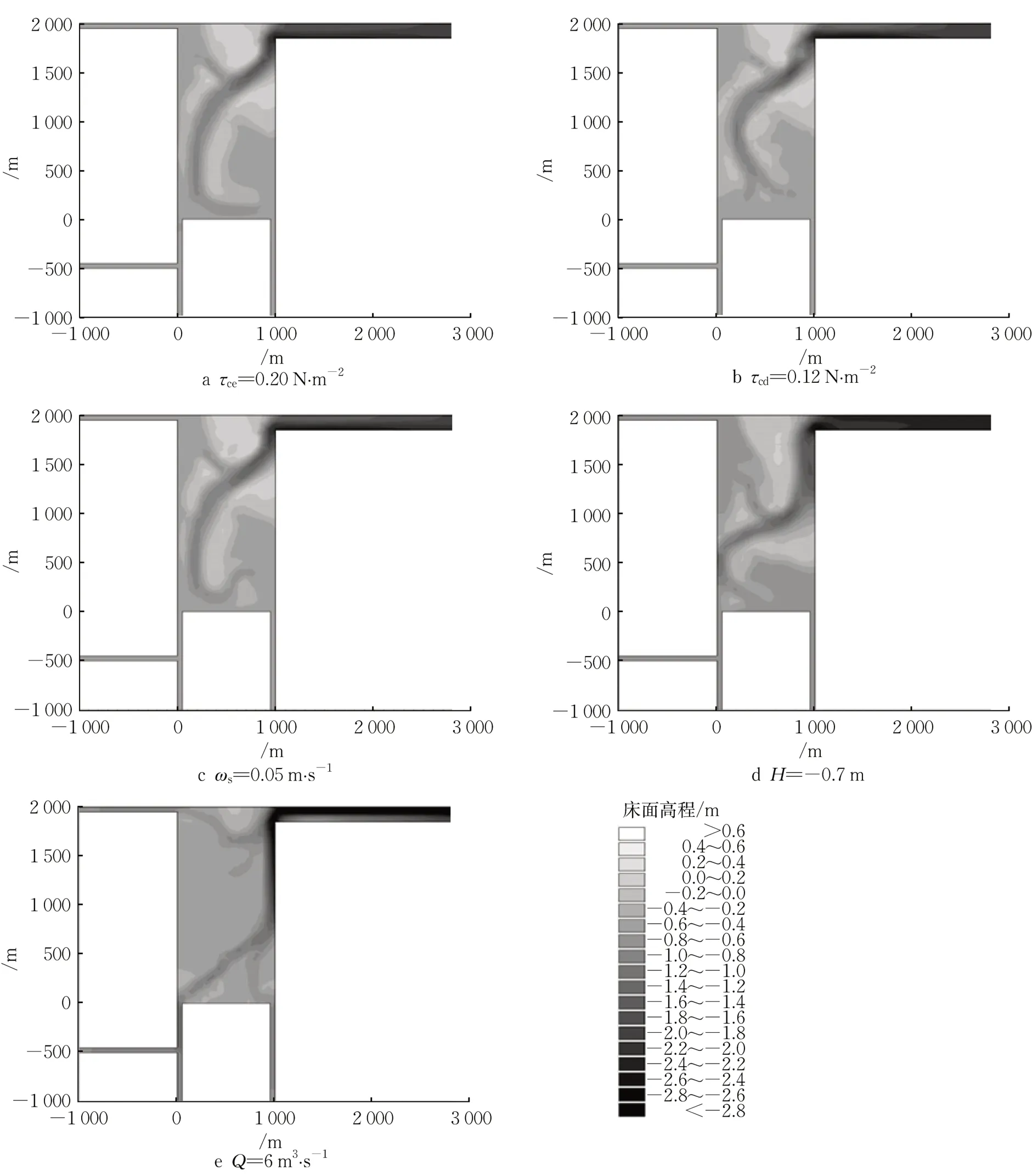
图5 典型参数条件下理想模型的模拟结果Fig.5 The simulation results of the ideal model under typical parameters

3.2 地貌稳定性判定

根据P-A关系表达式［9］

式中：α和β为经验参数，通过数值模拟计算结果拟合（图6a），构建A和P的乘幂关系。从图6a所示的拟合结果看，拟合线确定系数R2为0.43，P-A关系表达式对于计算结果的拟合效果一般。分析发现在径流量较大的情况下，对应点的离散程度也较大。考虑到P-A关系主要针对由潮流作用主导的潟湖，所以去除径流量大于1 m3·s-1所对应的点，并重新拟合以建立P-A关系如图6b所示。经过修正后得到的拟合线确定系数R2提升至0.49，较用全部原始数据拟合的效果更好，据此得到关于七里海潟湖模型的P-A关系表示如下：

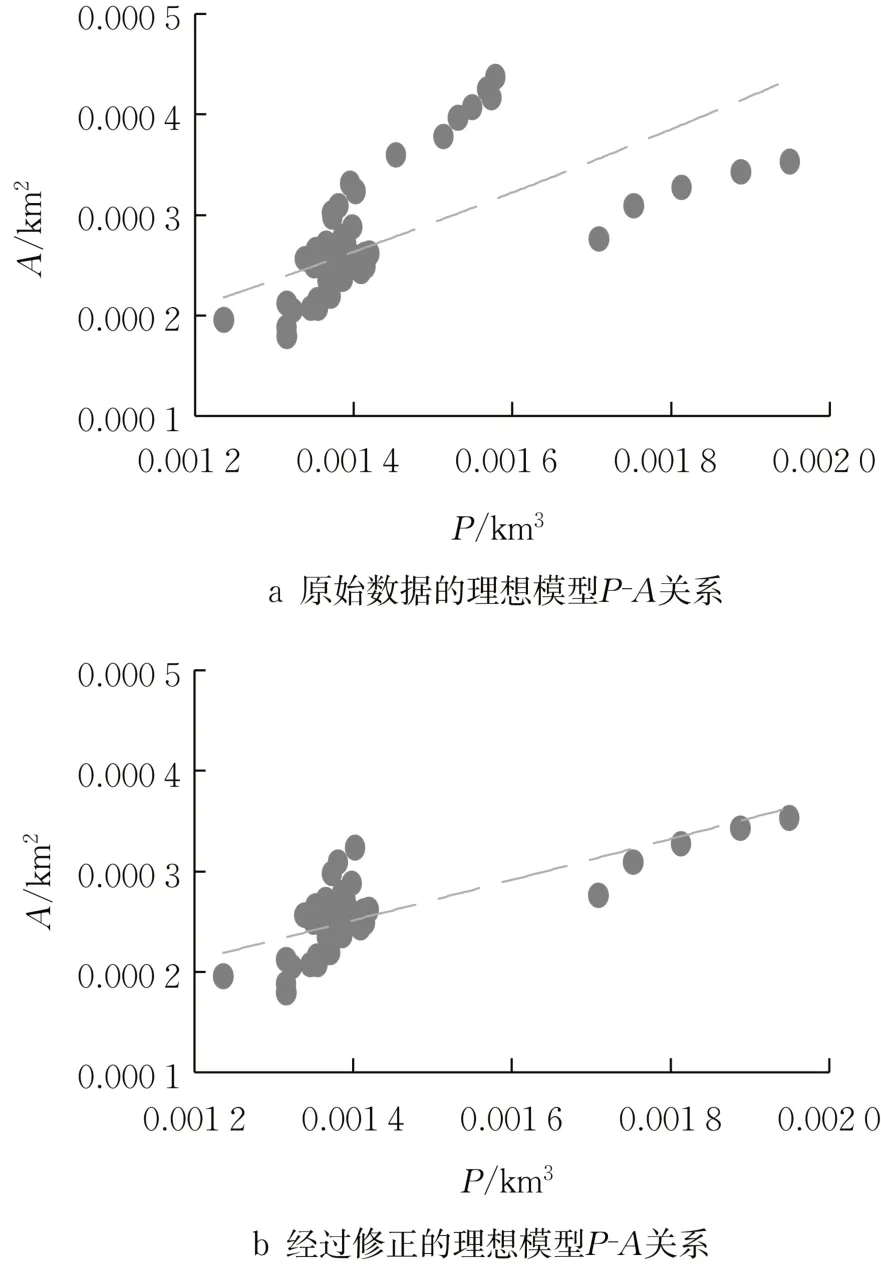
图6 七里海潟湖理想模型P-A关系Fig.6 The P-A relationship of the ideal model of Qilihai Lagoon

如作线性拟合，则可得到P-A关系线性表达式形式：

可见七里海潟湖P-A关系相关性一般。张忍顺［13］在研究新开河港潮汐汊道P-A关系时同样遇到了此类问题，由于新开河港在口门处建有双导堤，且航道经过疏浚，所以维持其口门过水断面面积的纳潮量较小。同样地，七里海潟湖潮汐汊道入湖口门受先前建闸影响，断面缩窄，水流集中而入海口门处也建有双导堤，且汊道内部亦经疏浚。不仅如此，由于径流作用，潮汐汊道内落潮流占优，下泄流量对塑造潮汐汊道稳定断面同样具有决定性作用。因此，需将流量因素加以考虑，并重新构建地貌稳定性表达式。

于是，尝试采用Qm-A关系［16-17］重新构建潟湖地貌稳定性的表达式，根据

式中：τr为参考床面切应力；ub为底部最大流速；n为曼宁系数；hR为水力半径。当地貌达到相对稳定时，参考床面切应力τr约等于1.15倍的临界侵蚀应力τce［35-36］，所以Qm-A关系可改写为

式（15）假定地貌达到稳定前处于侵蚀状态，演变过程中潮汐汊道断面面积逐渐增大，而断面平均流速减小。在一个潮周期内，当潮汐汊道口门处达到最大流量，床面切应力即达到最大值，此时若床面切应力τb等于参考值τr，则可维持潮汐汊道泥沙净输运量不变，即地貌演变达到相对稳定的状态。式（15）中水力半径hR同断面面积A和湿周hR有关，但是考虑到hR1/6的值对Qm-A关系影响有限，所以将Qm-A关系近似看作线性关系。选取各参数条件下模拟的100年中最后一个潮周期计算所得的潮汐汊道口门处断面最大流量Qm和断面面积A进行线性拟合，得到结果如图7所示。通过全部原始数据线性拟合所得到的拟合线确定系数R2为0.93，说明Qm和A具有很强的线性关系，且以线性的Qm-A关系表征的地貌稳定性较P-A关系的可靠度更高。根据式（15），临界侵蚀应力的变化会对Qm-A关系产生影响，故将临界侵蚀应力变化情况下的散点去除并进行重新拟合，所得到的拟合线确定系数R2为0.98（图8）。根据前面P-A关系修正途径进行比较分析，发现Qm-A关系更适用于判定浅水情况以及径流汇入量较小情况下的潟湖潮汐汊道稳定性判定。至此，可以得到Qm-A关系如下：

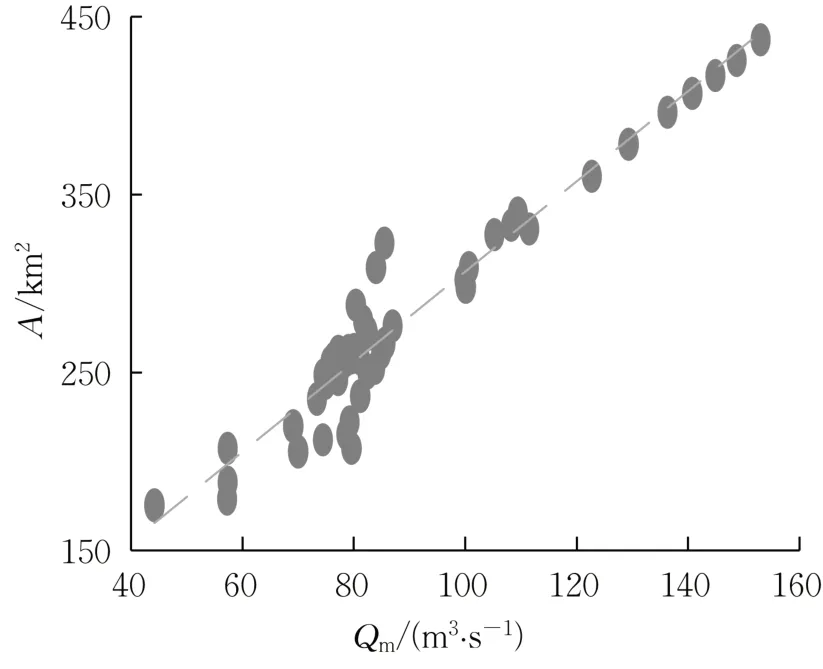
图7 七里海潟湖理想模型Qm-A关系Fig.7 The Qm-A relationship of the ideal model of Qilihai Lagoon

图8 经过修正的七里海潟湖理想模型Qm-A关系Fig.8 The revised Qm-Arelationship of the ideal model of Qilihai Lagoon

在现场观测和物理模型试验中发现，实际最大流量与理论最大流量的误差范围在20%［35］，上式基于线性Qm-A关系，所以在利用式（16）判定潟湖稳定性时将误差范围确定为20%，即当实时最大流量同利用Qm-A关系计算得到的最大流量Qm的差值稳定保持在20%以内则认为潮汐汊道已经达到稳定。

3.3 地貌稳定性分析

由于模型忽略了泥沙输入，所以泥沙净冲淤量保持稳定时，潟湖系统则达到相对稳定状态。选取模拟结束时刻的泥沙净冲淤量为参考标准，若从任一时刻开始潟湖系统泥沙净冲淤量的变化量小于最后时刻净冲淤量的0.5%［24］，则认定从该时刻开始潟湖达到相对稳定状态。分别采用上述得到的Qm-A关系和净淤积量变化量对各参数条件下潟湖理想模型达到相对稳定的时间进行计算得到表2。

对比两种不同方法所判定的潮汐汊道达到相对稳定的时间发现，以Qm-A关系计算的时间少于以泥沙净冲淤量变化量所计算得到的时间。潟湖达到相对稳定的时间明显高于潮汐汊道达到相对稳定的时间。以下针对各参数条件对潟湖系统稳定性影响详细讨论。临界侵蚀应力较小（τce＜ 0.16 N·m-2），泥沙更易起动，所以地貌达到相对稳定的时间更长，而且潮汐汊道对其变化更为敏感。当临界侵蚀应力增大（τce＞ 0.16 N·m-2），潮汐汊道达到相对稳定的时间基本保持不变，但潟湖稳定达到相对稳定的时间大幅减小，此时临界侵蚀应力的变化对潟湖稳定性影响更大。整体来看在不同临界侵蚀应力的条件下，潟湖滞后于潮汐汊道所达到稳定需要的时间随临界侵蚀应力增大而减小。临界淤积应力对潮汐汊道稳定性的影响小于对潟湖稳定性的影响。主要原因是潮汐汊道内以侵蚀为主，而潟湖内部流速较小，除潮沟系统发展区域外，大部分区域以淤积为主，所以临界淤积应力对潟湖影响更大。与临界淤积应力对潟湖的影响机制类似，泥沙沉速对潟湖稳定性的影响极为显著，但对潮汐汊道稳定性影响较小。此外，当初始地形高于最低潮位（-0.56 m），即存在出滩情况时，潟湖系统达到相对稳定的时间较完全淹没情况下的时间长。在完全淹没时，潟湖大致滞后潮汐汊道14年才能够达到稳定状态。在不同径流量条件下，潟湖和潮汐汊道达到稳定的时间均随径流量增大而增大，说明径流变化对潟湖系统的影响相对一致。潟湖的侵蚀一般由落潮流主导，而径流量的增加则加剧了落潮流的侵蚀作用，更多的泥沙被带向外海，潟湖整体处于侵蚀状态，所以导致潟湖和潮汐汊道达到相对稳定的时间均相应延长。

本文所构建Qm-A关系适用于有径流汇入且具有单一潮汐汊道的海岸潟湖地貌稳定性的研究。在该研究基础上，将继续研究有径流汇入的多潮汐汊道的海岸潟湖地貌稳定性，此类沙坝-潟湖海岸系统的水沙动力作用更为复杂。虽然先前的研究表明多潮汐汊道系统难以达到稳定状态，甚至存在潮汐汊道淤塞的风险［37-38］，但考虑到七里海潟湖目前工程维护的状况以及径流汇入的条件，其动力条件或能够维持多潮汐汊道系统的相对平衡状态。根据七里海潟湖潮沟系统的发育阶段可知［24］，径流入湖河口和潮汐汊道入湖口门的相对位置对地貌演变过程存在一定影响，所以潮汐汊道的布置方式同样值得探究。此外，在沿岸输沙和波浪掀沙的共同作用下，潮汐汊道的稳定性同沙坝地貌稳定性直接相关，研究将侧重于潟湖动力作用组合及多源泥沙输入的影响。同时，利用MIKE21模拟长时间尺度的地貌演变难以精确考量短时间尺度的动力作用，例如风暴潮、洪水、人类活动等，因此后续研究也将考虑此类过程性事件对地貌稳定性的影响。

4 结论

基于七里海潟湖相关资料，建立了单一潮汐汊道的海岸潟湖理想模型，针对临界侵蚀应力、临界淤积应力、泥沙沉速、初始床面高程和径流量，模拟了理想模型在各项参数条件下100年的地貌演变过程，通过提取模拟结束时刻的相关参数，建立了能够用以判定潮汐汊道稳定性的关系表达式，分别为P-A关系（A=0.374 9P1.112）和Qm-A关系（A=2.53Qm+53.34），通过比较拟合线确定系数发现Qm-A关系更适用于浅水情况和径流量汇入较小情况下单一潮汐汊道的海岸潟湖的稳定性判定。基于Qm-A关系表达式和泥沙净冲淤量变化量分别计算了理想模型潮汐汊道和潟湖达到相对稳定的时间，通过比较发现，由Qm-A关系计算的稳定所需时间更短，且潟湖较潮汐汊道的稳定存在明显的滞后。分析各项参数对稳定性的影响发现，由于潮汐汊道受侵蚀作用为主，而潟湖受淤积影响较大，因此临界侵蚀应力的变化对潮汐汊道稳定性的影响更大，临界淤积应力、泥沙沉速和初始地形的变化则对潟湖稳定性的影响更为显著。此外，上游径流量的增加会加剧潟湖落潮流的侵蚀作用，所以其对潟湖和潮汐汊道稳定性的影响基本一致。

作者贡献声明：

匡翠萍：项目及基金负责人，研究方法及模拟方案，论文撰写与修改；

范家栋：数值模拟，数据分析，论文撰写；

董智超：数值模拟，数据分析；

韩雪健：数据分析。