软土地区盾构侧穿SF油罐扰动控制数值分析

文明， 郭静， 景浩， 包晓红， 柳献

（1. 同济大学土木工程学院，上海 200092；2. 宁波市市域铁路投资发展有限公司，浙江 宁波 315000；3. 镇海石化工程股份有限公司，浙江 宁波 315000；4. 宁波市轨道交通集团有限公司建设分公司，浙江 宁波 315000）

盾构隧道掘进中由于开挖引起地层损失，盾构与土体相互作用引起地下构筑物受力环境发生变化。盾构施工对地下构筑物影响研究，理论分析方面，张琼芳等［1］基于Mindlin解计算出盾构施工对已建隧道附加应力，应用Winkler地基梁理论得出隧道变形量；甘晓露等［2］采用Pasternak弹性地基梁模型和Loganathan-Polous解，提出隧道下穿已建隧道纵向变形简化计算方法；冯国辉等［3］将管线简化成Euler-Bernoulli梁搁置于Kerr地基模型上，利用差分法得到盾构掘进引起上覆管线竖向位移解。数值分析方面，刘维正等［4］建立盾构下穿铁路框架桥数值模型，研究不同工况下框架桥和轨道的变形受力特性；丰土根等［5］针对盾构隧道侧穿桥梁桩基工程，进行数值模拟研究加固前后地表沉降、桩基附加力及位移情况；沈俊等［6］通过数值模拟分析叠线盾构下穿并行燃气管线引起管线的变形与受力特征。

对于地下储油罐等敏感地下构筑物，盾构掘进施工期间若扰动过大，易造成油管拉裂，卸油口及检修人孔局部受损致使泥土进入，严重时会出现油品渗漏等事故，施工前应对油罐受扰动情况进行预测分析。康永胜［7］结合工程实例利用ANSYS对地面和油罐沉降进行计算；师宏耀［8］运用peck沉降公式针对隧道与油罐距离差异分析油罐沉降规律；胡磊等［9］采用peck经验公式结合数值模拟方法给出油罐变形数据。盾构掘进过程中破坏地层初始应力场，造成应力重分布，同时材料的应力应变表现为非线性。为全面研究罐体的受扰动状态，考虑各项控制因素影响，解析法无法处理存在一系列自变量的复杂工况，仅能采用数值分析方法。有限元分析作为数值分析方法的一种，其将土体及构件离散成通过节点连接的有限数量的单元，将荷载及边界条件等效加载在单元上，利用应力应变关联的本构关系，将平衡方程转化为线型方程组求解。

本文以宁波市轨道交通3号线二期盾构区间侧穿某加油站罐区工程为背景，考虑油罐材料参数影响，分析扰动主要控制因素，采用数值分析方法得出各工况下油罐变形及应力值，得出优化组合工况后分析油罐受扰动引起变形及应力分布情况，并提出施工期间应急控制措施。

1 工程概况

本工程盾构机采用小松土压平衡圆形盾构机，主机长9.055m，平均掘进速度12m·d-1。管片内径5.5m，外径6.2m，环宽1.2m，采用通用楔形环错缝拼装。本工程平面及立面布置图如图1所示。

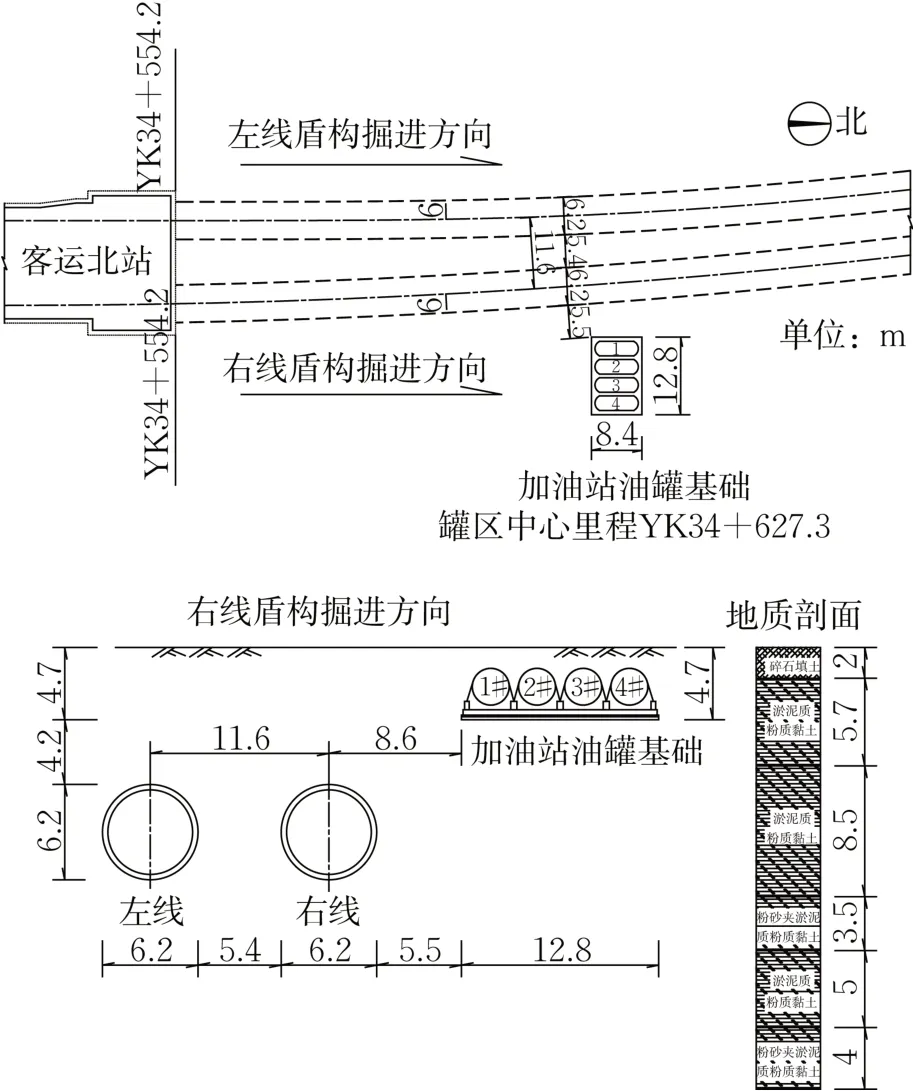
图1 隧道与油罐区平面及立面布置图（单位：m）Fig.1 Plan and Elevation Layout of Tunnel and Oil Tank Farm (Unit: m)

埋地罐区设置30m3油罐各4只，罐体采用埋地钢-玻璃纤维增强塑料双层油罐（SF型）。油罐区垫层及回填情况如图2所示。

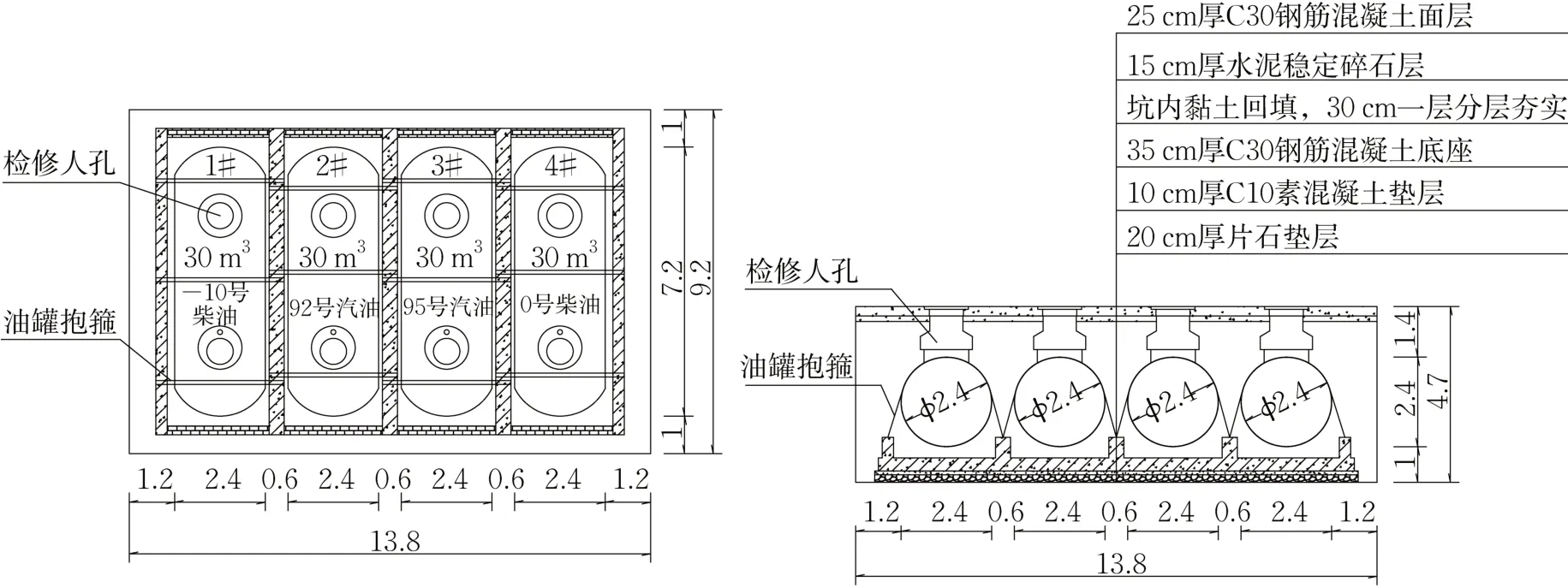
图2 油罐区布置平面及剖面（单位：m）Fig.2 Layout Plan and Section of Oil Tank Farm (Unit: m)

场地土层构成依次为为①1b碎石填土、①3淤泥质粉质黏土、②2淤泥质粉质黏土、③1粉砂夹淤泥质粉质黏土、④1淤泥质粉质黏土、④1a粉砂夹淤泥质粉质黏土、④1淤泥质粉质黏土等。

2 扰动主要控制因素

盾构掘进对地下构筑物的扰动因素，主要有开挖引起的地层损失、盾构与土体相互作用荷载、注浆压力及注浆材料性能等。

2.1 地层损失

地层损失是开挖土体体积与建成隧道体积（含隧道周边同步注浆土体体积）之差，常用地层损失率来分析盾构施工对地层扰动特征。地层损失率是指单位土体损失体积与理论开挖土体体积的比值。根据地面沉降实测数据，经Peck公式反推导可得到地层损失率取值。宁波软土地区地层损失率约为0.5%～2%，平均值1%。根据地层损失率的不同，本文取4组工况分析如表1所示。

表1 地层损失率工况Tab.1 Working conditions of formation loss rate

2.2 盾构与土体作用荷载

盾构与土体相互作用荷载主要有盾构掘进正面附加推力、千斤顶推力引起的盾壳与土体的摩擦力、盾构刀盘扭矩引起的刀盘正面及侧面与土体的摩擦力、同步注浆压力等。根据梁荣柱等［10］提出的盾构掘进正面附加推力计算公式，该值主要与盾构掘进速度、刀盘转速相关。根据宁波地区施工经验，穿越敏感构筑物采取的控制变形措施，掘进速度宜控制在20～40mm·min-1，刀盘转速宜控制在0.9～1.2r·min-1。根据各取值组合取4组工况分析如表2所示。

表2 正面附加推力工况Tab.2 Frontal additional thrust conditions

来弘鹏等［11］根据盾构周边土压力分布实际情况，改进摩擦力计算公式并提出盾壳与周边土体的摩擦力表现为上部小、下部大且不均匀分布特点。摩擦力大小与周边土体内摩擦角及容重、隧道埋深具有相关性。考虑模型输入条件进行简化处理，盾壳上部及下部摩擦力取平均值，上部盾壳与土体摩擦力取53KPa，下部盾壳与土体摩擦力取80KPa。

根据武崇福等［12］理论，刀盘正面及圆周与土体之间作用产生的摩擦力矩是盾构施工引起地层横向位移的原因之一。本文不考虑因左线先掘进扰动土体后，右线掘进时造成土体附加应力引起的摩擦力扭矩增大问题［13］，视为双线扭矩数据一致。刀盘正面、侧面与土体摩擦力扭矩可参考钟小春等［14］提出的扭矩计算公式，扭矩数值大小主要与土体容重、隧道埋深、刀盘开口率、刀盘外沿宽度相关，本文中扭矩值取1 073KN·m。

2.3 同步注浆

软土层由于强度指标较低，盾尾从初拼管片脱离后，刀盘超挖形成的土体空隙引起周边土体坍塌至管片上，形成土层松动、土体强度降低等现象，需要通过同步注浆及时填充空隙，避免地层产生较大变形，从而降低对周边地下构筑物的影响。同步注浆主要控制因素有：注浆压力、注浆材料、注浆量、注浆速度及注浆时间等。

根据国内研究表明，注浆压力应与注浆处土体的静止水土压力相当，对于控制地层变形效果最为显著，一般控制在0.2～0.4MPa。若注浆压力过大，会引起劈裂、漏浆，对地层扰动较大，一般不宜超过0.4MPa。根据本工程隧道埋深情况，注浆压力应采用太沙基土压力计算方法较合理，计算得注浆口处注浆压力0.2MPa。为验证注浆压力选取合理性，取4组工况分析如表3所示。

表3 注浆压力工况Tab.3 Grouting pressure conditions

注浆材料按照注浆方式可分为单液浆、双液浆两类。其中单液浆分为可硬性浆液和惰性浆液。目前宁波地区采用的小松盾构机配置单液同步注浆系统。由于可硬性浆液中掺入水泥等可硬性胶凝材料，强度高且收缩率低，较惰性浆液具有良好的材料性能。鉴于浆液长期硬化后弹性模量可达到200～400MPa，施工阶段分析中应取浆液初凝阶段弹性模量。根据单液浆配合比不同引起的材料性能差异，以及考虑浆液龄期对分析结论影响，共取4组工况如表4所示。

表4 单液浆材料工况Tab.4 Working conditions of single slurry materials

3 数值模拟

数值模型建立简化及假定条件如下：

（1）土体为匀质、各向同性的弹塑性材料。

（2）盾构正面附加推力均匀作用于开挖面。

（3）鉴于仅研究局部范围，不考虑线路纵坡、地面及道路荷载的影响。

（4）仅考虑地下水对土体变形影响，不考虑渗流与固结耦合作用、水位高度变化的影响。

（5）仅考虑盾构施工阶段土体变形，不考虑扰动土体固结引起的长期沉降。

（6）盾构按照平均掘进速度掘进，不考虑土体变形的时间效应。

盾尾注浆层采用均质等代层处理，因软土受扰动引起隧道壁位移较大，等代层厚度将大于盾尾空隙［15］，等代层厚度取170mm。等代层弹性模量及注浆压力变化如表5所示。为便于模拟地层损失，采取在同步注浆层外设置一层等厚均匀层，其弹性模量取周边土体的1%［16］。注浆层及土体损失层简化如图3所示。

表5 等代层弹性模量及注浆压力变化表Tab.5 Changes in elastic modulus and grouting pressure of equivalent layers

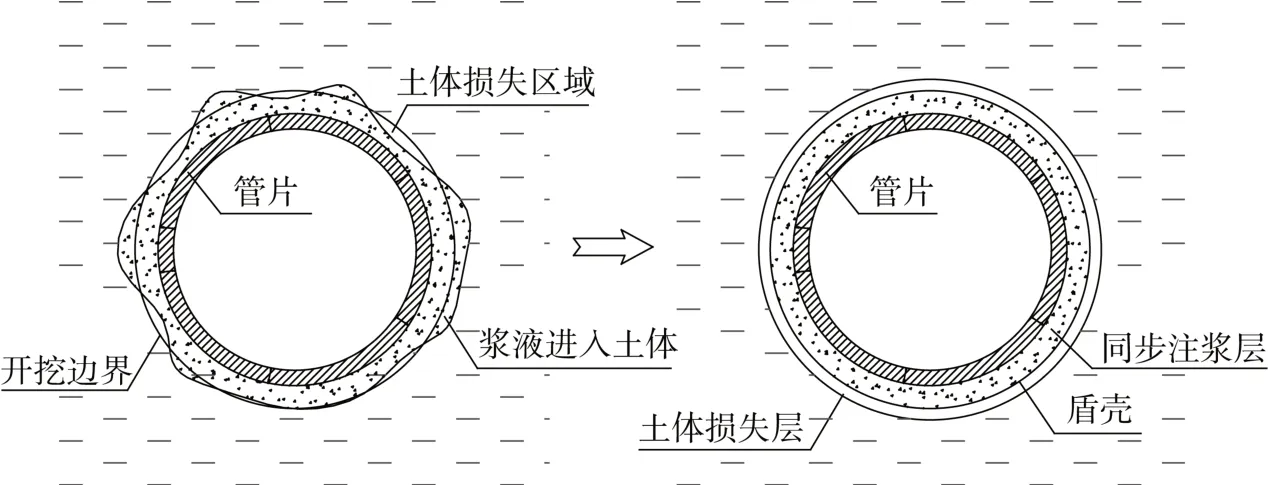
图3 同步注浆层及土体损失层简化模拟Fig.3 Simplified simulation diagram of synchronous grouting layer and soil loss layer

储油罐罐体材质为钢-玻璃纤维增强塑料双层油罐（SF型），其内层罐体采用厚6mmQ235B钢材，外层罐体采用厚4mm玻璃纤维增强塑料（FRP材料）。外层罐体完整包容内层罐体，罐体间形成连续贯通间隙，并设置可靠支撑。油罐结构如图4所示。为便于研究罐体各层受力状态，将内层、外层及间隙分别建立模型［17］，假设各层均为各向同性弹性材料。罐体材料性能如表6所示。

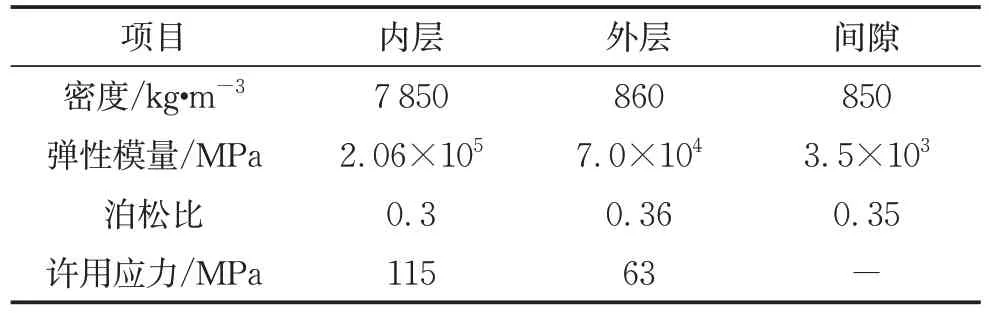
表6 油罐各层材料参数及力学性能表Tab.6 Material parameters and mechanical properties of each layer of oil tank

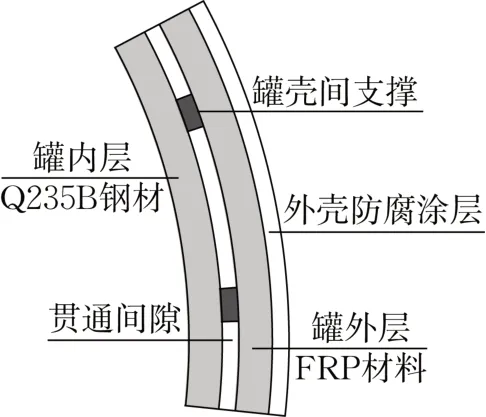
图4 SF双层油罐罐体横剖面图Fig.4 Cross sectional view of SF double-layer oil tank body

盾构开挖面前方土体受扰动，采用开挖面前一环设置应力释放单元，采用降低材料弹性模量方法模拟，模量取周围主体的1%。管片拼装引起的衬砌刚度折减系数0.85。利用MIDAS GTS/NX有限元软件，结合场地土层性质，土层、填土等非线性材料模型采用修正摩尔—库伦（Modified Mohr-Coulomb）弹塑性模型。模型具体参数如表7所示［18］。

表7 修正摩尔-库伦模型参数Tab.7 Revised parameters of the Mohr- Coulomb model

根据数值模拟需求进行室内三轴与固结试验，得到模型参数如表8所示。

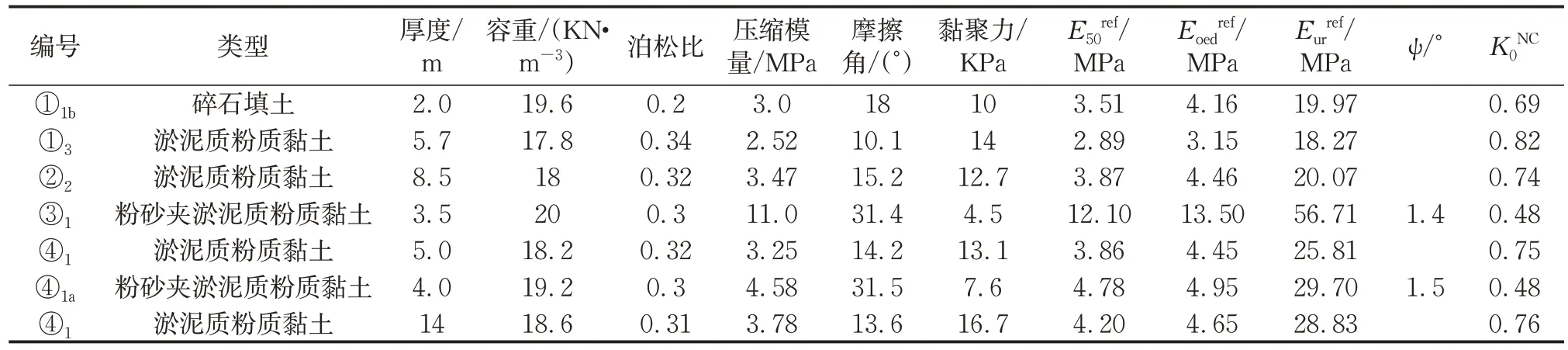
表8 土层主要物理参数表Tab.8 Main physical parameters of soil layer

为消除边界约束对计算结果的影响，模型尺寸选取右线隧道直径5倍范围以外形成的三维实体，模型尺寸为65m×36m×28.7m。建立模型如图5所示。

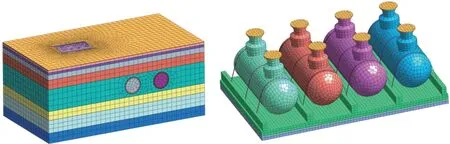
图5 三维实体模型图例Fig.5 Legend of 3D solid model

通过开挖土体、管片、荷载及边界条件激活与钝化实现施工阶段模拟。盾构掘进2环划分为一个施工阶段，共划分42阶段。模型边界内左右线掘进行程均为30环，先掘进左线（1～21阶段），完成后掘进右线（22～42阶段）。主要施工阶段内容见表9。

表9 主要施工阶段内容表Tab.9 Main construction stage content table

4 数值分析

针对土体损失、正面附加推力、注浆压力及注浆材料等各参数取值差异，分析各施工阶段油罐竖向变形及应力变化规律。鉴于组合工况较多，受篇幅所限本章节中数据取值作如下限定：

（1）取4只油罐均位于空载工况下数据。

（2）分析结果取影响较大的1#油罐内壁数据。

（3）取优化工况作为分析的基础工况。

（4）油罐变形取竖向变形数值，受力状态仅取某节点范式等效应力数值。

（5）考虑油罐各部位受干扰敏感性，竖向变形取值为罐底中心位置，等效应力取值为近隧道一侧罐侧壁中心位置。

4.1 土体损失影响

从数值分析数据以及图表曲线趋势可得下列变化规律：

（1）油罐空载工况下竖向变形以隆起为主，变形量受罐区与盾构距离影响显著。左线距离罐区较远，隆起变化趋势较小，受模型边界影响在15阶段出现隆起极值。右线盾构介入后隆起增量变化较大，在28阶段（右线掌子面距离罐区中心最近时）出现隆起极大值；之后随着盾构作用退出，受土体损失影响隆起量急剧减小，且在土体损失率较大工况下出现沉降效应。

（2）左线远离罐区对油罐应力状态干扰相对较小；右线盾构介入后对罐区应力扰动显著增大，在盾构穿越模型区域内出现较大应力增幅，且持续受盾尾同步注浆影响，等效应力最终阶段达到极值。

如图6所示，随着土体损失率取值差异，油罐竖向变形呈现出梯度变化。最终状态下，损失率0.5%隆起量2.3mm，损失率1%隆起量1.6mm，损失率1.5%沉降量0.1mm，损失率2%沉降量1.7mm。土体损失率对于控制隆沉具有显著影响。随着损失率增大，罐侧等效应力值增大，最终阶段下，损失率0.5%等效应力14.9MPa，损失率2%等效应力19.4MPa。同时较大损失率会引起盾构正上方地表沉降较大，为便于施工控制，建议土体损失率取均值1%。

4.2 正面附加推力影响

如图7所示，正面附加推力对油罐变形及受力状态影响较为显著，各项指标均呈现出梯度变化。在28阶段，推力50KPa隆起量2.4mm，推力75KPa隆起量3.2mm，推力100KPa隆起量3.9mm，推力125KPa隆起量4.2mm。油罐应力在右线掘进后增长显著，最终状态下，较小正面附加推力引起较大应力指标，且随着正面附加推力递减，等效应力呈加速递增趋势。同时较小的正面附加推力需采取较低掘进速度，较高刀盘转速，对油罐扰动时间较长，综合比较并结合以往工程实践经验，建议正面附加推力值取100KPa。

4.3 注浆压力影响

如图8所示，同步注浆压力取值对油罐变形及应力影响曲线，与正面附加推力取值影响类似。在最终阶段，较小的注浆压力引起较小的竖向变形，但引起较大的罐壁附加等效应力。最终阶段下，注浆压力0.15MPa隆起量1.3mm，等效应力16MPa，盾构施工引起的附加应力2.9MPa；注浆压力0.3MPa隆起量2.8mm，等效应力14.8MPa，盾构施工引起的附加应力1.7MPa。为避免因注浆压力过大对土体引起过大扰动，注浆压力应取较小值，同时尽量降低施工引起的附加应力，建议注浆压力取0.2MPa。

4.4 注浆材料影响

如图9所示，浆液弹性模量取值对于竖向变形有一定影响，弹性模量较大的浆液，引起较小的竖向变形，较大的等效应力。以28阶段为例，弹性模量10MPa隆起量4.2mm，弹性模量20MPa隆起量3.9mm，弹性模量40MPa隆起量3.6mm，弹性模量100MPa隆起量3.2mm。同时较大的弹性模量引起较大的附加应力，最终阶段下，弹性模量10MPa盾构施工引起的附加应力2.2MPa，弹性模量100MPa盾构施工引起的附加应力3.3MPa。分析模型上可以得出，注浆材料强度主要影响盾构正上方地表变形，综合考虑变形与产生的附加应力影响，结合宁波地区盾构实施经验，建议浆液弹性模量取0.2MPa。

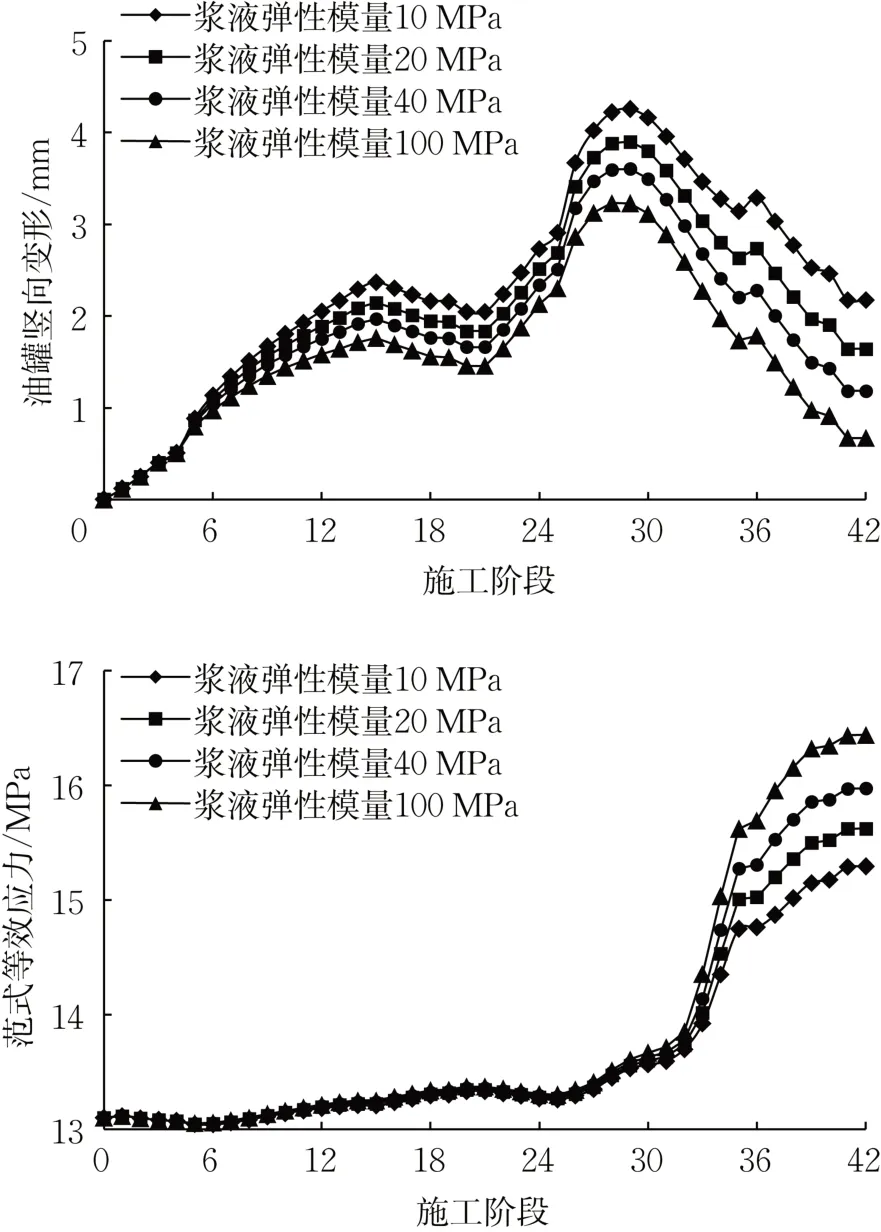
图9 注浆材料工况下竖向变形及等效应力趋势Fig.9 Vertical deformation and equivalent stress trend of grouting material under working conditions

5 分析结果

根据上述图表趋势，考虑参数取值不同进行组合计算，得到优化工况见表10。

表10 优化工况组合Tab.10 Optimization condition combination

所有油罐空载、优化工况下最终阶段竖向变形及等效应力云图分布如图10～图11所示。

从云图数据可以得到下述变化规律：

（1）油罐变形状态与隧道距离密切相关。左线掘进中罐区整体呈现沉降状态，右线掘进中罐区以隆起状态为主，且距离隧道较近油罐出现范围较广的隆起区域，主要位于罐底及大里程端封头。掌子面通过罐区后均出现一定程度的沉降效应，其中罐区中心扰动较大，中心油罐较外围油罐出现较大沉降量。

（2）油罐内壁等效应力值远大于外壁，罐体承载以内层钢罐体受力为主。油罐应力状态与隧道距离密切相关，距离隧道较近区域出现较大附加应力，且罐区中心因扰动较大，中心油罐较外侧油罐出现较大附加应力。

优化工况下出现极值时各油罐变形及等效应力数值如表11所示。

表11 罐区变形及应力极值统计表Tab.11 Statistical table of tank farm deformation and stress extreme values

6 监测数据分析

客运北站至镇海大道站区间左线隧道于2022年6月30日始发，2022年7月12日穿越罐区；右线于2022年7月30日始发，2022年8月13日穿越罐区。罐区范围内四周边角设置4个沉降监测点，编号JC1-1～JC1-4。监测布点平面如图12所示。

图12 监测布点平面图Fig.12 Monitoring point layout plan

以影响较大的右线掘进数据为例，针对监测数据与数值分析结果作对比。为接近实际情况，数值模型取4只油罐按3/4满载油量工况。在模型范围内共计掘进30环，对应于8月9日至8月14日监测数据，根据每日掘进环数取对应地表竖向变形数据。

由图13可知，各监测点实测数据与模型数据总体隆沉变化趋势一致。盾构掘进通过罐区后，JC1-1测点实测数据0.4mm，模型数据0.6mm；JC1-3测点实测数据2.3mm，模型数据1.8mm，模型变形量与实测数据较为接近。地表最大沉降量2.8mm，最大隆起量2.1mm，最大变形速率1.0mm·d-1，均满足监测变形要求。因模型数据未考虑盾构掘进过程中的时空效应，未考虑每日掘进进程的差异，同时监测数据存在一定的初始变形量等原因，引起实测变形量与模拟数值存在一定差异。

图13 油罐周边监测点竖向变形时程曲线（2022年）Fig.13 Vertical deformation time history curve of monitoring points around oil tanks（2022）

7 结论

（1）土体损失率、正面附加推力、注浆压力、注浆材料在合理取值区间时，各项数值差异对油罐变形及应力影响的趋势呈现两级分化状态；对油罐采取变形及应力指标双控，选取合理参数可作为油罐扰动控制方法。

（2）罐区变形以竖向为主，空载工况下整体呈现隆起效应；满载工况下经历整体沉降、底部及封头隆起、整体沉降三阶段。距离隧道较近的油罐呈现较大隆起量，中心油罐较外侧油罐呈现较大沉降量。

（3）油罐产生的附加应力值与盾构距离密切相关，距离盾构较近区域出现较大附加应力。油罐各项应力极值均小于罐体材料许用应力，以内层钢罐体受力为主。

（4）油罐满载工况下，变形及附加应力值均低于空载工况。类似项目中若变形数据接近预警值时，可采取油罐内排空燃油后用清水注满作为应急处理措施。

（5）盾构掘进期间采取优化工况后，现场监测数据时程变化趋势与数值分析数据一致，变形量及变形速率均满足监测要求，数值分析方法及扰动控制措施均得到了合理性验证。

作者贡献声明：

文 明：数值分析，数据处理，论文编撰；

郭 静：罐体结构技术支持，参与数值分析；

景 浩：盾构掘进技术支持，论文校审；

包晓红：论文研究思路指导，论文校审；

柳 献：提供技术支持和指导意见。