卫星长期集群飞行的稳定性与灵活性分析

周 亮，户 鲲，杨益嘉，罗建军

（1.中国航天科工集团智能科技研究院有限公司，北京，100043；2.航天防务智能系统与技术科研重点实验室，北京，100043；3.中国运载火箭技术研究院，北京，100076；4.中国航空规划设计研究总院有限公司，北京，100120；5.西北工业大学航天学院，西安，710072）

0 引 言

随着卫星小型化和模块化技术的发展，具有资源共享和信息传递能力的集群飞行卫星［1-2］，相比于传统的单一的卫星，快速性和灵活性等优势越来越凸显。欧洲航天局的PRⅠSMA 任务［3-4］、以色列理工大学的SAMSON 计划［5］、德国维尔茨堡大学Netsat 项目［6］、英国的BAE 系统［7］，以及美国国防部高级研究计划局（Defense Advanced Research Projects Agency，DARPA）的F6 系统［8］（由于经费等问题，该项目已停止，其关键技术转移到凤凰计划等项目中）是卫星集群飞行的典型演示验证项目。

卫星集群飞行对精确的几何构型没有特定的要求，而是通过位置保持控制和重构机动来维持一种松散的集群结构，同时保证燃料消耗较少。本文针对卫星长期集群飞行任务，提出了一种使用相对轨道要素（Relative Orbital Elements，ROEs）描述的集群稳定性与灵活性的分析方法，相对于动力学描述的卫星集群相对运动具有几何关系明确、便于分析等特点。

1 相对轨道要素表示的集群飞行

1.1 相对轨道要素与相对运动

相对轨道要素由相对偏心率矢量（Eccentricity，e矢量）和相对倾角矢量（Ⅰnclination，Ⅰ矢量）组成［2-3，6］。偏心率矢量e可表示为

式中ω为轨道六要素中的近地点幅角。

两卫星的相对偏心率矢量Δe可定义为

式中φ为该矢量的相位角；δe为该矢量的模值。

相对倾角矢量Δi可定义为

式中δi为两轨道平面夹角；θ为卫星S2穿过卫星S1的轨道平面时S1的纬度幅角，其正方向为相对于升交点的上升方向。

对于倾角i与升交点赤经Ω均相差较小的情况，式（3）可以简化为

两卫星的相对位置矢量Δr在轨道坐标系Oxyz中的径向（R向）、切向（T向）和法向（N向）分量可以近似表示为

式中a为轨道半长轴，Δa=a2-a1；u为平纬度幅角；u0为平纬度幅角的初值，Δu=u2-u1；Δl表示u的变化带来的切向位置漂移，Δl≈Δu+ cosi⋅ΔΩ。

由式（5）可得，使用相对轨道要素表示的卫星相对运动方程如下：

式中v为半径为a的圆轨道上的卫星速度大小。Δa和Δu影响很小，可忽略。使用相对轨道要素表示的相对运动方程可以简化为

S2与S1的相对运动在参考轨道面内为椭圆。其半长轴为2aδe，沿T向；半短轴为aδe，沿N向。由上可知，使用相对轨道要素描述的卫星相对运动，可以通过较少的轨道要素，表述明确的几何关系，从而简化集群的构型设计。

1.2 集群的被动安全

集群中的卫星在任务期间，不与其他卫星产生碰撞，可定义为集群的被动安全［3］。

根据轨道力学和轨道中常见的干扰因素，卫星相对运动的不确定性主要集中在沿轨迹方向，随着时间变化会产生长期的漂移。径向和法向则呈现出周期变化，严格有界。由于这种不确定性的分布，在集群中仅保证沿轨迹方向的分离距离是无法保证卫星安全性的，可能在随后的轨道中发生碰撞。

因此，集群中两颗卫星，为保证被动安全可以不考虑其沿轨迹方向的相对漂移，仅保证在RN（径法）平面内的安全距离d RNsafe。

1.3 集群的通信保持

集群的通信保持指的是集群中的卫星可获得其他卫星的状态，本文假设集群中的卫星都可以接收或计算出其他卫星的状态。

为了满足通信要求，集群卫星的最大相对距离不能超过设定的通信范围dmax。因此，将以dmax为半径的球作为约束边界。

集群的被动安全和通信要求，可由几何方式表示，如图1 所示。其内外边界分别为以轨迹方向为轴，以投影安全距离d RNsafe为半径的圆柱体外表面和以通信范围dmax为半径的球体内表面。内外边界之间的区域为集群自由飞行区。

图1 集群自由飞行区Fig.1 Free flying region of cluster

2 集群的稳定性与灵活性

稳定性、灵活性是卫星集群的主要性能。本节通过集群成员的状态间转换和集群的漂移等方面来定义和分析集群的稳定性；通过集群的尺度、最优填充和扩展性等问题来定义和分析集群的灵活性。集群的性能结构如图2所示。

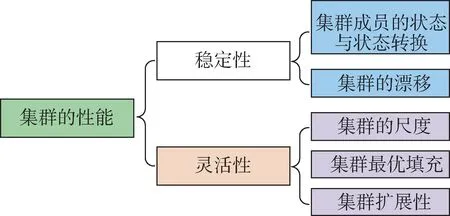
图2 集群的性能Fig.2 Performance of cluster

2.1 集群成员的状态转换

集群状态转换可通过自主模式或地面指令实现，其相互关系如图3所示。

图3 集群成员的状态转换Fig.3 Cluster member state transitions

集群计划是初始状态，集群内保持是一种稳定状态，脱离集群是一种结束状态，集群外围和集群重构为过渡状态。结束状态能够再次循环切换为初始状态。

2.2 集群的漂移

由式（7）可得，卫星相对运动存在两种周期性行为：a）RT（轨道）平面内的椭圆形周期振荡，受到相对偏心率矢量的大小和相位影响；b）垂直于轨道面的法向正弦振荡，受到相对倾角矢量的大小和相位影响。相对轨道要素中α=θ-φ表示相对倾角矢量和相对偏心率矢量的相位差。图4 为典型α值对应的RN平面相对运动。

图4 典型α值对应的RN平面相对运动Fig.4 Relative motion in RN plane for typical α

由图4 可以看出，当α=0°或α=180°时，RN平面的相对运动能够保证一定的相对距离min｛aδe，aδi｝。反之，当α=±90°时，RN平面的相对距离在某些时刻会减小到0，此时卫星沿T向的相对运动也可能在不确定性的影响下减小到一定值，卫星存在碰撞危险。

考虑J2项摄动，α的变化率与轨道倾角有关：

二者关系如图5所示。

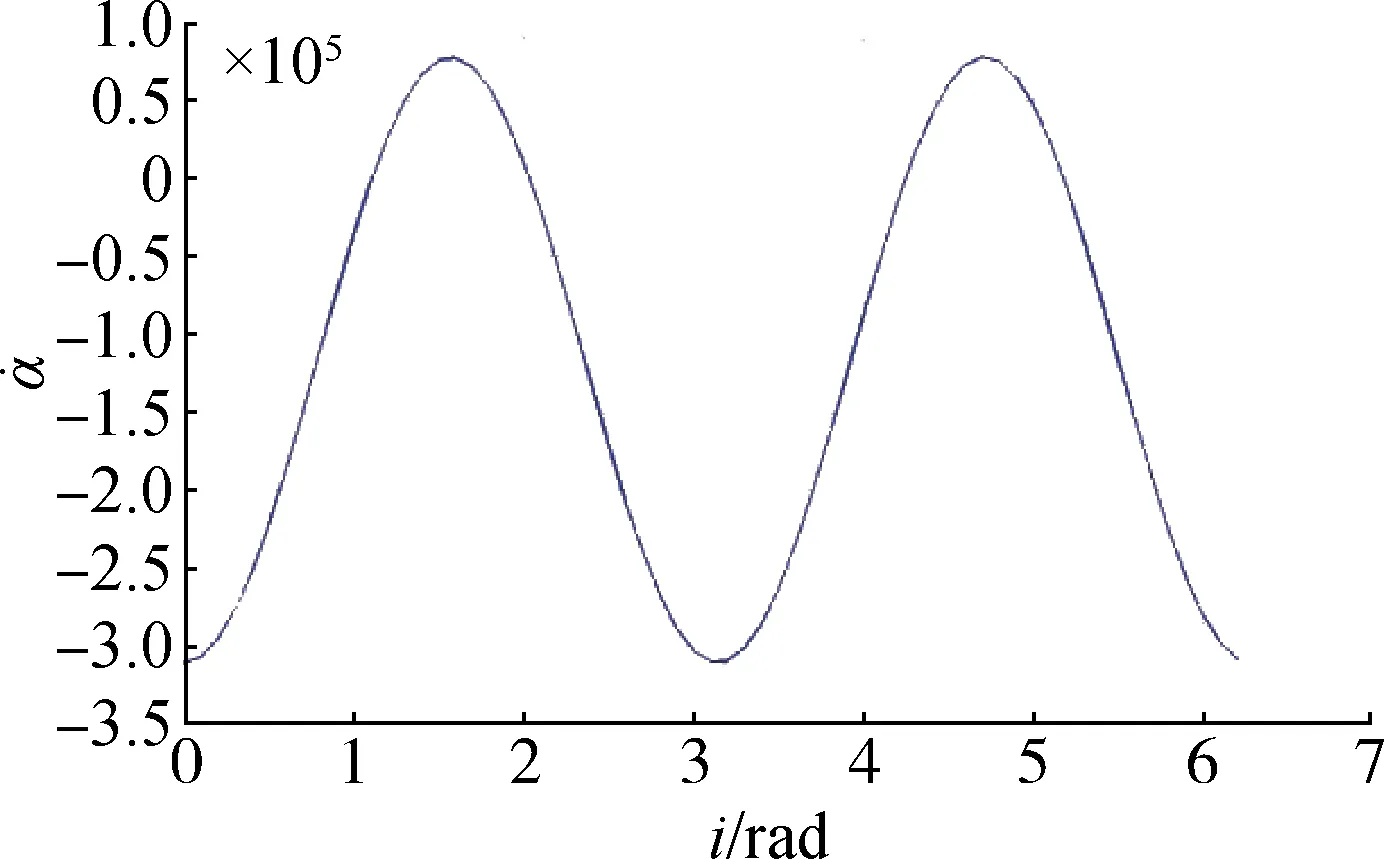
图5 α̇与轨道倾角的关系Fig.5 Relationship between α̇ and inclination

由图5 可得，α的变化率随倾角的变化周期为180°。临界倾角为63.43°和116.57°。在［0°，180°］范围内，当集群卫星的倾角在临界倾角之间时，变化率为正；当集群卫星的倾角在临界倾角以外时，变化率为负。

对于低轨运行的卫星集群，大气阻力摄动影响也非常明显，其切向加速度可表示为［3］

式中ρ为大气密度；β为弹道系数，β=CD(AS/m)，其中CD为大气阻力系数；(AS/m)为面质比。大气阻力差的影响是非周期的。

2.3 集群的尺度

集群的尺度是为了更好地描述集群在空间中相对运动的范围，是衡量集群规模的一种标准。集群尺度根据通信拓扑方式的不同主要分为两类：全局通信拓扑的集群尺度、局部通信拓扑存在有向生成树的集群尺度。本文主要研究全局通信拓扑的集群尺度，即卫星相互之间能够互相传递信息或能量的集群尺度。

对于全局信息拓扑，每个卫星都满足传感器最远通信距离的要求。也就是说，一个集群中相距最远的两个卫星的相对距离不大于传感器的最大通信距离能力dmax。同时，要使卫星之间不产生相互碰撞，距离最近的两个卫星的相对距离不小于卫星的安全距离d RNsafe。在最大通信距离和安全距离之间的空间称为集群飞行区。这样，全局通信拓扑的集群尺度模型就可以简化为一种以虚拟参考卫星为中心的空心球体模型，见图6。

图6 空心球模型Fig.6 Hollow sphere model

使用相对轨道要素描述，dij由式（10）可得：

全局拓扑集群的尺度表示为矢量[RsafeRmax]T。其中，Rsafe和Rmax分别为d RNsafe和dmax的一半，即：

2.4 集群的最优填充

在径法平面内，填充比pr可定义为最大相对距离与径法平面安全距离之比：

通过最小化填充比，可以得到保证被动安全性的最紧密集群状态。

若N个全等圆填充在一个单位圆内，且有N′个全等圆与单位圆相切且两两相切（N′≤N，N′不恒等于N），则最小填充比可由式（13）表示：

当2 ≤N≤9 时，式（13）适用于图7 所示的几种情况。

图7 2 ≤N ≤9，RN平面的最优填充Fig.7 Optimal packing in RN plane for 2 ≤N ≤9

对于N= 10时，不存在N′个既与单位圆相切又与相邻圆相切的全等圆，如图8所示。

图8 N = 10，RN平面的最优填充Fig.8 Optimal packing in RN plane for N = 10

当2 ≤N≤10时，最优填充比如表1所示。

表1 集群的最优填充比Tab.1 Cluster optimal packing ratio

2.5 集群的扩展性

集群的扩展性指的是已有的集群中增加新成员或原有多个集群合并为一个更大规模的集群。

对于不同的初始集群构型，其扩展性不同。如果可在不改变集群构型和原有成员配置的情况下加入新的成员，则集群具有强扩展性；如果需要重新配置原有成员但新成员数量限制较少，则集群具有较强的扩展性；如果需要重新配置原有成员，并且新成员数量有限制，则集群具有较弱的扩展性。对集群的扩展性进行综合仿真分析。

3 综合仿真与分析

3.1 仿真参数设置

为了直观地分析卫星长期集群飞行的性能，设计了4 类初始集群构型，包括：同心环构型、循环构型、同心循环构型、同心交叉构型。4 类集群均包含了8 个卫星成员，轨道倾角设为临界倾角63.43°，轨道高度设为500 km，α设定为0°。4类集群的ROEs分别如表2～5所示。

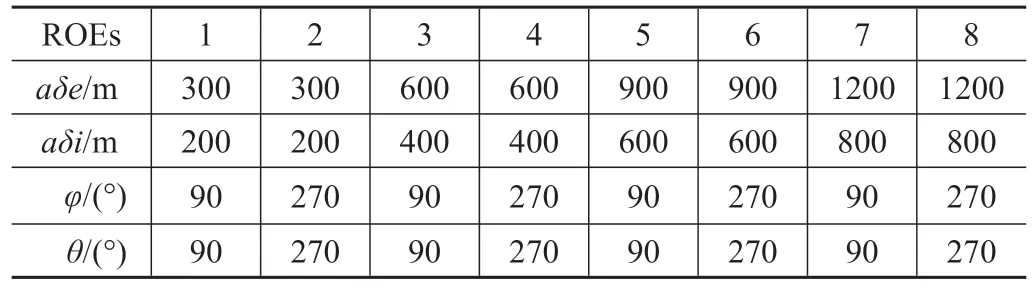
表2 同心环构型的ROEsTab.2 ROEs for concentric ring configuration

表3 循环构型的ROEsTab.3 ROEs for cycle configuration

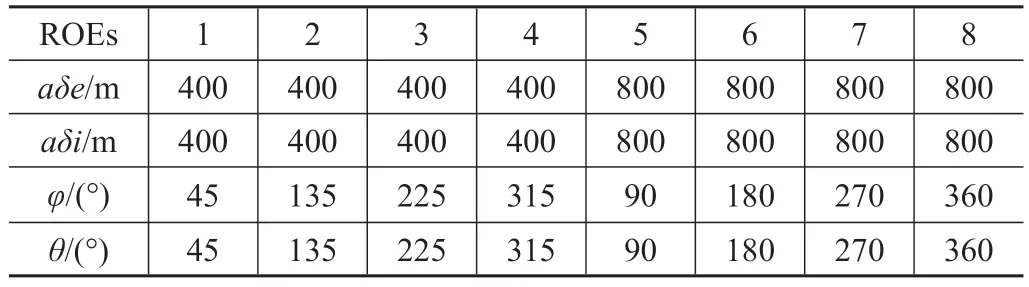
表4 同心循环构型的ROEsTab.4 ROEs for concentric cycle configuration

表5 同心交叉构型的ROEsTab.5 ROEs for concentric cross configuration

3.2 仿真结果与分析

4 种初始集群构型的轨道分别如图9～12 所示，4种类型集群的填充比如图13所示。

图10 8成员集群循环构型Fig.10 Cycle cluster configuration for 8 members

图11 8成员集群同心循环构型Fig.11 Concentric cycle cluster configuration for 8 members

图13 4种类型集群填充比的比较Fig.13 Comparisons of four cluster packing ratio

续图10

由图9～12可得，4类集群均满足集群的安全性和通信要求，在空间中存在简单而有规律的相对运动，且集群均能在J2项摄动的影响下保持稳定。

由图13 可得，同心环构型与同心交叉构型填充比较大，循环构型与同心循环构型填充比较小，且针对8成员集群，同心循环构型的填充比最优。

结合第2.5 节可知，同心环构型下，集群的新成员可以不改变集群构型和配置，具有强扩展性；循环构型下，集群的新成员需重新配置构型，且可扩展的成员数量明显受限，具有较弱扩展性；同心循环构型下，集群可加入新成员的数量比循环构型多，具有较强扩展性；同心交叉构型下，集群的新成员需重新配置集群构型，具有较强扩展性。

4 结束语

本文提出了一种基于相对轨道要素的卫星在轨长期集群飞行稳定性与灵活性分析方法。使用相对轨道要素描述了集群的被动安全和通信保持需求。讨论了集群成员的状态转换、漂移、尺度、最优填充、扩展性等关键性问题，一步步分析了集群飞行的稳定性和灵活性。在数值仿真中，设计了同心环、循环、同心循环、同心交叉4类初始构型，比较了不同构型在稳定性、最优填充、扩展性等指标下的优缺点，为卫星集群飞行的顶层规划、任务分析和工程实践提供了重要理论依据。