非旋转条件下圆柱形底部中心开孔容器中液体的非定常流动特性

陈 湘, 杨铸涛, 王党朝

(内江师范学院 物理与电子信息工程学院, 四川 内江 641100)

0 引言

液体在不同类型的管道容器中因自身重力或外界压力作用下流动,是生产和生活中常见的问题,在诸多大学本科的普通物理教材中都有相类似的讨论,如对圆柱形容器中的液面高度和下降速度、出口处流速等重要物理量进行讨论.但为了直接应用定常理想流体伯努利方程,研究者在模型建立过程中基本上都做了定常流动假设[1-2].在处理实际问题中,因液面下降而引起的非定常流动影响是必须考虑的因素.毛根海[3]在应用流体力学中提出了一种取液面高度微元处理非定常流动的方法.祝洋等[4]用此方法在基于孔口出流模型的研究中,得到结论与定常假设下得到结果相差很大.林建忠等[5]、张兆顺等[6]从欧拉方程出发,推导出了非定常流动的伯努利方程.彭亮滔等[7]通过求解非定常流动的伯努利方程讨论了希罗喷泉的动力学问题.这些研究中所涉及的数学处理方法,对进一步深入研究类似问题提供了重要思路.实际流体问题的处理中,容器形状、器壁阻力、液体类型等因素也会对流动特性造成影响.鲁进利等[8]通过比较相同直径、不同管长的压差,研究了细小圆管内液体流动阻力特性实验研究,结果表明随着管径减小,摩擦因子也减小,且在层流区和湍流区内均要比常规尺度条件下的小.陆向迅等[9]数值模拟的方法,对矩形微通道内液体流动与传热进行了研究,结果表明流体黏度随温度对fRe的影响和黏性耗散对热起始段的作用不能忽略.郝鹏飞等[10]在对粗糙微管道内液体流动特性实验研究中,发现在粗糙单元附近形成的压差阻力是导致流动阻力增加的主要原因,粗糙单元还会引起微管道内的流动失稳,导致粗糙微管道内层流向湍流的转捩点提前.凌智勇等[11]在低黏度液体在微管道中流动特性实验研究中,发现不同长径比对流动特性有一定的影响,在一定条件下出现了明显的尺度效应,管道内壁出现速度滑移致使流量增大.齐红媛[12]采用去离子水和乙醇作为媒介,通过实验和数值模拟的方法研究了在玻璃微通道内的液体流动特性,结果表明材料表面的微观几何形貌以及元素种类均可以改善材料表面的润湿性能.我们前期研究中应用理想流体定常条件下的伯努利方程和连续性方程等,对静止圆柱形容器中非旋转流体沿底部开孔下漏时,液面距底部高度与液面初始高度和时间的关系进行了推导,得到的线性关系结论,其中是一个与圆柱形直径和漏孔直径比值相关的系数.用水做实验的结果很好地验证了上述线性关系,但数据拟合斜率与理论值存在一定的差异[13].这种差异可能来自因液面下降而引起的非定常流动的影响,也可能与液体类型、容器形状、器壁阻力等因素有关,由于只采用了单一液体进行了实验,故未对理论和实验结果差异的原因未做分析.为进一步深入研究上述问题,本文将从流体的欧拉方程出发,首先建立非旋转条件下圆柱形底部中心开孔容器中液体的非定常流动伯努利方程,再结合理想流体的连续性方程,分别采用准定常、非定常近似逼近、精确解析求解等方法,对流动特性进行研究,并结合不同介质的实验结果,进行模型验证和数值分析,以及对准定常解和非定常近似逼近解的关系进行讨论.

1 非定常伯努利方程的导出

1.1 流体力学欧拉描述下的随体导数

流体力学通常有欧拉描述和拉格朗日描述两种描述方式,其中欧拉描述是一种场描述.通过观察流场中固定空间点的流动状况以确定流体质点经过该空间点时的物理量变化规律,即流体质点的任一物理量是空间和时间的函数

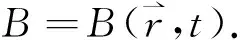
根据质点的踪迹来看,z是时间ε4的函数,因此,在直角坐标系中,物理量c0随时间的变化率为

直角坐标系中速度场为

故有

通过矢量代数的方式可写为不依赖坐标系的形式

1.2 理想流体非定常无旋流动的伯努利方程

通过对流体微元应用牛顿第二定律可以得到流体的运动微分方程,即欧拉方程

容易看出方程左边描述流体微元的运动情况,方程右边描述流体微元的受力情况.

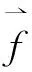
对于欧拉方程,根据随体导数公式

以及矢量代数的运算公式

若液体无黏滞性,则流体微元之间没有摩擦力,仅有正压力,应力张量为对角矩阵

则有

若流场无旋,则有

对上式沿任一瞬时流线L积分

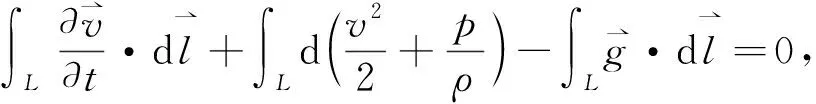
可得不可压缩无黏性流体在重力场下非定常无旋流动的伯努利方程

2 圆柱形底部中心开孔容器中液体无旋下漏的物理模型与求解

2.1 物理模型构建

现有一个直径为D圆柱形容器,底部中心开孔的直径为d.建立如图1所示的坐标,定义圆孔中心处为坐标原点,坐标轴竖直向上,容器内液面高度为z.对于过流截面有限大小的流动即总流,伯努利方程中的动能项应该是所有相同高度质元的平均动能乘上一修正系数,但由于液面是同时下降,总流的伯努利方程等同于流线的伯努利方程.

记液面下降的速度为v,圆孔中心处液体流速为v孔,并将其视为开孔处的速度.因为液体是在面积处处相等的竖直圆柱形容器中同时下降,可视做整个液面以相同的速度v下降,且容易看出液面下降速度是逐渐减小的,所以式(1)中第一项积分可表示为

液体通过圆孔下漏时,在液面和圆孔处的压强p0均与大气压相等.该模型下的非定常流动伯努利方程可化为

同时,根据流体力学中的质量守恒定律即连续性方程

考虑到流体不可压缩,连续性方程可以进一步写为

S孔v孔=S器v,

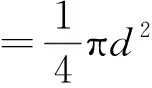
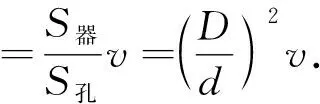
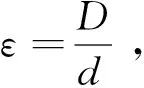
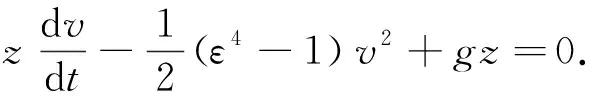
(2)

其定解条件为

2.2 模型在特殊情况下的解析解以及近似解

由于式(2)为二阶非线性变系数非齐次常微分方程,通过常规方法难以求得其一般情况下的通解,本文将采用分类讨论的方式简化方程,以求该方程在特殊情况下的解析解和近似解.

2.2.1 方程在ε=1时的解析解

当ε=1时,非线性项为0,式(2)退化为线性方程

该方程的物理意义是流体的加速度等于重力加速度,而当ε=1时D=d,流体的动力学行为类似于自由落体运动,显然该方程表述的正是这一动力学行为.

通过求解该方程,可以得出与自由落体运动公式相似的两个式子:

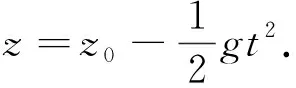
2.2.2 方程在准定常流动下的解

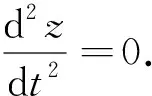
(3)

对该方程分离变量并分别对时间、高度积分,同时考虑定解条件,则有

或

(4)

或

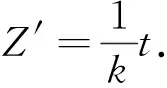
(5)

同时,还可以分别求出液面下降速度和圆孔处液体流出的速度与时间的关系式:

和

由于液面高度下降过程中势必会发生液体流速随时间变化,故在准定常近似下求解的所有关系式均只能在t比较小ε比较大的情况下才成立,t越大或ε越小则误差越大.

2.2.3 逐级逼近法对非定常流动的讨论

如前所述,一般情况下液体流动必然存在非定常性,为使方程的解更加符合实际情况,将使用准定常解逐次代入原方程以逐级逼近非定常流动,准定常解即为零级近似.

将其代入原方程,可以得到

进而可以得到一级近似下的结果:

分离变量并由定解条件积分可以得出一级近似下的液面高度与对应的时间关系:

(6)

t1=βkZ′.

重复上述运算过程,同理可以得出二级近似t2=βt1.根据数学归纳法,容易得出n级近似的表达式

tn=βnkZ′.

同时,对于液面下降速度和圆孔处液体流速,其n级近似为

和

液体流量的n级近似为

对于ε4=2的特殊情况,可以使用数值方法求得方程(2)的数值解,或者通过实验总结出经验公式描述该情况.

2.3 模型的通解讨论

(7)

于是自变量为t、因变量为z的微分式(7)可代换为自变量为z、因变量为v的如下微分方程

(8)

该方程为一阶线性非齐次变系数常微分方程,其通解为对应齐次方程的通解再加上任意一个特解.

v=C1z-w,

式中C1为待定系数.

根据齐次方程通解的形式,可取v=z-wu(z)作为式(8)的试探解,则有

(9)

将式(9)代入式(8)可得

并简化为

分离变量并两边积分可得

最后由v=z-wu(z)可得

(10)

对式(10)进行分离变量积分可得

(11)

可通过以上关系的进一步求解,得到式(2)的通解,其中C、C′为待定系数.

2.4 模型方程的进一步化简

将式(10)代入式(2),可得

记

则方程为如下形式:

若用数学的符号习惯,以x代替t作为自变量,以y代替z作为自变量,且记ε4为一参量c0.则式(2)可写成如下标准式,该式为一个常系数二阶非齐次方程

y″+Ay-c0+B=0.

3 不同径孔比圆形容器中液体无旋下漏的实验研究

3.1 实验研究方法

为验证上述模型的准确性,按照图1进行了实验设计和测量.实验中将外壁标有刻度、高度均为25 cm的不同直径比圆柱形亚克力管置于水平支架上,使用软塞堵住圆孔并灌满低黏度流体.通过高速摄像机记录下液体从容器中下漏的全过程,以液面底部为高度零点,借助计算机图像分析,得到多次测量下液面高度z和对应时间t的平均数据.为避免初始时拔去软塞,以及结束时O点液柱不再连续且液体不能排尽对实验的影响,只取液面高度在24 cm～1 cm范围内的数据.

本文实验研究中所涉及的低黏度液体分别为水,20 ℃时其黏度为1.0 cP;无机溶液饱和盐水,20 ℃时其黏度为2.0 cP;有机溶液75%酒精,20 ℃时其黏度为2.6 cP.

3.2 不同液体水在非旋转下漏的实验结果与讨论

3.2.1 容器内径D不变

按照上述方法,分别测量了容器内径为D=8.60 cm时,圆孔直径d分别为0.80、0.90、1.00、1.10、1.20、1.30、1.40、1.50 cm时,三种液体液面高度z和时间t的测量数据.表1给出了水的具体数据.

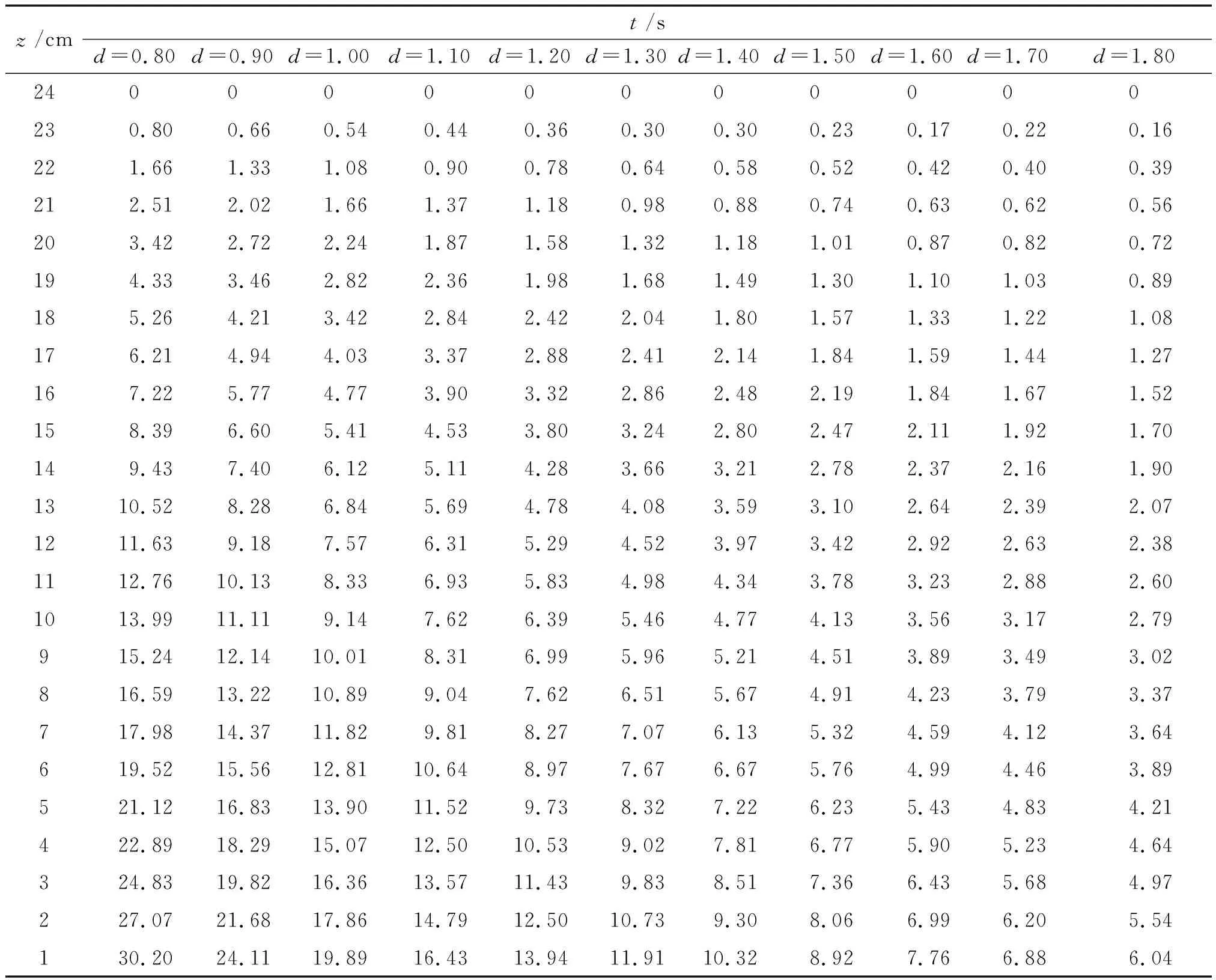
表1 不同液面高度对应的时间

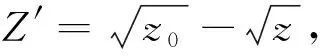
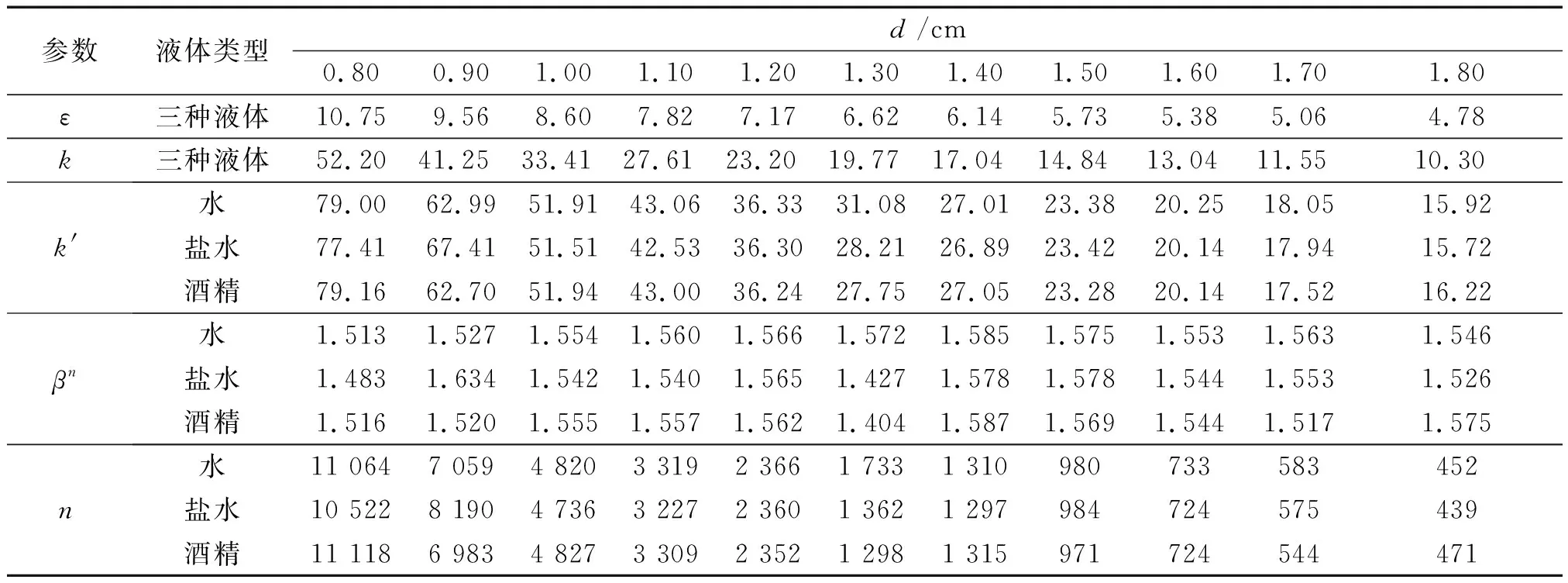
表2 D恒定时不同圆孔直径d情况下相关物理参数

图2 不同圆孔直径d液面折合高度Z′与时间t的关系

根据前面推导的非定常解与准定常解关系tn=k′Z′=βnkZ′=βnt,即βn的值基本在1.5附近微小波动.但由于不同直径比时β的值不同,这意味着在βn的相同的条件下,近似级数n存在较大差异.由表2中的数据进行对数运算logββn得,进而得到近似级数n.可以看出,非定常近似级数n与直径比ε成正相关,但同一直径比下,不同液体的n差异较小.

3.2.2 圆孔直径d不变

采用上述方法,分别测试了圆孔直径d=1.20 cm,容器内径分别为7.60、8.10、8.60、9.10、9.60 cm时三种液体的z和t的数据,表3给出了水的具体值.

表3 不同液面高度对应的时间

同理,根据前述公式可得到相应折合高度.d=1.20 cm时不同直径圆柱形容器中,三种液体下漏过程液面折合高度Z′与对应时间t的关系如图3所示.可以看出,t与Z′各数据点均良好的二者之间线性关系,其形式也与理论解高度吻合.

图3 不同容器内径D液面折合高度Z′与时间t的关系

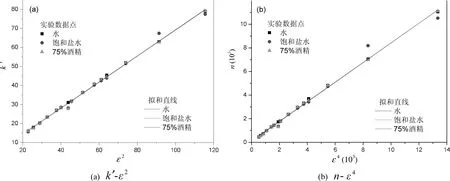
图4 拟合斜率k′和近似级数n随ε变化的关系

同理,对图3直线进行拟合与相关计算,可以得到小孔不变时不同直径比情况下k、k′、βn、n等参数的值,如表4所示.由表4可见,βn的值仍然在1.5附近微小波动,非定常近似级数n与直径比ε成正相关,与容器直径不变情况下的结论一致.

表4 d恒定时不同容器内径D情况下相关物理参数

3.2.3 不同直径比下液体参数对比

经过上述实验,可以发现分别以D和d为单一变量进行实验所得到的结论具有很强的一致性.下面以直径比ε为变量,进一步探究该模型的物理规律.现在将三种不同黏度、不同类型流体实验所得的相关参数与直径比的关系进行进一步的研究与分析.通过实验研究与数据分析,得出了不同溶液在不同直径比容器中下漏时,时间t与折合高度Z′的实际比例k′与近似级数n,具体数据如表5所示.

从表5中容易看出k′、n均与ε成正相关,通过以ε的不同次幂为自变量,k′、n分别作为因变量分别进行线性拟合.斜率k′与ε2和n与ε4关系如图3所示,均呈良好的线性关系.

可以看出,随着液体黏度的增大,k′-ε2线性拟合斜率和n-ε4线性拟合斜率均在对图3进行线性拟合,可以得到对应参数,如表6所示.考虑到流体的流动性随着黏度增大而减小,可定性认为二者随流体黏度增大而减小,但具体的定量关系式还需进一步研究.

由于k′-ε2线性拟合斜率和n-ε4线性拟合斜率随流体黏度的变化率都很小,可以认为使用低黏度流体时k皆为常数,经计算可以得出数值关系的经验公式

k′=0.696ε2和n=0.848ε4.

(12)

t=0.696ε2Z′ .

另外,将经验式(12)代入n级近似的表达式,可以求出k′的另一个表达式

则时间t和液面高度z的关系式可表示为

4 结论