重型吊装场地换填垫层变形计算分析

郝增明, 白晓宇*, 桑松魁, 张明义, 张启军,, 林西伟, 王立彬, 张凯祥, 蔺金龙

(1.青岛理工大学土木工程学院, 青岛 266520; 2.青岛业高建设工程有限公司, 青岛 266042;3.中建八局发展建设有限公司, 青岛 266061; 4.山东恒达信项目管理有限公司, 临沂 276002)

针对重型吊装设备站位所处地基土层较为软弱的问题,采用换填垫层法进行处理是常见措施之一,将站位场地开挖至软弱土层,以高强度、低压缩性的散体材料进行回填,将换填材料分层夯实并找平。该方法的优点是取材方便、机械设备要求低、施工便捷、工期短、节约工程成本,且可以有效减少地基的不均匀沉降。该方法在实际的施工深度需要保持在3.0 m之内,且垫层的厚度也不宜小于0.5 m。

近年来,换填法广泛应用于软弱地基处理中。于瑞文等[1]提出了换土垫层法的地基处理方案,并指出该方法在时间和空间上的优势。文献[2-6]对换填垫层工艺的应用优势、适用范围、铺垫材料的选择开展了相关研究,从经济性对比了常见软基工程中各处理技术,并结合工程特点进行施工质量控制。随着应用日益广泛,垫层设计计算理论也逐渐成熟,孙培芹[7]推导出关于垫层厚度的一元三次方程进而简化为一元二次方程,并指出换填垫层可以调整地基不均匀沉降的结果,使沉降曲线接近于圆周曲线。王炳龙等[8]通过对比换砂法试验和土工格室,提出了试验基础上换填厚度设计容许应力,并为换填厚度设计提供了理论方法。郭秋生等[9]对《建筑地基基础设计规范》(GB 50007—2011)提出异议,通过弹性理论法和扩散角法探讨了垫层的计算厚度,结果表明,弹性理论方法较扩散角法所求得的垫层厚度大。在安全前提下,建议选取造价成本较低的应力扩散角法。针对地基沉降变形的研究,文献[10-12]研究了地基沉降概率分析和可靠度计算方法,并对随机有限元法沉降分析进行了完善。Padilla[13]分析了浅埋地基沉降概率方法,并对沉降概率理论计算进行了系统的梳理。Krizek等[14]基于e-lgp法在多种因素下,对地基沉降的影响展开研究,并将预测沉降和实测沉降的差异进行对比分析。Nishimura等[15]基于比奥固结理论运用Monte-Carlo随机有限元方法进行研究,完善了沉降概率计算理论。通过总结现有的研究成果发现,对于换填垫层场地的计算理论,大多集中在垫层厚度方面,而针对换填垫层后持力层沉降变形计算鲜有研究,亟待进行较为系统的研究。

为完善换填法沉降变形计算理论,对地基不均匀沉降现象进行有效的预防处理[16],现将重点针对青岛市重型吊装场地换填垫层地基持力层的沉降变形展开详细的理论计算分析。并结合现场实测结果,通过ABAQUS有限元模拟分析该场地的沉降量,将模拟结果与修正后分层总和法得到的理论计算沉降结果进行对比验证,以此来判断对沉降经验系数Ψs进行内插法修正的可靠性。同时将斯肯普顿-比伦法中反演弹性模量代入预测模型,验证弹性模量对沉降准确性的影响和该方法的可行性,从而完善相关计算理论。以期使研究结果为类似重型吊装工程的地基处理提供价值参考,对重型设备的稳定性具有重要意义,有效保障人民的生命财产安全。

1 变形计算理论

1.1 总沉降

针对总沉降的计算最常用的方法一般为分层总和法。该方法在计算土中应力时采用弹性理论,假定地基是半无限线性变形体(均质且各向同性)。地基土不产生侧向变形,且变形只发生在有效厚度范围内,并将地基分为若干份,认为整个地基的最终沉降量是各层沉降量之和。最终地基变形量可按《建筑地基基础设计规范》(GB 50007—2011)[17]推荐分层总和法单向压缩的修正公式计算。

基于规范推荐的计算方法,结合现场实际的重型吊装换填场地,先利用应力扩散法计算垫层底部的附加应力,以及扩散后的垫层宽度作为基底,然后采取分层总和法计算持力层的沉降量[18]。

1.2 瞬时沉降

斯肯普顿-比伦法认为饱和黏性土地基最终沉降量s按其成因过程由瞬时沉降sd、固结沉降sc与次固结沉降ss共3个分量组成。

重型吊装开始起吊瞬间,短时间内孔隙水无法排出,土体瞬时产生侧向变形,此时土体体积未发生明显变化。试验表明:土层性质不同,会导致计算方法和弹性模量的取值有较大差异,对于黏性土可利用弹性力学计算公式,弹性模量的取值近似为一个常熟;无黏性土则需利用基础工程中的半经验公式,弹性模量取值相对会复杂,需根据各点的应力水平确定,一般采用有限元等数值解法。

黏性土中基础的瞬时沉降sd,按照式(1)计算。

(1)

式(1)中:μ为土的泊松比,瞬时加载饱和黏性土时由于体积无变化,故取μ=0.5;E为土的弹性模量;ω为各种沉降影响系数,与基础底面形状、基础刚度和计算点的位置有关;b为矩形荷载的宽度或圆形荷载的直径;P0为地基表面均布荷载。

需要说明的是,固结沉降由侧限压缩试验获得,而吊装工程在受荷后,变形与固结仪中单向压缩试验差别很大,所以在此不进行计算处理。次固结沉降因无法进行直观的计算过程,所以在重型吊装换填场地中,采取直接考虑瞬时沉降的方式,从而达到减少变量、简化计算效果。

2 现场试验及结果分析

2.1 土压力现场测试

青岛市一处重型吊装现场[19]地势较平坦,多为丘陵地貌,总体呈现东高西低。换填深度1.5 m,换填材料选用石粉、碎石和毛石,换填土的重度为18 kN/m3,且应力扩散角为30°,地基承载力特征值fak=150 kPa,铺填毛石质量1 245.63 t,走道板质量140 t,起吊设备质量1 679.1 t,吊车质量3 544 t,地下水位为3.5 m。地基处理方式如图1所示,试验场地的地层情况及物理力学参数如表1所示。

表1 试验场地地层物理力学参数

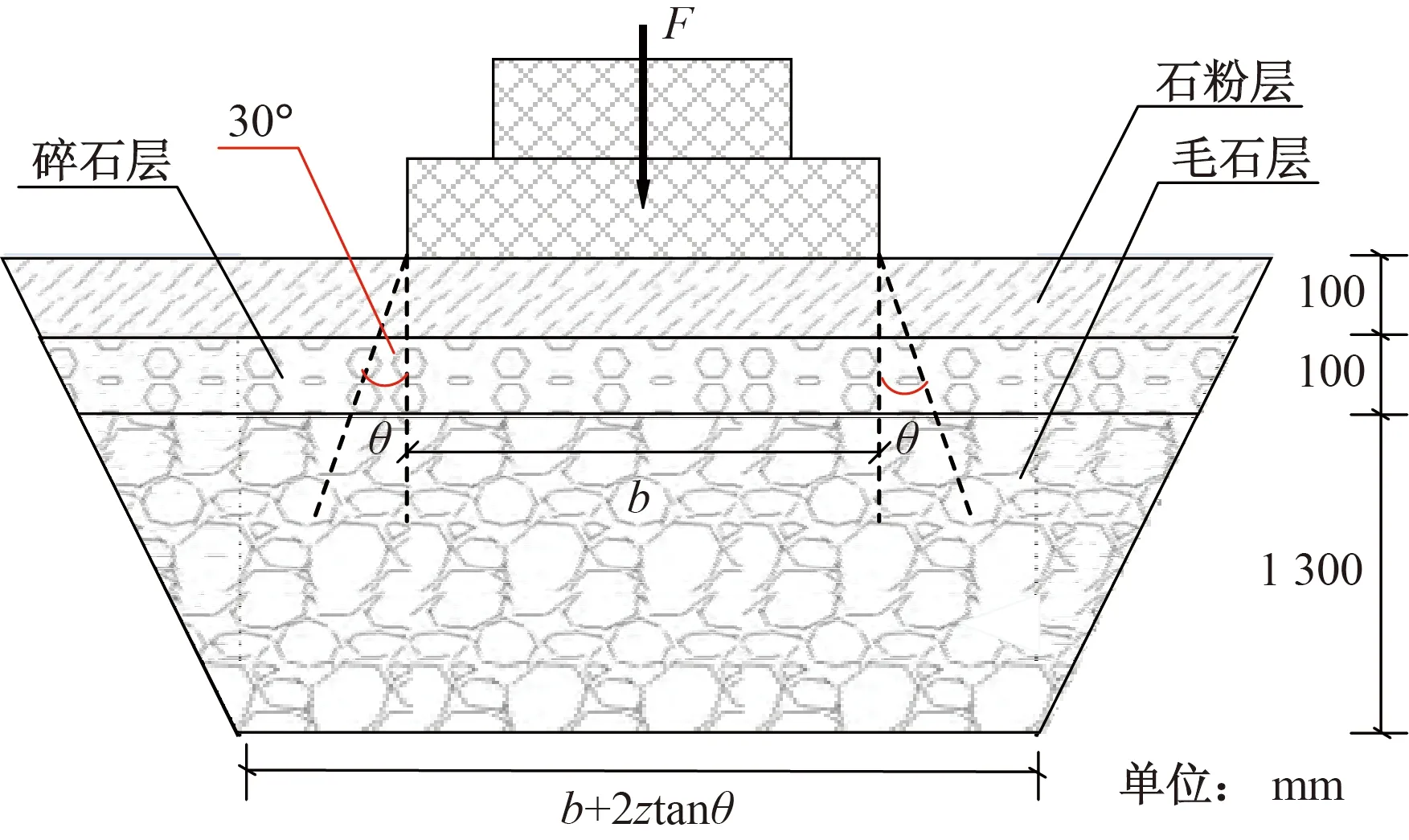
F为施加在换填层表面的荷载质量;θ为垫层应力扩散角;z为垫层的厚度

试验通过现场埋设土压力盒实测XGC88000型4 000 t纯履带式重型吊装场地施工过程中地基土的承压能力,并与正常情况的地基承载力进行对比分析。试验过程:按照施工要求开挖放坡,土压力盒埋放深度1.5 m,水平放置、受力面朝上,吊车中线两侧中间路基箱位置下方各布置3个,且均一个布置于正中,2个在箱边位置,间距为4 m,在两侧路基箱中间应力扩散处布置1个,距箱边866 mm,总计7个土压力盒TY01～TY07。详细土压力测点布置如图2所示。

图2 土压力盒分布图Fig.2 Earth pressure box distribution diagram

土压力盒埋设完毕后,土压力盒读数调零,分层换填石粉、碎石和毛石,压实并找平,垫层施工完成后测试回填荷载压力,记录土压力盒数据[20-21]。然后依次记录吊车在不同工况下土压力盒的读数。不同工况下的测试结果如图3所示。

图3 土压力盒测试结果Fig.3 Earth pressure box test results

从图3可以看出,每个测点的竖向应力随着工况垫层回填完成、吊车组队完成、吊车起钩、设备完全起吊的过程逐渐增加,至吊车回转就位工况出现差异,该工况下仅测点TY02读数有明显增加,其余测点读数与设备完全起吊工况几乎一致。另外,吊车中线两侧的竖向应力出现明显的不对称性,且左侧路基箱明显大于地基承载力特征值150 kPa,说明该重型吊装场地施工过程可能存在地基不均匀变形问题。应力扩散角处的土压力盒TY04呈现出与其他测点明显的不同,竖向应力随工况变化规律虽然一致,但其数值和增幅均偏小。

2.2 总沉降计算

为保障基础上部吊车荷载传递到地基引起的沉降不会对其自身产生不利的影响,假定上部荷载为长期荷载,利用重型吊装换填场地现场试验工况数据,对该试验工程采用分层总和法规范修正公式进行总沉降计算。按规范公式计算可得:走道板铺毛石的面积范围A=415.21 m2,换填层底部的质量W=6 608.73 t,地基持力层表面的压强q=159.2 kPa。

2.2.1 计算地基持力层修正后的承载力

根据《建筑地基基础设计规范》(GB 50007—2011)[17]计算地基持力层修正后的承载力fa=165 kPa,且fa=165 kPa>159.2 kPa,结果表明,重型吊装作业可以正常施工,地基持力层表面的承载力满足要求。

2.2.2 分层总和法的关键参数计算

将位于一条履带下部垫层底面的中点视为沉降计算零点,同时考虑两条履带之间的相互影响,求得分层总和法的关键计算参数,如表2所示。

表2 分层总和法各计算参数

2.2.3 计算各分层的沉降量

将表2中各参数代入《建筑地基基础设计规范》(GB 50007—2011)[17]分层总和法单向压缩的修正公式进行计算,求得各层沉降量结果如表3所示。并确定地基变形计算深度zn=11.6 m,故地基变形计算深度范围内总沉降量s′=186.1 mm。

表3 各分层沉降量

2.2.4 沉降计算经验系数Ψs计算

沉降计算经验系数Ψs按《建筑地基基础设计规范》(GB 50007—2011)[17]进行取值。

2.2.5 内插法修正沉降计算经验系数Ψs

(2)

该计算理论下,重型吊装场地换填垫层后持力层最终总沉降量为243.0 mm,在规范的容许值之内,满足高耸结构物地基沉降量的要求。

2.3 瞬时沉降计算

求解瞬时变形时,可以利用换填垫层检测时的静载试验,记录各级荷载作用下的地基变形量[22],并将静载试验载荷板沉降量假定为试验工况下将要发生的沉降,利用沉降值进行反算,解决地基弹性模量难以准确确定的难题,该方法虽比短时荷载时间要长,但是其试验前一两级与吊装作业的时间一致,证明该地基的弹性模量可以通过静载试验测的沉降值进行反演。

静载试验,分10级加荷,每级加荷后持荷2 h,每小时内沉降量不超过0.1 mm,即认为达到稳定状态,可以进行下一级加载。且每级加荷后记录载荷板沉降值,得到荷载-位移曲线如图4所示。

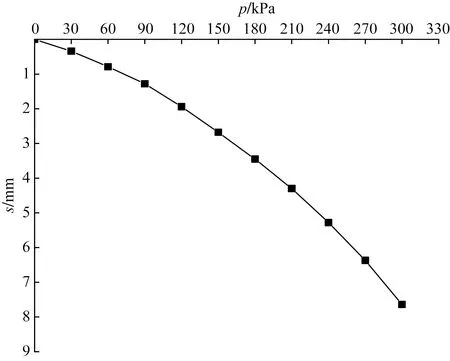
图4 p-s曲线Fig.4 p-s curve

图4显示,p-s曲线变化规律大致分3个阶段,第1阶段:p-s曲线几乎呈直线状态,证明加荷前期土体中剪应力未达到该场地土的抗剪强度。第2阶段:随着荷载的增加曲线中各点的斜率逐渐增大,沉降量增幅也随之增加,此时加载已超过吊装实际荷载。第3阶段:增加相同的荷载,沉降量增加明显变大,说明换填垫层增加较小的荷载,便会产生较大的变形;且荷载加至300 kPa时,瞬时荷载下累计沉降量为7.64 mm,此结果远小于假定在长期荷载作用下优化分层总和法计算所得地基最终沉降量243.0 mm,因此,通过试验可以建议:规范应降低地基变形量的要求。

根据静载试验沉降量的实测结果,代入瞬时沉降[式(1)]中,分别针对以下两种不同情况进行反演弹性模量:①将换填垫层视为地基,重型吊装为上部直接荷载,反算可得到换填垫层与地基弹性模量当量值(也可认为是综合弹性模量);②将换填垫层作为原有上部结构的延伸体,即认为换填垫层是上部结构的一部分[23],荷载换算为持力层表面的荷载,反演得到持力层的综合模量。

图5显示,随着静载试验中荷载的逐级增加,反算的弹性模量E1和E2逐渐减小,且存在E1≈3E2的关系,说明重型吊装场地下,吊装时间越长,相应的弹性模量也就越小。E1在180 kPa时存在明显的突增现象。分析原因,大概率为试验测量误差导致,为非正常变化规律。将换填垫层视为上部结构的延伸体,反算得到的E2与勘察报告中给出的Es存在明显的数量级差异。且试验反演得到的弹性模量,可以为相似地质条件下的吊装作业工程提供参考,根据具体施工作业时间,选择相应的反演模量。

图5 p-E曲线Fig.5 p-E curve

3 有限元模拟分析

针对青岛市一处重型吊装场地换填垫层的沉降量采用ABAQUS有限元软件进行分析验证,将模拟的沉降结果与总沉降计算结果进行对比,证明其结果的准确性,并将瞬时沉降反演得到的垫层与地基土综合模量代入模型,与试验结果进行对比验证。基于近年来国内外学者提出的众多经典岩土本构模型[24-25],经对比分析选用适合换填垫层材料的M-C模型。二维模型[26]选择建立在受力与沉降较大,与吊车履带方向垂直的中间位置截面。模型尺寸取吊车横向60 m,深度30 m,垫层厚度与试验尺寸一致,厚1.5 m。表4为换填垫层的主要模型参数。

表4 换填垫层参数

试验场地原位土层参数见表1,弹性模量为45 MPa,泊松比为0.2,重度为18 kN/m3。网格划分时,控制网格属性为四面体,利用结构划分技术进行网格划分,地基土采用T3D2实体单元,毛石垫层设为C3D8实体单元,二节点二维框架,尺寸为60 m×30 m,网格数为1 800。由于换填垫层的尺寸与总尺寸相比较小,且应力扩散较简单,故不进行加密网格划分,模型网格划分如图6所示。

图6 模型网格划分Fig.6 Model grid division

考虑地基土自重,设一个地应力分析步。模型底部设有固定铰支座,左右两侧设位移边界,限制其水平方向发生位移,上部为自由端,加荷区域距吊车中线3.2～11.2 m的范围,设置左右两处均布荷载,大小为160 kPa,模型边界与上部附加应力如图7所示。有限元分析时,持力层视为理想弹塑性体,采用莫尔-库伦屈服准则和相关联流动法则。

图7 模型边界与上部附加应力Fig.7 Model boundary and upper additional stress

基于平衡条件及屈服条件,采用初始地应力平衡方法,将重力荷载施加于换填垫层和持力层土体,水位以下考虑浮力影响,根据工程情况定义边界条件,运算得出初始应力场,将重力荷载和边界条件同时施加于模型中,得到不违背屈服准则的初始地应力平衡模型,如图8和图9所示。

图8 模型初始应力场Fig.8 Model initial stress field

图9 地应力平衡竖向压应力云图Fig.9 Ground stress equilibrium vertical compressive stress cloud

将换填垫层底面和持力层土体定义为摩擦界面,垫层两侧的超载可约束下方土体产生水平位移[27],并考虑影响摩擦力作用的多种因素[28]。利用初始地应力平衡的手段,将荷载施加于垫层和持力层,地下水位以下土体考虑浮力影响。将边界条件和重力荷载同时施加于所建模型中,最终得出该工况下的竖向变形,如图10所示。

图10 重型吊装工况竖向变形Fig.10 Vertical deformation of heavy lifting condition

图10显示,地基土的竖向位移随深度增加呈逐渐减小的趋势。在吊车中心线左右各3 m范围内未施加荷载情况下,该处的垫层和较浅处地基土也产生了变形,但与两侧相比较小,该处变形是由于深层土的变形所致,且在吊车中线处并非最上方竖向位移增幅最大。模拟计算的沉降值为244.0 mm,与修正后分层总和法计算所得的243.0 mm非常吻合,进一步验证了内插法修正沉降计算经验系数的可靠性。再将瞬时沉降反算所得的垫层与地基土综合模量E1代入重型吊装场地换填垫层的预测模型中,模拟瞬时荷载下的变形如图11所示。

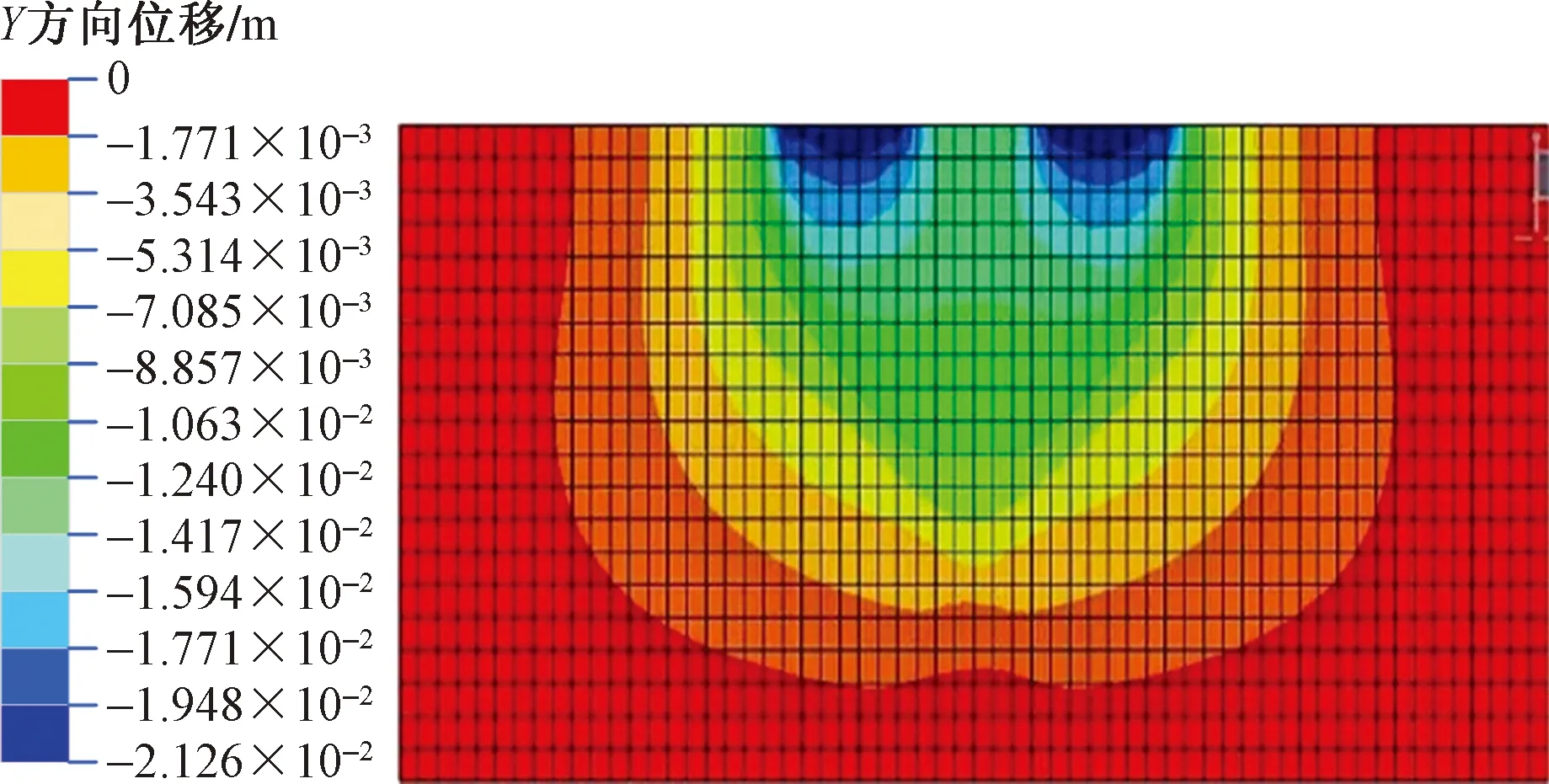
图11 预测模型竖向位移云图Fig.11 Vertical displacement nephogram of prediction model

通过对比图10、图11可知,弹性模量对地基土的变形影响较大,且反算得到垫层与地基土综合模量可以使地基变形计算结果更加准确,模拟结果与静载试验实测结果更加接近,同样证明了该方法的实用性,验证了该方法反演的弹性模量可以对其他类似吊装工程换填垫层场地提供参考和借鉴。结合图3土压力盒测试结果,发现吊车中线左右3 m范围内,应力和位移都较小,说明该处的换填垫层并没有发挥应有的作用,后续工程可以对该范围内换填垫层进行进一步优化。

4 结论

(1)利用内插法对分层总和法规范修正公式中的沉降计算经验系数Ψs进行修正,可以使吊装工程中地基最终变形量由241.9 mm修正为243.0 mm,修正结果与数值模拟中的沉降值244.0 mm较为吻合,证实了该优化方法的可行性。

(2)对比瞬时沉降中静载试验和模拟结果,论证了弹性模量的反演值准确性较高,可以根据施工作业时间,选择相应的弹性模量。通过荷载与弹性模量反演值的关系曲线发现,弹性模量反演值存在E1≈3E2的关系。

(3)试验条件下,0～2 m沉降量为22.9 mm,2～4 m沉降量为32.8 mm,垫层和较浅处地基土变形反而相对较小,进一步证明了换填垫层在重型吊装场地的实用性。

(4)在吊车中线左右3 m范围内地基土的应力和变形均比两侧履带处小很多,表明该范围内换填垫层并未发挥应有的作用,建议工程中对该区域内的垫层进行合理优化,节约造价,缩短工期。